6.1因式分解[下学期]
图片预览




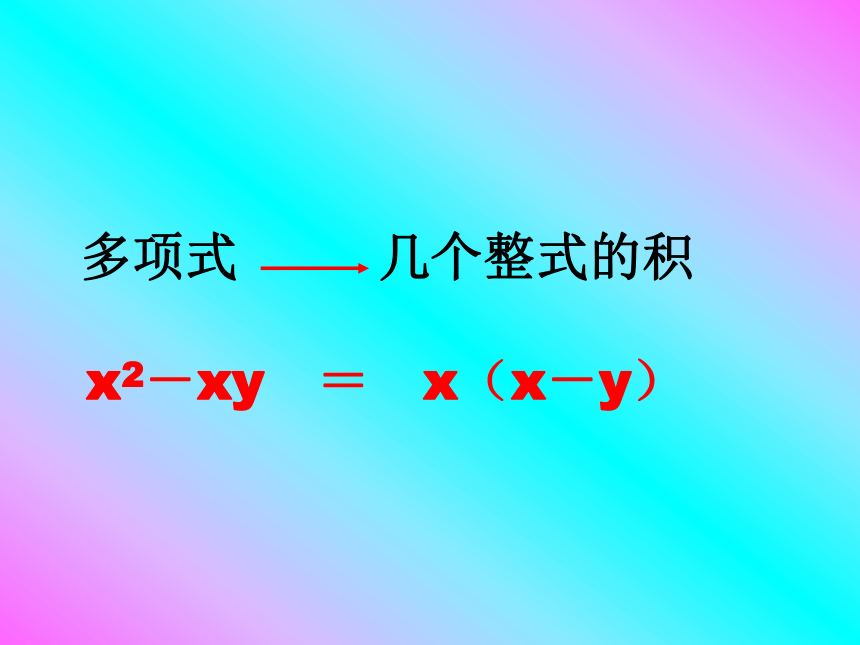


文档简介
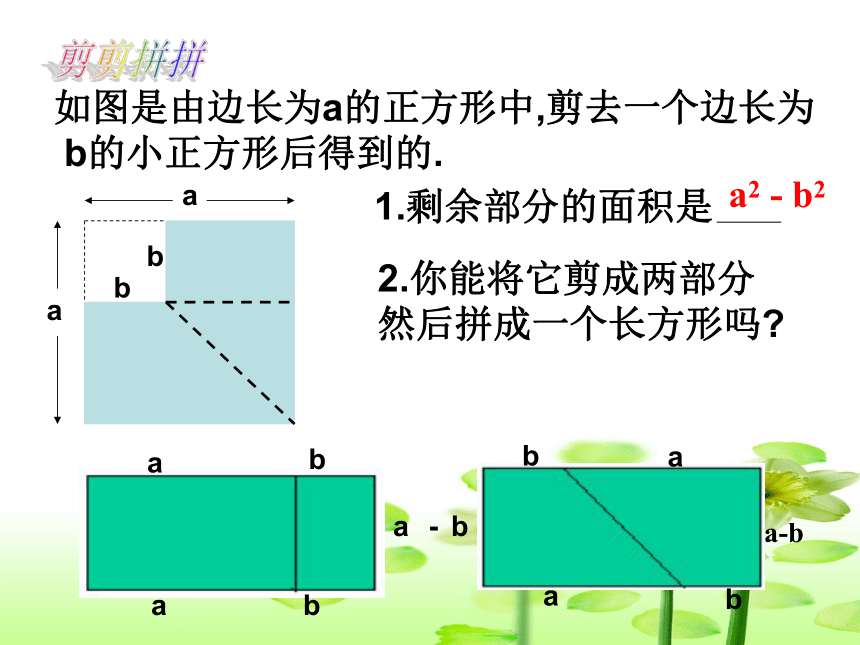
课件25张PPT。6.1因式分解浙教版七年级下册 如图是由边长为a的正方形中,剪去一个边长为
b的小正方形后得到的.aabb2.你能将它剪成两部分然后拼成一个长方形吗?剪剪拼拼a2 - b2 如图是由边长为a的正方形中,剪去一个边长为
b的小正方形后得到的.aabb2.你能将它剪成两部分然后拼成一个长方形吗?剪剪拼拼a2 - b2 如图是由边长为a的正方形中,剪去一个边长为
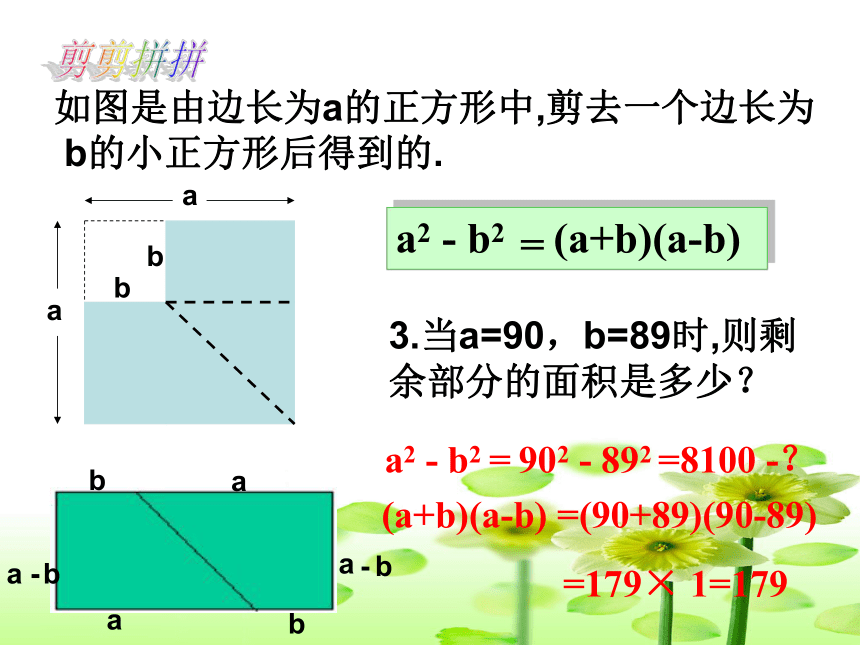
b的小正方形后得到的.aabba2 - b2剪剪拼拼3.当a=90,b=89时,则剩余部分的面积是多少?aaaabbbb--a2 - b2 = 902 - 892 =8100 -?
(a+b)(a-b) =(90+89)(90-89)
=179× 1=179(a+b)(a-b)=a2-b2=(a+b)(a-b)=(a+b)2=m(a+b)(a+b)(a-b)(a+b)2m(a+b)=a2-b2=a2+2ab+b2 =am+bm整式的积多项式多项式整式的积a2+2ab+b2am+bm 合作交流,探索新知 一般地,把一个多项式转化成几个整式的积的形式,叫做因式分解,有时我们也把这一过程叫做分解因式。 多项式几个整式的积x2-xy = x(x-y)辨一辨(1)(2)(3)(4)(5)(6)(7)是不是是不是不是不是不是下列从左到右的变形是因式分解吗?(8)是想一想因式分解与整式乘法有什么关系?因式分解与整式乘法是互逆 过程你能否根据这个关系先写出整式相乘的例子,并由此得到相应的两个多项式的因式分解吗? (1)∵3a(a+4) =3a2+12a
∴ 3a2+12a = ( )( );
(2)∵ (a+3)2=a2+6a+9
∴a2+6a+9 = ( )( );
(3)∵(2-a)(2+a) = 4-a2
∴4-a2 = ( )( ); 填空3aa+4a+3a+32-a2+a (a+3)2例:检验下列因式分解是否正确? (1) x2 y-xy 2=xy(x-y)(2) 2x2-1=(2x+1)(2x-1)(3) x2+3x+2=(x+1)(x+2)用什么方法检验
因式分解是否
正确呢?看等式右边几个
整式相乘的积与
左边的多项式是
否相等例1:检验下列因式分解是否正确
(1)x2 y-xy2 =xy(x-y)
(2) 2x2 –1=(2x+1)(2x – 1)
(3) x2 +3x+2=(x+1)(x+2)
(3) ∵ (x+1)(x+2)=x2 +3x+2 = x2 +3x+2
∴因式分解x2 +3x+2=(x+1)(x+2)正确
解(1)∵ xy(x-y)= xy?x- xy?y= x2 y-xy2
∴ 因式分解x2 y-xy2 =xy(x-y)正确
(2) ∵(2x+1)(2x – 1)=4x2 -1≠ 2x2 –1
∴因式分解2x2 –1=(2x+1)(2x – 1)不正确例:检验下列因式分解是否正确:
(1)m2+mn = m(m+n)
(2)a2-b2 = (a+b)(a-b)
(3)x2-x-2 = (x+2)(x-1)做一做:问题1:
你能利用上面的等式快速计算 1012 — 992=? 解: 1012 — 992
= (101+99)(101 — 99)
= 400问题2: 872+87×13 又该怎么算呢?解: 872+87×13=87×(87+13)=87×100=8700利用a2+ab=a(a+b)课堂聚焦收获季节.规律总结分解因式与整式乘法是互逆过程.
分解因式要注意以下几点:
1.分解的对象必须是多项式.
2.分解的结果一定是几个整式的乘积的形式.
3.要分解到不能分解为止.比一比 赛一赛把左?右两个相等的代数式用线连接起来2a2-2aa2+6a+94-a23a2+12a(2-a)(2+a)2a(a-1)(a+3)23a(a+4)想一想?如果2x2+mx-2可分解因式为
(2x+1)(x-2),求m的值解:由题意得: 2x2+mx-2= (2x+1)(x-2)
∵ 2x2+mx-2=2x2-3x-2∴对应项的系数相等则m=-3会了吗? 请试一试若能x2+ax+b分解成(x+3)(x+4),求a,b的值 如图是由2个边长分别为100和99的正方形重叠得到的.求图中蓝色部分的面积.…探索求新:图中若由100个边长分别为100,99,98,…,2,1的正方形重叠而成的,那么,按这种方式重叠而成的蓝色部分面积是________. 1002 –992 + 982- 972 +
962-952 +…+ 22-12
( ) ( )
( ) ( )=(100+99)(100-99)+(98+97)(98-97)
+(96+95)(96-95)+…+(2+1)(2-1)
=100+99+98+97+96+95+…+1=50505050作业作业本(2) 利用整式乘法与因式分解的关 系写出两条因式分解的式子温馨提示:作业本29页T1应改为:
∵-2a(a-2)=-2a2+4a
∴ -2a2+4a=______________练习提高 拓展应用 1. 计算: 7652×17-2352 ×17
解: 7652×17-2352 ×17
=17(7652 -2352)=17(765+235)(765 -235)
=17 ×1000 ×530=9010000 2. 20042+2004能被2005整除吗?
解: ∵20042+2004=2004(2004+1)
=2004 ×2005
∴ 20042+2004能被2005整除(2)-7-10800cm2 课外同步,延伸提高探究活动再 见
b的小正方形后得到的.aabb2.你能将它剪成两部分然后拼成一个长方形吗?剪剪拼拼a2 - b2 如图是由边长为a的正方形中,剪去一个边长为
b的小正方形后得到的.aabb2.你能将它剪成两部分然后拼成一个长方形吗?剪剪拼拼a2 - b2 如图是由边长为a的正方形中,剪去一个边长为
b的小正方形后得到的.aabba2 - b2剪剪拼拼3.当a=90,b=89时,则剩余部分的面积是多少?aaaabbbb--a2 - b2 = 902 - 892 =8100 -?
(a+b)(a-b) =(90+89)(90-89)
=179× 1=179(a+b)(a-b)=a2-b2=(a+b)(a-b)=(a+b)2=m(a+b)(a+b)(a-b)(a+b)2m(a+b)=a2-b2=a2+2ab+b2 =am+bm整式的积多项式多项式整式的积a2+2ab+b2am+bm 合作交流,探索新知 一般地,把一个多项式转化成几个整式的积的形式,叫做因式分解,有时我们也把这一过程叫做分解因式。 多项式几个整式的积x2-xy = x(x-y)辨一辨(1)(2)(3)(4)(5)(6)(7)是不是是不是不是不是不是下列从左到右的变形是因式分解吗?(8)是想一想因式分解与整式乘法有什么关系?因式分解与整式乘法是互逆 过程你能否根据这个关系先写出整式相乘的例子,并由此得到相应的两个多项式的因式分解吗? (1)∵3a(a+4) =3a2+12a
∴ 3a2+12a = ( )( );
(2)∵ (a+3)2=a2+6a+9
∴a2+6a+9 = ( )( );
(3)∵(2-a)(2+a) = 4-a2
∴4-a2 = ( )( ); 填空3aa+4a+3a+32-a2+a (a+3)2例:检验下列因式分解是否正确? (1) x2 y-xy 2=xy(x-y)(2) 2x2-1=(2x+1)(2x-1)(3) x2+3x+2=(x+1)(x+2)用什么方法检验
因式分解是否
正确呢?看等式右边几个
整式相乘的积与
左边的多项式是
否相等例1:检验下列因式分解是否正确
(1)x2 y-xy2 =xy(x-y)
(2) 2x2 –1=(2x+1)(2x – 1)
(3) x2 +3x+2=(x+1)(x+2)
(3) ∵ (x+1)(x+2)=x2 +3x+2 = x2 +3x+2
∴因式分解x2 +3x+2=(x+1)(x+2)正确
解(1)∵ xy(x-y)= xy?x- xy?y= x2 y-xy2
∴ 因式分解x2 y-xy2 =xy(x-y)正确
(2) ∵(2x+1)(2x – 1)=4x2 -1≠ 2x2 –1
∴因式分解2x2 –1=(2x+1)(2x – 1)不正确例:检验下列因式分解是否正确:
(1)m2+mn = m(m+n)
(2)a2-b2 = (a+b)(a-b)
(3)x2-x-2 = (x+2)(x-1)做一做:问题1:
你能利用上面的等式快速计算 1012 — 992=? 解: 1012 — 992
= (101+99)(101 — 99)
= 400问题2: 872+87×13 又该怎么算呢?解: 872+87×13=87×(87+13)=87×100=8700利用a2+ab=a(a+b)课堂聚焦收获季节.规律总结分解因式与整式乘法是互逆过程.
分解因式要注意以下几点:
1.分解的对象必须是多项式.
2.分解的结果一定是几个整式的乘积的形式.
3.要分解到不能分解为止.比一比 赛一赛把左?右两个相等的代数式用线连接起来2a2-2aa2+6a+94-a23a2+12a(2-a)(2+a)2a(a-1)(a+3)23a(a+4)想一想?如果2x2+mx-2可分解因式为
(2x+1)(x-2),求m的值解:由题意得: 2x2+mx-2= (2x+1)(x-2)
∵ 2x2+mx-2=2x2-3x-2∴对应项的系数相等则m=-3会了吗? 请试一试若能x2+ax+b分解成(x+3)(x+4),求a,b的值 如图是由2个边长分别为100和99的正方形重叠得到的.求图中蓝色部分的面积.…探索求新:图中若由100个边长分别为100,99,98,…,2,1的正方形重叠而成的,那么,按这种方式重叠而成的蓝色部分面积是________. 1002 –992 + 982- 972 +
962-952 +…+ 22-12
( ) ( )
( ) ( )=(100+99)(100-99)+(98+97)(98-97)
+(96+95)(96-95)+…+(2+1)(2-1)
=100+99+98+97+96+95+…+1=50505050作业作业本(2) 利用整式乘法与因式分解的关 系写出两条因式分解的式子温馨提示:作业本29页T1应改为:
∵-2a(a-2)=-2a2+4a
∴ -2a2+4a=______________练习提高 拓展应用 1. 计算: 7652×17-2352 ×17
解: 7652×17-2352 ×17
=17(7652 -2352)=17(765+235)(765 -235)
=17 ×1000 ×530=9010000 2. 20042+2004能被2005整除吗?
解: ∵20042+2004=2004(2004+1)
=2004 ×2005
∴ 20042+2004能被2005整除(2)-7-10800cm2 课外同步,延伸提高探究活动再 见
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
