5.4乘法公式[下学期]

课件16张PPT。5.4 乘法公式
-平方差公式多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.知识回顾2.计算下列各题:
(1) (a +b)( a-b )=? (2) (a+2)(a-2)=?
(3) (3-x)(3+x)=? (4) (2m+n)(2m-n)=?(a + n )(b + m)= ab +am + nb +nm.1.多项式与多项式相乘的法则:由此,我们可以得到什么结论呢?
平方差公式:(a + b )(a - b)=a2-b2这里的字母a，b可以是数，或是单项式，甚至是更复杂的代数式即两数和与这两数差的积等于这两个数的平方差.1.计算（口答）：
（1）（x+1)(x-1)
(2) (x+2)(x-2)
(3) (-m+n)(-m-n)
(4) (m+6)(m-6)
(5) (x+2y)(x-2y)
(6) (3x-2)(3x+2)
(7) (b+5a)(b-5a) = x2-1=(-m)2-n2=x2-(2y)2=x2-4y2=m2 - 6 2 = m2-36=(3x)2-22=9x2-4= X2 - 4= b2 - (5 a )2 =b2 - 25a 2 =m2-n2
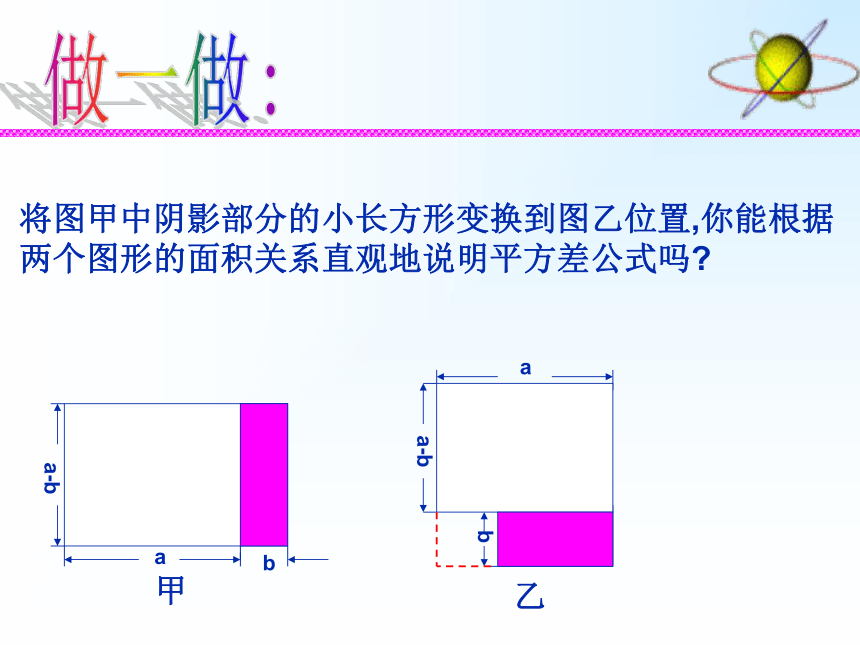
将图甲中阴影部分的小长方形变换到图乙位置,你能根据两个图形的面积关系直观地说明平方差公式吗?
a-babba-ba甲乙做一做:下列式子中哪些可以用平方差公式运算?
⑴ (ab-8)(ab+8) ⑵⑶ (2+a)(a-2) ⑷ (3a+2b)(3a-2b)
⑸ (-4k+3)(-4k-3) ⑹ (1-x)(-x-1)
⑺ (-x-1)(x+1) ⑻ (x+3)(x-2)
加油哦！！明察秋毫(1)(3x+5y)(3x-5y) 　 自主尝试⑶ (2+a)(a-2) 1.使用平方差公式(a+b)(a-b)=a2-b2 时，关键在于找准___与___，公式左边积的两个因式中相同的项看作a，互为相反数的项中带正号的项看作b。
如：(2x+3y)(3y-2x)中，____看作a,____看作b.小结ab3y2x 1. 运用平方差公式计算: 2 . 用平方差公式计算:
(1)103×97 (2)59.8×60.2继续探究(5)992 - 1××××判断正误：（1）(2b+a)(a-2b)=4b2 -a2 ( ) （2）(m–n )(-m -n)=-m2 -n2 ( ) （3）(x+ y) (-x -y)=x2 -y2 ( ) （4）(2a+b)(a-2b)=2a2- 2b2 ( ) n2 -m2a2 -4b22a2- 3ab-2b2
-x2-2xy -y2展示风采
第一关１．已知x2-y2=8，x-y=4，求x+y的值。
２．有两个正方形的周长之和为36cm，面积之差为72cm2,你能求出这两个正方形的边长吗？
第二关祝你成功！4×65×57×98×811×1312×12观察并计算下列各组算式从以上的过程中你发现了什么规律？请用字母表示这一规律，你能说明它的正确性吗？=24=25=63=64=143=144
加油哦！！
第三关挑战极限1.当x=2时,求x(4x+3)-(2x+1)(2x-1)的值．2.如果A=1234567892,
B=123456788×123456790,
试比较A与B的大小.运用平方差公式计算: 5678×5680-56792=(5679-1)(5679+1)-56792=56792 -1 -56792= -1 (2+1)(22+1)(24+1)(28+1)+1=(2-1)(2+1)(22+1)(24+1)(28+1)+1=(22-1)(22+1)(24+1)(28+1)+1=(24-1)(24+1)(28+1)+1=(28-1)(28+1)+1=216-1+1=216 一养鸡专业户改建一个边长为 a(m)的正方形养鸡场,计划纵向扩大3m,横向缩短3m,改建为长方形养鸡场.问改建后的养鸡场面积有没有变化?如果有变化,变化多少?原正方形的面积= a2
改建后的长方形的面积= (a+3)(a-3)=a2-9 (a+3)(a-3)-a2 = a2 -9-a2 =9
1.平方差公式:(a+b)(a-b)=a2-b2
两数和与这两数差的积等于这两数的平方差.2.学会运用平方差公式进行计算.谈谈今天你的收获？再见