2022-2023学年浙教版七年级下第3章 整式的乘除 单元检测卷(2)(含解析)
文档属性
| 名称 | 2022-2023学年浙教版七年级下第3章 整式的乘除 单元检测卷(2)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 535.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 16:02:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2022-2023学年浙教版七年级下第3章 整式的乘除 单元检测卷(2)
一.选择题(共10小题,每小题3分,共30分)
1.下列计算正确的有:①(﹣1)0=1;②;③(﹣x3)m=(﹣xm)3;④;⑤(a﹣3b)(﹣3b﹣a)=a2﹣9b2.( )
A.4个 B.3个 C.2个 D.1个
2.利用完全平方公式计算(﹣s2+t)2应等于( )
A.﹣s2﹣2st+t2 B.﹣s4﹣2s2t+t2 C.s4﹣2s2t+t2 D.s4﹣2st﹣t2
3.若(x+a)(x﹣5)=x2+bx﹣10,则ab﹣a+b的值是( )
A.﹣11 B.﹣7 C.﹣6 D.﹣55
4.已知(x+y)2=49,(x﹣y)2=25,则xy=( )
A.﹣6 B.6 C.12 D.24
5.已知关于x的多项式ax﹣b与3x2+x+2的乘积展开式中不含x的二次项,且一次项系数为﹣5,则ab的值为( )
A.﹣ B. C.﹣3 D.3
6.如图,4张长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2.若S1=2S2,则a、b满足( )
A.a=3b B.a=2b C.2a=5b D.2a=3b
7.2×(3+1)(32+1)(34+1)(38+1)(316+1)+1的计算结果是( )
A.332+1 B.332﹣1 C.331 D.332
8.若4x2+1加上一个单项式后能成为一个多项式的完全平方式,则这个单项式可能就是下列单项式:①﹣1;②﹣4x2;③4x4;④4x;⑤﹣4x中的( )
A.①②③④⑤ B.③④⑤ C.①②④⑤ D.②③④⑤
9.已知(x﹣2020)2+(x﹣2022)2=18,则(x﹣2021)2的值是( )
A.4 B.8 C.12 D.16
10.如图,方形网格能验证下列哪个选项中的等式成立( )
A.(a+b+c)2=a2+b2+c2 B.(a+b+c)2=a2+b2+c2+2abc
C.(a+b+c)2=a2+b2+c2+ab+bc+ac D.(a+b+c)2=a2+b2+c2+2ab+2bc+2ac
二.填空题(共6小题,每小题4分,共24分)
11.现有以下几个算式:
(1)(0.5﹣)0=1;(2)﹣x (﹣x)6=x7;(3)(﹣a2)3=a6;(4)(b﹣a)2=b2﹣ab+a2;(5)(﹣a﹣2b)(a﹣2b)=﹣a2+4b2;(6)(a﹣b)(a+b)(a2+b2)(a4﹣b4)=a8﹣b8.其中正确的是 (只需填写相应的序号).
12.已知(2x+m)(3x﹣2)=6x2﹣nx﹣4,则m+n的值为 .
13.设M=x+y,N=x﹣y,P=xy.若M=1,N=2,则P= .
14.已知(x2﹣x﹣1)x+2=1,则x= .
15.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则矩形的周长为 .
16.我们知道下面的结论:若am=an(a>0,且a≠1),则m=n.利用这个结论解决下列问题:设2m=3,2n=6,2p=12.现给出m,n,p三者之间的三个关系式:①m+p=2n,②m+n=2p﹣3,③n+p=4m.其中正确的是 .(填编号)
三.解答题(共7小题,共66分)
17.(10分)计算题:
(1)(﹣3a2b)2(2ab2)÷(﹣9a4b2).
(2)(2a+b)(b﹣2a)﹣(a﹣3b)2.
(3)(m﹣2n+3)(m+2n﹣3).
(4)20182﹣2017×2019(用乘法公式计算).
(5)化简求值:[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x,其中x=﹣2,y=1.
18.(8分)用简便方法计算.
(1)186.72﹣2×186.7×86.7+86.72;
(2)(3+1)(32+1)(34+1)(38+1).
19.(12分)先化简,再求值
(1)已知2x+y=1,求代数式(y+1)2﹣(y2﹣4x+4)的值.
(2)已知n为正整数,且x2n=4,求(x3n)2﹣2(x2)2n的值.
(3)若x、y满足,,求下列各式的值.
①(x+y)2;
②x4+y4.
20.(6分)定义一种新运算:观察下列各式:
1⊙3=1×4+3=7;3⊙(﹣1)=3×4﹣1=11;5⊙4=5×4+4=24;4⊙(﹣3)=4×4﹣3=13.
(1)请你想一想:a⊙b= ;
(2)若a≠b,那么a⊙b b⊙a(填“=”或“≠”);
(3)先化简,再求值:(a﹣b)⊙(2a+b),其中a=1,b=2.
21.(10分)如图,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是: (请选择正确的选项);
A.a2﹣ab=a(a﹣b) B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b) D.a2﹣b2=(a+b)(a﹣b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知9a2﹣b2=36,3a+b=9,则3a﹣b= ;
②计算:.
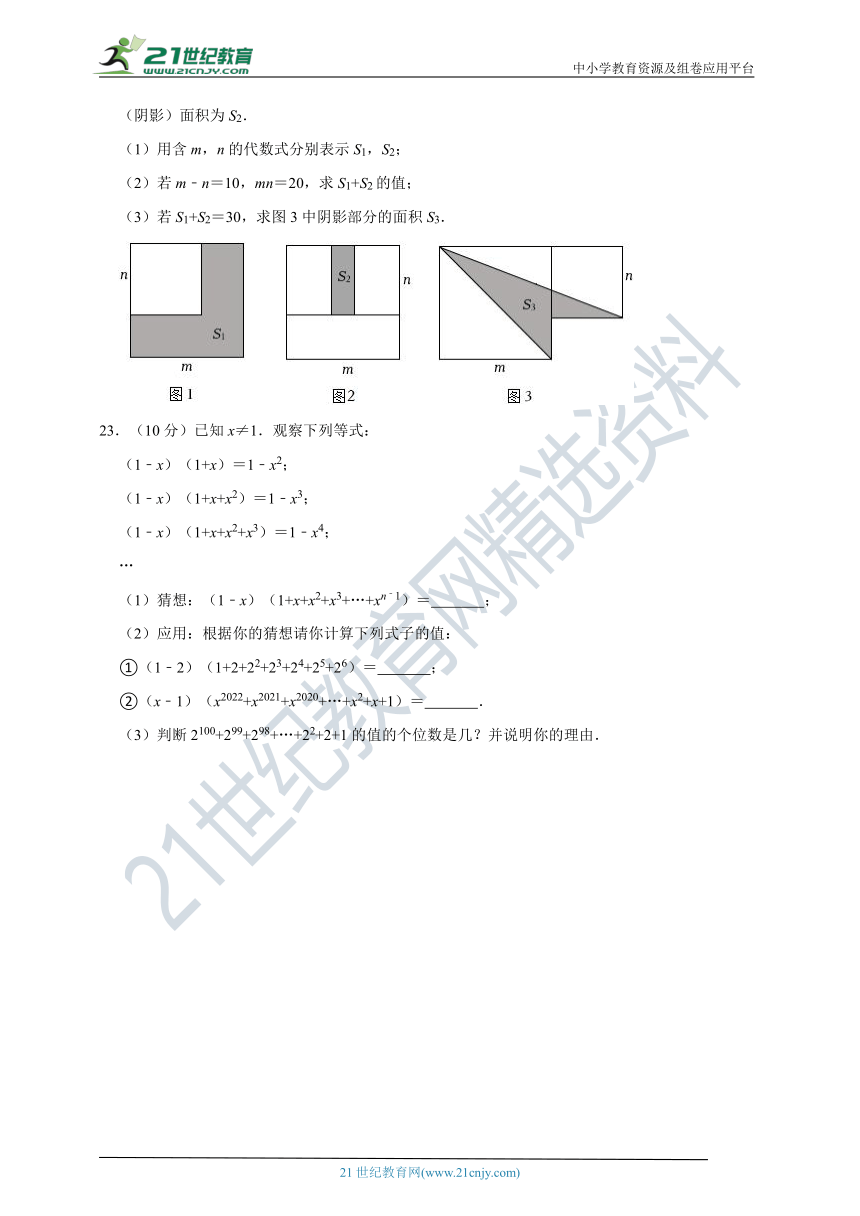
22.(10分)两个边长分别为m和n的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若在图1中大正方形的右上角再摆放一个边长为n的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含m,n的代数式分别表示S1,S2;
(2)若m﹣n=10,mn=20,求S1+S2的值;
(3)若S1+S2=30,求图3中阴影部分的面积S3.
23.(10分)已知x≠1.观察下列等式:
(1﹣x)(1+x)=1﹣x2;
(1﹣x)(1+x+x2)=1﹣x3;
(1﹣x)(1+x+x2+x3)=1﹣x4;
…
(1)猜想:(1﹣x)(1+x+x2+x3+…+xn﹣1)= ;
(2)应用:根据你的猜想请你计算下列式子的值:
①(1﹣2)(1+2+22+23+24+25+26)= ;
②(x﹣1)(x2022+x2021+x2020+…+x2+x+1)= .
(3)判断2100+299+298+…+22+2+1的值的个位数是几?并说明你的理由.
答案与解析
一.选择题
1.下列计算正确的有:①(﹣1)0=1;②;③(﹣x3)m=(﹣xm)3;④;⑤(a﹣3b)(﹣3b﹣a)=a2﹣9b2.( )
A.4个 B.3个 C.2个 D.1个
【点拨】各式计算得到结果,即可作出判断.
【解析】解:①(﹣1)0=1,正确;
②3×3﹣2=,正确;
③当m为奇数时有(﹣x3)m=(﹣xm)3=﹣x3m,错误;
④(x﹣)2=x2﹣x+,错误;
⑤(a﹣3b)(﹣3b﹣a)=﹣a2+9b2,错误,
故选:C.
【点睛】此题考查了平方差公式,幂的乘方与积的乘方,完全平方公式,零指数幂、负整数指数幂的规定,熟练掌握平方差公式及幂的运算法则是解本题的关键.
2.利用完全平方公式计算(﹣s2+t)2应等于( )
A.﹣s2﹣2st+t2 B.﹣s4﹣2s2t+t2 C.s4﹣2s2t+t2 D.s4﹣2st﹣t2
【点拨】根据完全平方公式计算即可.
【解析】解:(﹣s2+t)2=s4﹣2s2t+t2.
故选:C.
【点睛】本题考查了完全平方公式,掌握(a±b)2=a2±2ab+b2是解题的关键.
3.若(x+a)(x﹣5)=x2+bx﹣10,则ab﹣a+b的值是( )
A.﹣11 B.﹣7 C.﹣6 D.﹣55
【点拨】先利用多项式乘多项式法则计算等式的左边,根据等式得到a、b的值,代入计算出代数式ab﹣a+b的值.
【解析】解:∵(x+a)(x﹣5)=x2+(a﹣5)x﹣5a,
又∵(x+a)(x﹣5)=x2+bx﹣10,
∴x2+(a﹣5)x﹣5a=x2+bx﹣10.
∴a﹣5=b,﹣5a=﹣10.
∴a=2,b=﹣3.
∴ab﹣a+b=2×(﹣3)﹣2﹣3=﹣11.
故选:A.
【点睛】本题考查了多项式乘多项式,掌握多项式乘多项式法则是解决本题的关键.
4.已知(x+y)2=49,(x﹣y)2=25,则xy=( )
A.﹣6 B.6 C.12 D.24
【点拨】先把所求式子变形为完全平方式,再把题中已知条件代入即可解答.
【解析】解:因为(x+y)2﹣(x﹣y)2=4xy=49﹣25=24,
所以xy=6,
故选:B.
【点睛】本题考查了完全平方公式,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式,完全平方公式:(a±b)2=a2±2ab+b2.
5.已知关于x的多项式ax﹣b与3x2+x+2的乘积展开式中不含x的二次项,且一次项系数为﹣5,则ab的值为( )
A.﹣ B. C.﹣3 D.3
【点拨】利用多项式乘多项式的法则进行运算,再结合条件进行求解即可.
【解析】解:(ax﹣b)(3x2+x+2)
=3ax3+ax2+2ax﹣3bx2﹣bx﹣2b
=3ax3+(a﹣3b)x2+(2a﹣b)x﹣2b,
∵展开式中不含x的二次项,且一次项系数为﹣5,
∴a﹣3b=0,2a﹣b=﹣5,
解得:a=﹣3,b=﹣1,
∴ab=.
故选:A.
【点睛】本题主要考查多项式乘多项式,解答的关键是对相应的运算法则的掌握.
6.如图,4张长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2.若S1=2S2,则a、b满足( )
A.a=3b B.a=2b C.2a=5b D.2a=3b
【点拨】先用a、b的代数式分别表示S1=a2+2b2,S2=2ab﹣b2,再根据S1=2S2,得a2+2b2=2(2ab﹣b2),整理,得(a﹣2b)2=0,所以a=2b.
【解析】解:S1=b(a+b)×2+ab×2+(a﹣b)2=a2+2b2,
S2=(a+b)2﹣S1=(a+b)2﹣(a2+2b2)=2ab﹣b2,
∵S1=2S2,
∴a2+2b2=2(2ab﹣b2),
整理,得(a﹣2b)2=0,
∴a﹣2b=0,
∴a=2b.
故选:B.
【点睛】本题考查了整式的混合运算,熟练运用完全平方公式是解题的关键.
7.2×(3+1)(32+1)(34+1)(38+1)(316+1)+1的计算结果是( )
A.332+1 B.332﹣1 C.331 D.332
【点拨】把因数2写成3﹣1后,利用平方差公式依次计算即可得出结果.
【解析】解:2×(3+1)(32+1)(34+1)(38+1)(316+1)+1
=(3﹣1)(3+1)(32+1)(34+1)(38+1)(316+1)+1
=(32﹣1)(32+1)(34+1)(38+1)(316+1)+1
=(34﹣1)(34+1)(38+1)(316+1)+1
=(38﹣1)(38+1)(316+1)+1
=(316﹣1)(316+1)+1
=332﹣1+1
=332,
故选:D.
【点睛】本题考查了平方差公式,把因数2写成3﹣1是利用平方差公式的关键.
8.若4x2+1加上一个单项式后能成为一个多项式的完全平方式,则这个单项式可能就是下列单项式:①﹣1;②﹣4x2;③4x4;④4x;⑤﹣4x中的( )
A.①②③④⑤ B.③④⑤ C.①②④⑤ D.②③④⑤
【点拨】根据完全平方公式的结构特征逐个进行判断即可.
【解析】解:4x2+1﹣1=4x2是单项式,因此①不合适;
4x2+1﹣4x2=1是单项式,因此②不合适;
4x2+1+4x4=(2x2+1)2,因此③合适;
4x2+1+4x=(2x+1)2,因此④合适;
4x2+1﹣4x=(2x﹣1)2,因此⑤合适;
故选:B.
【点睛】本题考查完全平方公式,掌握完全平方公式的结构特征是正确判断的关键.
9.已知(x﹣2020)2+(x﹣2022)2=18,则(x﹣2021)2的值是( )
A.4 B.8 C.12 D.16
【点拨】先变形为[(x﹣2021)+1]2+[(x﹣2021)﹣1]2=18,然后利用完全平方公式展开即可得到(x﹣2021)2的值.
【解析】解:∵(x﹣2020)2+(x﹣2022)2=18,
∴[(x﹣2021)+1]2+[(x﹣2021)﹣1]2=18,
∴(x﹣2021)2+2(x﹣2021)+1+(x﹣2021)2﹣2(x﹣2021)+1=18,
∴(x﹣2021)2=8.
故选:B.
【点睛】本题考查了完全平方公式:(a±b)2=a2±2ab+b2.
10.如图,方形网格能验证下列哪个选项中的等式成立( )
A.(a+b+c)2=a2+b2+c2 B.(a+b+c)2=a2+b2+c2+2abc
C.(a+b+c)2=a2+b2+c2+ab+bc+ac D.(a+b+c)2=a2+b2+c2+2ab+2bc+2ac
【点拨】根据正方形和矩形的面积公式即可得到结论.
【解析】解:∵图形的面积=(a+b+c)2,图形的面积=a2+2ab+2ac+b2+c2+2bc,
∴(a+b+c)2=a2+2ab+2ac+b2+c2+2bc,
故选:D.
【点睛】本题考查了完全平方公式的几何背景,熟练掌握正方形和矩形的面积公式是解题的关键.
二.填空题
11.现有以下几个算式:
(1)(0.5﹣)0=1;(2)﹣x (﹣x)6=x7;(3)(﹣a2)3=a6;(4)(b﹣a)2=b2﹣ab+a2;(5)(﹣a﹣2b)(a﹣2b)=﹣a2+4b2;(6)(a﹣b)(a+b)(a2+b2)(a4﹣b4)=a8﹣b8.其中正确的是 (4)(5)(6) (只需填写相应的序号).
【点拨】根据零指数幂判断(1);根据同底数幂的乘法判断(2);根据幂的乘方和积的乘方判断(3);根据完全平方公式判断(4);根据平方差公式判断(5);根据平方差公式的连用判断(6).
【解析】解:∵0.5﹣=0,
∴(0.5﹣)0没有意义,故(1)不符合题意;
﹣x (﹣x)6=(﹣x)7=﹣x7,故(2)不符合题意;
(﹣a2)3=﹣a6,故(3)不符合题意;
(b﹣a)2=b2﹣ab+a2,故(4)符合题意;
(﹣a﹣2b)(a﹣2b)=4b2﹣a2=﹣a2+4b2,故(5)符合题意;
(a﹣b)(a+b)(a2+b2)(a4﹣b4)
=(a2﹣b2)(a2+b2)(a4﹣b4)
=(a4﹣b4)(a4﹣b4)
=a8﹣b8,故(6)符合题意;
故答案为:(4)(5)(6).
【点睛】本题考查了零指数幂,同底数幂的乘法,幂的乘方和积的乘方,完全平方公式,平方差公式,掌握(a+b)(a﹣b)=a2﹣b2,(a±b)2=a2±2ab+b2是解题的关键.
12.已知(2x+m)(3x﹣2)=6x2﹣nx﹣4,则m+n的值为 0 .
【点拨】利用多项式乘多项式的法则将等式左边进行计算,对比等式右边得出关于m,n的等式,求出m,n的值,代入计算即可得出答案.
【解析】解:∵(2x+m)(3x﹣2)=6x2﹣nx﹣4,
∴6x2﹣4x+3mx﹣2m=6x2﹣nx﹣4,
∴6x2+(3m﹣4)x﹣2m=6x2﹣nx﹣4,
∴3m﹣4=﹣n,﹣2m=﹣4,
∴m=2,n=﹣2,
∴m+n=2﹣2=0,
故答案为:0.
【点睛】本题考查了多项式乘多项式,掌握多项式乘多项式的法则是解决问题的关键.
13.设M=x+y,N=x﹣y,P=xy.若M=1,N=2,则P= ﹣ .
【点拨】根据完全平方公式得到(x+y)2=x2+2xy+y2=1,(x﹣y)2=x2﹣2xy+y2=4,两式相减即可求解.
【解析】解:法一:(x+y)2=x2+2xy+y2=1,(x﹣y)2=x2﹣2xy+y2=4,
两式相减得4xy=﹣3,
解得xy=﹣,
则P=﹣.
法二:由题可得,
解之得:,
∴P=xy=﹣,
故答案为:﹣.
【点睛】本题考查了完全平方公式,完全平方公式:(a±b)2=a2±2ab+b2.
14.已知(x2﹣x﹣1)x+2=1,则x= ﹣2或﹣1或0或2 .
【点拨】要使结果为1,可分为三种情况:①当指数是0时,②当底数为1时,③当底数为(﹣1)时,分别求出x即可得出答案.
【解析】解:①当x+2=0,即x=﹣2时,x2﹣x﹣1≠0,
∴x=﹣2,成立;
②当x2﹣x﹣1=1时,
解得:x=2或﹣1,
∴x=2或﹣1,成立;
③当x2﹣x﹣1=﹣1时,
解得:x=0或1,
当x=0时,(﹣1)2=1,成立,
当x=1时,(﹣1)3=﹣1,不成立,
故答案为:﹣2或﹣1或0或2.
【点睛】本题考查了零指数幂和有理数的乘方,掌握零指数幂的意义,有理数乘方的意义是解决问题的关键.
15.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则矩形的周长为 (4a+16)cm .
【点拨】根据图形可得所拼矩形的长为[(a+4)+(a+1)]cm,宽为[(a+4)﹣(a+1)]cm,从而可计算出此题结果.
【解析】解:由题意得,所拼矩形的周长为:
2[(a+4)+(a+1)+(a+4)﹣(a+1)]
=2(2a+5+3)
=2(2a+8)
=(4a+16)cm,
故答案为:(4a+16)cm.
【点睛】此题考查了整式运算几何背景问题的解决能力,关键是能根据图形准确列式并计算.
16.我们知道下面的结论:若am=an(a>0,且a≠1),则m=n.利用这个结论解决下列问题:设2m=3,2n=6,2p=12.现给出m,n,p三者之间的三个关系式:①m+p=2n,②m+n=2p﹣3,③n+p=4m.其中正确的是 ①② .(填编号)
【点拨】由2n=6=2×3=2×2m=2m+1,得出n=m+1,由2p=12=22×3=22×2m=2m+2,得出p=m+2,进而得出p=n+1,进一步对m+p,m+n,n+p代入计算,即可得出答案.
【解析】解:∵2n=6=2×3=2×2m=2m+1,
∴n=m+1,
∵2p=12=22×3=22×2m=2m+2,
∴p=m+2,
∴p=n+1,
∴m+p=m+n+1=n+n=2n,
∴①符合题意;
∵m+n=p﹣2+p﹣1=2p﹣3,
∴②符合题意;
∵n+p=m+1+m+2=2m+3≠4m,
∴③不符合题意,
故答案为:①②.
【点睛】本题考查了幂的乘方与积的乘方,掌握幂的乘方与积的乘方的法则,同底数幂的乘法法则是解决问题的关键.
三.解答题
17.计算题:
(1)(﹣3a2b)2(2ab2)÷(﹣9a4b2).
(2)(2a+b)(b﹣2a)﹣(a﹣3b)2.
(3)(m﹣2n+3)(m+2n﹣3).
(4)20182﹣2017×2019(用乘法公式计算).
(5)化简求值:[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x,其中x=﹣2,y=1.
【点拨】(1)先算乘方,再算乘法,即可解答;
(2)利用平方差公式,完全平方公式进行计算即可解答;
(3)利用平方差公式,完全平方公式进行计算即可解答;
(4)利用平方差公式,进行计算即可解答;
(5)先去小括号,再去中括号,然后合并同类项,最后把x,y的值代入化简后的式子进行计算即可解答.
【解析】解:(1)(﹣3a2b)2(2ab2)÷(﹣9a4b2)
=9a4b2 2ab2÷(﹣9a4b2)
=18a5b4÷(﹣9a4b2)
=﹣2ab2;
(2)(2a+b)(b﹣2a)﹣(a﹣3b)2
=b2﹣4a2﹣a2+6ab﹣9b2
=﹣8b2﹣5a2+6ab;
(3)(m﹣2n+3)(m+2n﹣3)
=[m﹣(2n﹣3)][m+(2n﹣3)]
=m2﹣(2n﹣3)2
=m2﹣4n2+12n﹣9;
(4)20182﹣2017×2019
=20182﹣(2018﹣1)(2018+1)
=20182﹣20182+1
=1;
(5)[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x
=(x2+4xy+4y2﹣3x2﹣2xy+y2﹣5y2)÷2x
=(﹣2x2+2xy)÷2x
=﹣x+y,
当x=﹣2,y=1时,原式=﹣(﹣2)+1=3.
【点睛】本题考查了整式的混合运算﹣化简求值,准确熟练地进行计算是解题的关键.
18.用简便方法计算.
(1)186.72﹣2×186.7×86.7+86.72;
(2)(3+1)(32+1)(34+1)(38+1).
【点拨】(1)根据完全平方公式将原式化为(186.7﹣86.7)2即可;
(2)配上因式(3﹣1),连续使用平方差公式进行计算即可.
【解析】解:(1)原式=(186.7﹣86.7)2=1002=10000;
(2)原式=(3﹣1)(3+1)(32+1)(34+1)(38+1)
=(32﹣1)(32+1)(34+1)(38+1)
=(34﹣1)(34+1)(38+1)
=(38﹣1)(38+1)
=(316﹣1)
=.
【点睛】本题考查平方差公式、完全平方公式,掌握完全平方公式、平方差公式的结构特征是正确解答的前提.
19.先化简,再求值
(1)已知2x+y=1,求代数式(y+1)2﹣(y2﹣4x+4)的值.
(2)已知n为正整数,且x2n=4,求(x3n)2﹣2(x2)2n的值.
(3)若x、y满足,,求下列各式的值.
①(x+y)2;
②x4+y4.
【点拨】(1)根据完全平方公式化简后,再把2x+y=1代入计算即可;
(2)根据幂的乘方的运算法则化简后,把x2n=4代入计算即可;
(3)根据完全平方公式求解即可.
【解析】解:(1)∵2x+y=1,
∴(y+1)2﹣(y2﹣4x+4)
=y2+2y+1﹣y2+4x﹣4
=4x+2y﹣3
=2(2x+y)﹣3
=2﹣3
=﹣1;
(2)∵x2n=4,
∴(x3n)2﹣2(x2)2n=(x2n)3﹣2(22n)2=43﹣2×42=64﹣2×16=32;
(3)①∵,,
∴(x+y)2=x2+y2+2xy===;
②∵,,
∴x4+y4=(x2+y2)2﹣2x2y2===.
【点睛】本题主要考查了整式的混合运算,幂的乘方以及完全平方公式,熟记相关公式与运算法则是解答本题的关键.
20.定义一种新运算:观察下列各式:
1⊙3=1×4+3=7;3⊙(﹣1)=3×4﹣1=11;5⊙4=5×4+4=24;4⊙(﹣3)=4×4﹣3=13.
(1)请你想一想:a⊙b= 4a+b ;
(2)若a≠b,那么a⊙b ≠ b⊙a(填“=”或“≠”);
(3)先化简,再求值:(a﹣b)⊙(2a+b),其中a=1,b=2.
【点拨】(1)根据题目中的新运算,可以求出结果;
(2)根据(1)的结果和b⊙a结果比较;
(3)根据新运算将式子化简,然后代入a,b的值即可求出所得之值.
【解析】解:(1)a⊙b=4a+b.
故答案为:4a+b.
(2)a⊙b=4a+b,b⊙a=4b+a,
∵a≠b,
∴a⊙b≠b⊙a.
故答案为:≠
(3)(a﹣b)⊙(2a+b)
=4(a﹣b)+(2a+b)
=4a﹣4b+2a+b
=6a﹣3b.
当a=1,b=2时,原式=6×1﹣3×2=0.
【点睛】考查整式的化简求值,解决本题的关键是明确整式混合运算的计算方法.
21.如图,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是: D (请选择正确的选项);
A.a2﹣ab=a(a﹣b) B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b) D.a2﹣b2=(a+b)(a﹣b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知9a2﹣b2=36,3a+b=9,则3a﹣b= 4 ;
②计算:.
【点拨】(1)图1阴影部分的面积可以看作两个正方形的面积差,即a2﹣b2,图2阴影部分是长为a+b,宽为a﹣b的长方形,可表示其面积,由两种方法所求的面积相等可得答案;
(2)①根据平方差公式将9a2﹣b2=36转化为(3a+b)(3a﹣b)=36,再根据3a+b=9,进而求出3a﹣b的值;
②利用平方差公式将原式化为(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+),进而得出××××××××…××即可.
【解析】解:(1)图1阴影部分的面积可以看作两个正方形的面积差,即a2﹣b2,
图2阴影部分是长为a+b,宽为a﹣b的长方形,因此面积为(a+b)(a﹣b),
由图1、图2的面积相等得,a2﹣b2=(a+b)(a﹣b),
故答案为:D;
(2)①∵9a2﹣b2=36,
∴(3a+b)(3a﹣b)=36,
又∵3a+b=9,
∴3a﹣b=36÷9=4,
故答案为:4;
②原式=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)
=××××××××…××
=×
=.
【点睛】本题考查完全平方公式的几何背景,掌握完全平方公式的结构特征是正确解答的前提.
22.两个边长分别为m和n的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若在图1中大正方形的右上角再摆放一个边长为n的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含m,n的代数式分别表示S1,S2;
(2)若m﹣n=10,mn=20,求S1+S2的值;
(3)若S1+S2=30,求图3中阴影部分的面积S3.
【点拨】(1)S1可以看作两个正方形的面积差,即S1=m2﹣n2,S2是长为2n﹣m,高为n的长方形的面积,即S2=(2n﹣m) n=2n2﹣mn;
(2)将S1+S2=m2﹣n2+2n2﹣mn,变形为(m﹣n)2+mn,再代入计算即可;
(3)由S1+S2=30,可得到m2+n2﹣mn=30,由图3看得出S3=(m2+n2﹣mn),整体代入计算即可.
【解析】解:(1)S1可以看作两个正方形的面积差,即S1=m2﹣n2,
S2是长为2n﹣m,高为n的长方形的面积,即S2=(2n﹣m) n=2n2﹣mn;
(2)∵m﹣n=10,mn=20,
∴S1+S2=m2﹣n2+2n2﹣mn
=m2+n2﹣mn
=(m﹣n)2+mn
=100+20
=120;
(3)∵S1+S2=m2+n2﹣mn=30,
∴S3=m2+n2﹣m2﹣n(m+n)
=m2﹣mn+n2
=(m2+n2﹣mn)
=×30
=15.
【点睛】本题考查完全平方公式的几何背景,掌握完全平方公式的结构特征是正确解答的前提.
23.已知x≠1.观察下列等式:
(1﹣x)(1+x)=1﹣x2;
(1﹣x)(1+x+x2)=1﹣x3;
(1﹣x)(1+x+x2+x3)=1﹣x4;
…
(1)猜想:(1﹣x)(1+x+x2+x3+…+xn﹣1)= 1﹣xn ;
(2)应用:根据你的猜想请你计算下列式子的值:
①(1﹣2)(1+2+22+23+24+25+26)= ﹣127 ;
②(x﹣1)(x2022+x2021+x2020+…+x2+x+1)= x2023﹣1 .
(3)判断2100+299+298+…+22+2+1的值的个位数是几?并说明你的理由.
【点拨】(1)根据所给的等式,不难得出结果;
(2)①利用(1)中的结论进行求解即可;
②利用(1)中的结论进行求解即可;
(3)先利用(1)的结论进行求解,再判断其个位数即可.
【解析】解:(1)∵(1﹣x)(1+x)=1﹣x2;
(1﹣x)(1+x+x2)=1﹣x3;
(1﹣x)(1+x+x2+x3)=1﹣x4
…
∴(1﹣x)(1+x+x2+x3+…+xn﹣1)=1﹣xn;
故答案为:1﹣xn;
(2)①(1﹣2)(1+2+22+23+24+25+26)
=1﹣27
=1﹣128
=﹣127;
故答案为:﹣127;
(2)②(x﹣1)(x2022+x2021+x2020+…+x2+x+1)
=﹣(1﹣x)(1+x+x2+…+x2022)
=﹣(1﹣x2023)
=x2023﹣1.
故答案为:x2023﹣1;
(3)1,理由如下:
2100+299+298+…+22+2+1
=﹣(1﹣2)×(1+2+22+…+2100)
=﹣(1﹣2101)
=2101﹣1.
∵21的个位数是2,
22的个位数是4,
23的个位数是8,
24的个位数是6,
25的个位数是2,
…
∴其个位数以2,4,8,6不断循环出现,
∵101÷4=25……1,
∴2101的个位数字是2,
∴2101﹣1的个位数是1.
【点睛】本题主要考查多项式乘多项式,数字的变化规律,解答的关键是对相应的运算法则的掌握.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
2022-2023学年浙教版七年级下第3章 整式的乘除 单元检测卷(2)
一.选择题(共10小题,每小题3分,共30分)
1.下列计算正确的有:①(﹣1)0=1;②;③(﹣x3)m=(﹣xm)3;④;⑤(a﹣3b)(﹣3b﹣a)=a2﹣9b2.( )
A.4个 B.3个 C.2个 D.1个
2.利用完全平方公式计算(﹣s2+t)2应等于( )
A.﹣s2﹣2st+t2 B.﹣s4﹣2s2t+t2 C.s4﹣2s2t+t2 D.s4﹣2st﹣t2
3.若(x+a)(x﹣5)=x2+bx﹣10,则ab﹣a+b的值是( )
A.﹣11 B.﹣7 C.﹣6 D.﹣55
4.已知(x+y)2=49,(x﹣y)2=25,则xy=( )
A.﹣6 B.6 C.12 D.24
5.已知关于x的多项式ax﹣b与3x2+x+2的乘积展开式中不含x的二次项,且一次项系数为﹣5,则ab的值为( )
A.﹣ B. C.﹣3 D.3
6.如图,4张长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2.若S1=2S2,则a、b满足( )
A.a=3b B.a=2b C.2a=5b D.2a=3b
7.2×(3+1)(32+1)(34+1)(38+1)(316+1)+1的计算结果是( )
A.332+1 B.332﹣1 C.331 D.332
8.若4x2+1加上一个单项式后能成为一个多项式的完全平方式,则这个单项式可能就是下列单项式:①﹣1;②﹣4x2;③4x4;④4x;⑤﹣4x中的( )
A.①②③④⑤ B.③④⑤ C.①②④⑤ D.②③④⑤
9.已知(x﹣2020)2+(x﹣2022)2=18,则(x﹣2021)2的值是( )
A.4 B.8 C.12 D.16
10.如图,方形网格能验证下列哪个选项中的等式成立( )
A.(a+b+c)2=a2+b2+c2 B.(a+b+c)2=a2+b2+c2+2abc
C.(a+b+c)2=a2+b2+c2+ab+bc+ac D.(a+b+c)2=a2+b2+c2+2ab+2bc+2ac
二.填空题(共6小题,每小题4分,共24分)
11.现有以下几个算式:
(1)(0.5﹣)0=1;(2)﹣x (﹣x)6=x7;(3)(﹣a2)3=a6;(4)(b﹣a)2=b2﹣ab+a2;(5)(﹣a﹣2b)(a﹣2b)=﹣a2+4b2;(6)(a﹣b)(a+b)(a2+b2)(a4﹣b4)=a8﹣b8.其中正确的是 (只需填写相应的序号).
12.已知(2x+m)(3x﹣2)=6x2﹣nx﹣4,则m+n的值为 .
13.设M=x+y,N=x﹣y,P=xy.若M=1,N=2,则P= .
14.已知(x2﹣x﹣1)x+2=1,则x= .
15.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则矩形的周长为 .
16.我们知道下面的结论:若am=an(a>0,且a≠1),则m=n.利用这个结论解决下列问题:设2m=3,2n=6,2p=12.现给出m,n,p三者之间的三个关系式:①m+p=2n,②m+n=2p﹣3,③n+p=4m.其中正确的是 .(填编号)
三.解答题(共7小题,共66分)
17.(10分)计算题:
(1)(﹣3a2b)2(2ab2)÷(﹣9a4b2).
(2)(2a+b)(b﹣2a)﹣(a﹣3b)2.
(3)(m﹣2n+3)(m+2n﹣3).
(4)20182﹣2017×2019(用乘法公式计算).
(5)化简求值:[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x,其中x=﹣2,y=1.
18.(8分)用简便方法计算.
(1)186.72﹣2×186.7×86.7+86.72;
(2)(3+1)(32+1)(34+1)(38+1).
19.(12分)先化简,再求值
(1)已知2x+y=1,求代数式(y+1)2﹣(y2﹣4x+4)的值.
(2)已知n为正整数,且x2n=4,求(x3n)2﹣2(x2)2n的值.
(3)若x、y满足,,求下列各式的值.
①(x+y)2;
②x4+y4.
20.(6分)定义一种新运算:观察下列各式:
1⊙3=1×4+3=7;3⊙(﹣1)=3×4﹣1=11;5⊙4=5×4+4=24;4⊙(﹣3)=4×4﹣3=13.
(1)请你想一想:a⊙b= ;
(2)若a≠b,那么a⊙b b⊙a(填“=”或“≠”);
(3)先化简,再求值:(a﹣b)⊙(2a+b),其中a=1,b=2.
21.(10分)如图,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是: (请选择正确的选项);
A.a2﹣ab=a(a﹣b) B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b) D.a2﹣b2=(a+b)(a﹣b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知9a2﹣b2=36,3a+b=9,则3a﹣b= ;
②计算:.
22.(10分)两个边长分别为m和n的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若在图1中大正方形的右上角再摆放一个边长为n的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含m,n的代数式分别表示S1,S2;
(2)若m﹣n=10,mn=20,求S1+S2的值;
(3)若S1+S2=30,求图3中阴影部分的面积S3.
23.(10分)已知x≠1.观察下列等式:
(1﹣x)(1+x)=1﹣x2;
(1﹣x)(1+x+x2)=1﹣x3;
(1﹣x)(1+x+x2+x3)=1﹣x4;
…
(1)猜想:(1﹣x)(1+x+x2+x3+…+xn﹣1)= ;
(2)应用:根据你的猜想请你计算下列式子的值:
①(1﹣2)(1+2+22+23+24+25+26)= ;
②(x﹣1)(x2022+x2021+x2020+…+x2+x+1)= .
(3)判断2100+299+298+…+22+2+1的值的个位数是几?并说明你的理由.
答案与解析
一.选择题
1.下列计算正确的有:①(﹣1)0=1;②;③(﹣x3)m=(﹣xm)3;④;⑤(a﹣3b)(﹣3b﹣a)=a2﹣9b2.( )
A.4个 B.3个 C.2个 D.1个
【点拨】各式计算得到结果,即可作出判断.
【解析】解:①(﹣1)0=1,正确;
②3×3﹣2=,正确;
③当m为奇数时有(﹣x3)m=(﹣xm)3=﹣x3m,错误;
④(x﹣)2=x2﹣x+,错误;
⑤(a﹣3b)(﹣3b﹣a)=﹣a2+9b2,错误,
故选:C.
【点睛】此题考查了平方差公式,幂的乘方与积的乘方,完全平方公式,零指数幂、负整数指数幂的规定,熟练掌握平方差公式及幂的运算法则是解本题的关键.
2.利用完全平方公式计算(﹣s2+t)2应等于( )
A.﹣s2﹣2st+t2 B.﹣s4﹣2s2t+t2 C.s4﹣2s2t+t2 D.s4﹣2st﹣t2
【点拨】根据完全平方公式计算即可.
【解析】解:(﹣s2+t)2=s4﹣2s2t+t2.
故选:C.
【点睛】本题考查了完全平方公式,掌握(a±b)2=a2±2ab+b2是解题的关键.
3.若(x+a)(x﹣5)=x2+bx﹣10,则ab﹣a+b的值是( )
A.﹣11 B.﹣7 C.﹣6 D.﹣55
【点拨】先利用多项式乘多项式法则计算等式的左边,根据等式得到a、b的值,代入计算出代数式ab﹣a+b的值.
【解析】解:∵(x+a)(x﹣5)=x2+(a﹣5)x﹣5a,
又∵(x+a)(x﹣5)=x2+bx﹣10,
∴x2+(a﹣5)x﹣5a=x2+bx﹣10.
∴a﹣5=b,﹣5a=﹣10.
∴a=2,b=﹣3.
∴ab﹣a+b=2×(﹣3)﹣2﹣3=﹣11.
故选:A.
【点睛】本题考查了多项式乘多项式,掌握多项式乘多项式法则是解决本题的关键.
4.已知(x+y)2=49,(x﹣y)2=25,则xy=( )
A.﹣6 B.6 C.12 D.24
【点拨】先把所求式子变形为完全平方式,再把题中已知条件代入即可解答.
【解析】解:因为(x+y)2﹣(x﹣y)2=4xy=49﹣25=24,
所以xy=6,
故选:B.
【点睛】本题考查了完全平方公式,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式,完全平方公式:(a±b)2=a2±2ab+b2.
5.已知关于x的多项式ax﹣b与3x2+x+2的乘积展开式中不含x的二次项,且一次项系数为﹣5,则ab的值为( )
A.﹣ B. C.﹣3 D.3
【点拨】利用多项式乘多项式的法则进行运算,再结合条件进行求解即可.
【解析】解:(ax﹣b)(3x2+x+2)
=3ax3+ax2+2ax﹣3bx2﹣bx﹣2b
=3ax3+(a﹣3b)x2+(2a﹣b)x﹣2b,
∵展开式中不含x的二次项,且一次项系数为﹣5,
∴a﹣3b=0,2a﹣b=﹣5,
解得:a=﹣3,b=﹣1,
∴ab=.
故选:A.
【点睛】本题主要考查多项式乘多项式,解答的关键是对相应的运算法则的掌握.
6.如图,4张长为a,宽为b(a>b)的长方形纸片,按如图的方式拼成一个边长为(a+b)的正方形,图中空白部分的面积为S1,阴影部分的面积为S2.若S1=2S2,则a、b满足( )
A.a=3b B.a=2b C.2a=5b D.2a=3b
【点拨】先用a、b的代数式分别表示S1=a2+2b2,S2=2ab﹣b2,再根据S1=2S2,得a2+2b2=2(2ab﹣b2),整理,得(a﹣2b)2=0,所以a=2b.
【解析】解:S1=b(a+b)×2+ab×2+(a﹣b)2=a2+2b2,
S2=(a+b)2﹣S1=(a+b)2﹣(a2+2b2)=2ab﹣b2,
∵S1=2S2,
∴a2+2b2=2(2ab﹣b2),
整理,得(a﹣2b)2=0,
∴a﹣2b=0,
∴a=2b.
故选:B.
【点睛】本题考查了整式的混合运算,熟练运用完全平方公式是解题的关键.
7.2×(3+1)(32+1)(34+1)(38+1)(316+1)+1的计算结果是( )
A.332+1 B.332﹣1 C.331 D.332
【点拨】把因数2写成3﹣1后,利用平方差公式依次计算即可得出结果.
【解析】解:2×(3+1)(32+1)(34+1)(38+1)(316+1)+1
=(3﹣1)(3+1)(32+1)(34+1)(38+1)(316+1)+1
=(32﹣1)(32+1)(34+1)(38+1)(316+1)+1
=(34﹣1)(34+1)(38+1)(316+1)+1
=(38﹣1)(38+1)(316+1)+1
=(316﹣1)(316+1)+1
=332﹣1+1
=332,
故选:D.
【点睛】本题考查了平方差公式,把因数2写成3﹣1是利用平方差公式的关键.
8.若4x2+1加上一个单项式后能成为一个多项式的完全平方式,则这个单项式可能就是下列单项式:①﹣1;②﹣4x2;③4x4;④4x;⑤﹣4x中的( )
A.①②③④⑤ B.③④⑤ C.①②④⑤ D.②③④⑤
【点拨】根据完全平方公式的结构特征逐个进行判断即可.
【解析】解:4x2+1﹣1=4x2是单项式,因此①不合适;
4x2+1﹣4x2=1是单项式,因此②不合适;
4x2+1+4x4=(2x2+1)2,因此③合适;
4x2+1+4x=(2x+1)2,因此④合适;
4x2+1﹣4x=(2x﹣1)2,因此⑤合适;
故选:B.
【点睛】本题考查完全平方公式,掌握完全平方公式的结构特征是正确判断的关键.
9.已知(x﹣2020)2+(x﹣2022)2=18,则(x﹣2021)2的值是( )
A.4 B.8 C.12 D.16
【点拨】先变形为[(x﹣2021)+1]2+[(x﹣2021)﹣1]2=18,然后利用完全平方公式展开即可得到(x﹣2021)2的值.
【解析】解:∵(x﹣2020)2+(x﹣2022)2=18,
∴[(x﹣2021)+1]2+[(x﹣2021)﹣1]2=18,
∴(x﹣2021)2+2(x﹣2021)+1+(x﹣2021)2﹣2(x﹣2021)+1=18,
∴(x﹣2021)2=8.
故选:B.
【点睛】本题考查了完全平方公式:(a±b)2=a2±2ab+b2.
10.如图,方形网格能验证下列哪个选项中的等式成立( )
A.(a+b+c)2=a2+b2+c2 B.(a+b+c)2=a2+b2+c2+2abc
C.(a+b+c)2=a2+b2+c2+ab+bc+ac D.(a+b+c)2=a2+b2+c2+2ab+2bc+2ac
【点拨】根据正方形和矩形的面积公式即可得到结论.
【解析】解:∵图形的面积=(a+b+c)2,图形的面积=a2+2ab+2ac+b2+c2+2bc,
∴(a+b+c)2=a2+2ab+2ac+b2+c2+2bc,
故选:D.
【点睛】本题考查了完全平方公式的几何背景,熟练掌握正方形和矩形的面积公式是解题的关键.
二.填空题
11.现有以下几个算式:
(1)(0.5﹣)0=1;(2)﹣x (﹣x)6=x7;(3)(﹣a2)3=a6;(4)(b﹣a)2=b2﹣ab+a2;(5)(﹣a﹣2b)(a﹣2b)=﹣a2+4b2;(6)(a﹣b)(a+b)(a2+b2)(a4﹣b4)=a8﹣b8.其中正确的是 (4)(5)(6) (只需填写相应的序号).
【点拨】根据零指数幂判断(1);根据同底数幂的乘法判断(2);根据幂的乘方和积的乘方判断(3);根据完全平方公式判断(4);根据平方差公式判断(5);根据平方差公式的连用判断(6).
【解析】解:∵0.5﹣=0,
∴(0.5﹣)0没有意义,故(1)不符合题意;
﹣x (﹣x)6=(﹣x)7=﹣x7,故(2)不符合题意;
(﹣a2)3=﹣a6,故(3)不符合题意;
(b﹣a)2=b2﹣ab+a2,故(4)符合题意;
(﹣a﹣2b)(a﹣2b)=4b2﹣a2=﹣a2+4b2,故(5)符合题意;
(a﹣b)(a+b)(a2+b2)(a4﹣b4)
=(a2﹣b2)(a2+b2)(a4﹣b4)
=(a4﹣b4)(a4﹣b4)
=a8﹣b8,故(6)符合题意;
故答案为:(4)(5)(6).
【点睛】本题考查了零指数幂,同底数幂的乘法,幂的乘方和积的乘方,完全平方公式,平方差公式,掌握(a+b)(a﹣b)=a2﹣b2,(a±b)2=a2±2ab+b2是解题的关键.
12.已知(2x+m)(3x﹣2)=6x2﹣nx﹣4,则m+n的值为 0 .
【点拨】利用多项式乘多项式的法则将等式左边进行计算,对比等式右边得出关于m,n的等式,求出m,n的值,代入计算即可得出答案.
【解析】解:∵(2x+m)(3x﹣2)=6x2﹣nx﹣4,
∴6x2﹣4x+3mx﹣2m=6x2﹣nx﹣4,
∴6x2+(3m﹣4)x﹣2m=6x2﹣nx﹣4,
∴3m﹣4=﹣n,﹣2m=﹣4,
∴m=2,n=﹣2,
∴m+n=2﹣2=0,
故答案为:0.
【点睛】本题考查了多项式乘多项式,掌握多项式乘多项式的法则是解决问题的关键.
13.设M=x+y,N=x﹣y,P=xy.若M=1,N=2,则P= ﹣ .
【点拨】根据完全平方公式得到(x+y)2=x2+2xy+y2=1,(x﹣y)2=x2﹣2xy+y2=4,两式相减即可求解.
【解析】解:法一:(x+y)2=x2+2xy+y2=1,(x﹣y)2=x2﹣2xy+y2=4,
两式相减得4xy=﹣3,
解得xy=﹣,
则P=﹣.
法二:由题可得,
解之得:,
∴P=xy=﹣,
故答案为:﹣.
【点睛】本题考查了完全平方公式,完全平方公式:(a±b)2=a2±2ab+b2.
14.已知(x2﹣x﹣1)x+2=1,则x= ﹣2或﹣1或0或2 .
【点拨】要使结果为1,可分为三种情况:①当指数是0时,②当底数为1时,③当底数为(﹣1)时,分别求出x即可得出答案.
【解析】解:①当x+2=0,即x=﹣2时,x2﹣x﹣1≠0,
∴x=﹣2,成立;
②当x2﹣x﹣1=1时,
解得:x=2或﹣1,
∴x=2或﹣1,成立;
③当x2﹣x﹣1=﹣1时,
解得:x=0或1,
当x=0时,(﹣1)2=1,成立,
当x=1时,(﹣1)3=﹣1,不成立,
故答案为:﹣2或﹣1或0或2.
【点睛】本题考查了零指数幂和有理数的乘方,掌握零指数幂的意义,有理数乘方的意义是解决问题的关键.
15.如图,从边长为(a+4)cm的正方形纸片中剪去一个边长为(a+1)cm的正方形(a>0),剩余部分沿虚线又剪拼成一个长方形(不重叠无缝隙),则矩形的周长为 (4a+16)cm .
【点拨】根据图形可得所拼矩形的长为[(a+4)+(a+1)]cm,宽为[(a+4)﹣(a+1)]cm,从而可计算出此题结果.
【解析】解:由题意得,所拼矩形的周长为:
2[(a+4)+(a+1)+(a+4)﹣(a+1)]
=2(2a+5+3)
=2(2a+8)
=(4a+16)cm,
故答案为:(4a+16)cm.
【点睛】此题考查了整式运算几何背景问题的解决能力,关键是能根据图形准确列式并计算.
16.我们知道下面的结论:若am=an(a>0,且a≠1),则m=n.利用这个结论解决下列问题:设2m=3,2n=6,2p=12.现给出m,n,p三者之间的三个关系式:①m+p=2n,②m+n=2p﹣3,③n+p=4m.其中正确的是 ①② .(填编号)
【点拨】由2n=6=2×3=2×2m=2m+1,得出n=m+1,由2p=12=22×3=22×2m=2m+2,得出p=m+2,进而得出p=n+1,进一步对m+p,m+n,n+p代入计算,即可得出答案.
【解析】解:∵2n=6=2×3=2×2m=2m+1,
∴n=m+1,
∵2p=12=22×3=22×2m=2m+2,
∴p=m+2,
∴p=n+1,
∴m+p=m+n+1=n+n=2n,
∴①符合题意;
∵m+n=p﹣2+p﹣1=2p﹣3,
∴②符合题意;
∵n+p=m+1+m+2=2m+3≠4m,
∴③不符合题意,
故答案为:①②.
【点睛】本题考查了幂的乘方与积的乘方,掌握幂的乘方与积的乘方的法则,同底数幂的乘法法则是解决问题的关键.
三.解答题
17.计算题:
(1)(﹣3a2b)2(2ab2)÷(﹣9a4b2).
(2)(2a+b)(b﹣2a)﹣(a﹣3b)2.
(3)(m﹣2n+3)(m+2n﹣3).
(4)20182﹣2017×2019(用乘法公式计算).
(5)化简求值:[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x,其中x=﹣2,y=1.
【点拨】(1)先算乘方,再算乘法,即可解答;
(2)利用平方差公式,完全平方公式进行计算即可解答;
(3)利用平方差公式,完全平方公式进行计算即可解答;
(4)利用平方差公式,进行计算即可解答;
(5)先去小括号,再去中括号,然后合并同类项,最后把x,y的值代入化简后的式子进行计算即可解答.
【解析】解:(1)(﹣3a2b)2(2ab2)÷(﹣9a4b2)
=9a4b2 2ab2÷(﹣9a4b2)
=18a5b4÷(﹣9a4b2)
=﹣2ab2;
(2)(2a+b)(b﹣2a)﹣(a﹣3b)2
=b2﹣4a2﹣a2+6ab﹣9b2
=﹣8b2﹣5a2+6ab;
(3)(m﹣2n+3)(m+2n﹣3)
=[m﹣(2n﹣3)][m+(2n﹣3)]
=m2﹣(2n﹣3)2
=m2﹣4n2+12n﹣9;
(4)20182﹣2017×2019
=20182﹣(2018﹣1)(2018+1)
=20182﹣20182+1
=1;
(5)[(x+2y)2﹣(x+y)(3x﹣y)﹣5y2]÷2x
=(x2+4xy+4y2﹣3x2﹣2xy+y2﹣5y2)÷2x
=(﹣2x2+2xy)÷2x
=﹣x+y,
当x=﹣2,y=1时,原式=﹣(﹣2)+1=3.
【点睛】本题考查了整式的混合运算﹣化简求值,准确熟练地进行计算是解题的关键.
18.用简便方法计算.
(1)186.72﹣2×186.7×86.7+86.72;
(2)(3+1)(32+1)(34+1)(38+1).
【点拨】(1)根据完全平方公式将原式化为(186.7﹣86.7)2即可;
(2)配上因式(3﹣1),连续使用平方差公式进行计算即可.
【解析】解:(1)原式=(186.7﹣86.7)2=1002=10000;
(2)原式=(3﹣1)(3+1)(32+1)(34+1)(38+1)
=(32﹣1)(32+1)(34+1)(38+1)
=(34﹣1)(34+1)(38+1)
=(38﹣1)(38+1)
=(316﹣1)
=.
【点睛】本题考查平方差公式、完全平方公式,掌握完全平方公式、平方差公式的结构特征是正确解答的前提.
19.先化简,再求值
(1)已知2x+y=1,求代数式(y+1)2﹣(y2﹣4x+4)的值.
(2)已知n为正整数,且x2n=4,求(x3n)2﹣2(x2)2n的值.
(3)若x、y满足,,求下列各式的值.
①(x+y)2;
②x4+y4.
【点拨】(1)根据完全平方公式化简后,再把2x+y=1代入计算即可;
(2)根据幂的乘方的运算法则化简后,把x2n=4代入计算即可;
(3)根据完全平方公式求解即可.
【解析】解:(1)∵2x+y=1,
∴(y+1)2﹣(y2﹣4x+4)
=y2+2y+1﹣y2+4x﹣4
=4x+2y﹣3
=2(2x+y)﹣3
=2﹣3
=﹣1;
(2)∵x2n=4,
∴(x3n)2﹣2(x2)2n=(x2n)3﹣2(22n)2=43﹣2×42=64﹣2×16=32;
(3)①∵,,
∴(x+y)2=x2+y2+2xy===;
②∵,,
∴x4+y4=(x2+y2)2﹣2x2y2===.
【点睛】本题主要考查了整式的混合运算,幂的乘方以及完全平方公式,熟记相关公式与运算法则是解答本题的关键.
20.定义一种新运算:观察下列各式:
1⊙3=1×4+3=7;3⊙(﹣1)=3×4﹣1=11;5⊙4=5×4+4=24;4⊙(﹣3)=4×4﹣3=13.
(1)请你想一想:a⊙b= 4a+b ;
(2)若a≠b,那么a⊙b ≠ b⊙a(填“=”或“≠”);
(3)先化简,再求值:(a﹣b)⊙(2a+b),其中a=1,b=2.
【点拨】(1)根据题目中的新运算,可以求出结果;
(2)根据(1)的结果和b⊙a结果比较;
(3)根据新运算将式子化简,然后代入a,b的值即可求出所得之值.
【解析】解:(1)a⊙b=4a+b.
故答案为:4a+b.
(2)a⊙b=4a+b,b⊙a=4b+a,
∵a≠b,
∴a⊙b≠b⊙a.
故答案为:≠
(3)(a﹣b)⊙(2a+b)
=4(a﹣b)+(2a+b)
=4a﹣4b+2a+b
=6a﹣3b.
当a=1,b=2时,原式=6×1﹣3×2=0.
【点睛】考查整式的化简求值,解决本题的关键是明确整式混合运算的计算方法.
21.如图,边长为a的大正方形有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)上述操作能验证的等式是: D (请选择正确的选项);
A.a2﹣ab=a(a﹣b) B.a2﹣2ab+b2=(a﹣b)2
C.a2+ab=a(a+b) D.a2﹣b2=(a+b)(a﹣b)
(2)请利用你从(1)选出的等式,完成下列各题:
①已知9a2﹣b2=36,3a+b=9,则3a﹣b= 4 ;
②计算:.
【点拨】(1)图1阴影部分的面积可以看作两个正方形的面积差,即a2﹣b2,图2阴影部分是长为a+b,宽为a﹣b的长方形,可表示其面积,由两种方法所求的面积相等可得答案;
(2)①根据平方差公式将9a2﹣b2=36转化为(3a+b)(3a﹣b)=36,再根据3a+b=9,进而求出3a﹣b的值;
②利用平方差公式将原式化为(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+),进而得出××××××××…××即可.
【解析】解:(1)图1阴影部分的面积可以看作两个正方形的面积差,即a2﹣b2,
图2阴影部分是长为a+b,宽为a﹣b的长方形,因此面积为(a+b)(a﹣b),
由图1、图2的面积相等得,a2﹣b2=(a+b)(a﹣b),
故答案为:D;
(2)①∵9a2﹣b2=36,
∴(3a+b)(3a﹣b)=36,
又∵3a+b=9,
∴3a﹣b=36÷9=4,
故答案为:4;
②原式=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)
=××××××××…××
=×
=.
【点睛】本题考查完全平方公式的几何背景,掌握完全平方公式的结构特征是正确解答的前提.
22.两个边长分别为m和n的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若在图1中大正方形的右上角再摆放一个边长为n的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含m,n的代数式分别表示S1,S2;
(2)若m﹣n=10,mn=20,求S1+S2的值;
(3)若S1+S2=30,求图3中阴影部分的面积S3.
【点拨】(1)S1可以看作两个正方形的面积差,即S1=m2﹣n2,S2是长为2n﹣m,高为n的长方形的面积,即S2=(2n﹣m) n=2n2﹣mn;
(2)将S1+S2=m2﹣n2+2n2﹣mn,变形为(m﹣n)2+mn,再代入计算即可;
(3)由S1+S2=30,可得到m2+n2﹣mn=30,由图3看得出S3=(m2+n2﹣mn),整体代入计算即可.
【解析】解:(1)S1可以看作两个正方形的面积差,即S1=m2﹣n2,
S2是长为2n﹣m,高为n的长方形的面积,即S2=(2n﹣m) n=2n2﹣mn;
(2)∵m﹣n=10,mn=20,
∴S1+S2=m2﹣n2+2n2﹣mn
=m2+n2﹣mn
=(m﹣n)2+mn
=100+20
=120;
(3)∵S1+S2=m2+n2﹣mn=30,
∴S3=m2+n2﹣m2﹣n(m+n)
=m2﹣mn+n2
=(m2+n2﹣mn)
=×30
=15.
【点睛】本题考查完全平方公式的几何背景,掌握完全平方公式的结构特征是正确解答的前提.
23.已知x≠1.观察下列等式:
(1﹣x)(1+x)=1﹣x2;
(1﹣x)(1+x+x2)=1﹣x3;
(1﹣x)(1+x+x2+x3)=1﹣x4;
…
(1)猜想:(1﹣x)(1+x+x2+x3+…+xn﹣1)= 1﹣xn ;
(2)应用:根据你的猜想请你计算下列式子的值:
①(1﹣2)(1+2+22+23+24+25+26)= ﹣127 ;
②(x﹣1)(x2022+x2021+x2020+…+x2+x+1)= x2023﹣1 .
(3)判断2100+299+298+…+22+2+1的值的个位数是几?并说明你的理由.
【点拨】(1)根据所给的等式,不难得出结果;
(2)①利用(1)中的结论进行求解即可;
②利用(1)中的结论进行求解即可;
(3)先利用(1)的结论进行求解,再判断其个位数即可.
【解析】解:(1)∵(1﹣x)(1+x)=1﹣x2;
(1﹣x)(1+x+x2)=1﹣x3;
(1﹣x)(1+x+x2+x3)=1﹣x4
…
∴(1﹣x)(1+x+x2+x3+…+xn﹣1)=1﹣xn;
故答案为:1﹣xn;
(2)①(1﹣2)(1+2+22+23+24+25+26)
=1﹣27
=1﹣128
=﹣127;
故答案为:﹣127;
(2)②(x﹣1)(x2022+x2021+x2020+…+x2+x+1)
=﹣(1﹣x)(1+x+x2+…+x2022)
=﹣(1﹣x2023)
=x2023﹣1.
故答案为:x2023﹣1;
(3)1,理由如下:
2100+299+298+…+22+2+1
=﹣(1﹣2)×(1+2+22+…+2100)
=﹣(1﹣2101)
=2101﹣1.
∵21的个位数是2,
22的个位数是4,
23的个位数是8,
24的个位数是6,
25的个位数是2,
…
∴其个位数以2,4,8,6不断循环出现,
∵101÷4=25……1,
∴2101的个位数字是2,
∴2101﹣1的个位数是1.
【点睛】本题主要考查多项式乘多项式,数字的变化规律,解答的关键是对相应的运算法则的掌握.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
