3.2单项式的乘法 课件(共21张PPT)
文档属性
| 名称 | 3.2单项式的乘法 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-20 23:25:11 | ||
图片预览








文档简介
(共21张PPT)
3.2单项式的乘法
浙教版七年级下册
学习目标
1.掌握单项式与单项式相乘的法则,并通过学习能运用法则进行相关计算
1.掌握单项式与多项式相乘的法则,并能综合运用法则进行相关计算
复习导入
文字语言 符号语言
同底数幂相乘,
底数不变,指数相加。
其中m,n都是正整数
幂的乘方,
底数不变,指数相乘。
同底数幂的
乘法法则
幂的
乘方法则
积的
乘方法则
把积的每个因式分别乘方
再把所得的幂相乘.
活动3:举例: 该如何计算?运用到哪些知识?
新知导入
活动1:写一个只含a单项式
活动2:与同桌的单项式进行相乘,试着求出计算结果
乘法交换律和结合律
初步感受:单项式与单项式相乘时,可以从哪几个方面开展运算?
继续探究
计算:
乘法交换律和结合律
同底数幂的乘法法则
思考:单项式与单项式相乘时,可以从哪几个方面开展运算?
归纳整理
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式。
单项式与单项式相乘的法则(两乘一不变)
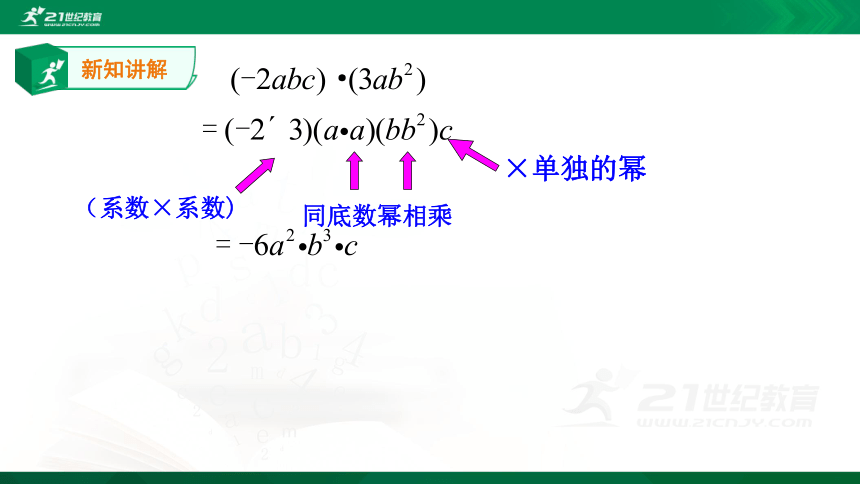
新知讲解
(系数×系数)
同底数幂相乘
×单独的幂
课堂练习
( )
( )
( )
( )
(1)
(2)
(3)
(4)
判断下列计算对错,错的请订正
6a5
-12x3y
整体思想
注意符号
注意指数运算
新知讲解
(1)3b3 b2
(2) (-6ay3)(-a2)
例1、计算
新知讲解
(3)(2×103)(4×104) 105
(4) -6a2(x-y)3 2a(x-y)2
单项式×单项式步骤
思考:如何开展计算更简便?
1、系数相乘
2、同底数幂相乘
3、只在一个单项式中出现的字母,则连同它的指数不变,作为积的一个因式。
注意运算符号
注意指数运算类型
不漏乘
细心算一算:
(1) 3x2·5x3 = (2) 4y· (-2xy2) =
(3) (-3x2y) ·(-4x) = (4) (-4a2b)(-2a) =
(5) 3y(-2x2y2) = (6) 3a3b·(-ab3c2) =
15X5
-8xy3
12x3y
8a3b
-6x2y3
-3a4b4c2
先算乘方,再算单项式相乘.
注意
课堂练习
探究
观察左图
问题1:请用两种不同的方法表示蓝色区域的面积。
a(b-2m)=ab-2am
=ab-am-am=ab-2am
a(b-2m)
ab-2am
问题2:这两种用不同方法表示的面积相等,
你能用运算律解释他的相等吗?
问题3:现在你能总结出单项式与多项式相乘的运算规律吗
a(b+c)=ab+ac
课堂小结
单项式乘以多项式的法则
一般地,单项式与多项式相乘,就是用单项式乘多项式的每一项,再把所得的积相加.
文字表述
符号表述
p (a + b+c) =
pa
pb
pc
+
+
例题讲解
例2 计算:
(1)2a2b(ab-3ab2); (2)(x-xy) (-12y)
解:(1)2a2b(ab-3ab2)
=2a2b ab+2a2b (-3ab2)
=a3b2-6a3b3;
(2)(x-xy) (-12y)
=x (-12y)+(-xy) (-12y)
=-4xy+9xy2
注意:1.乘积中每项的符号的确定:带上符号计算
2.乘积的项数:由多项式的项数决定
判断
(1)-3x(2x-3y)=-6x2-9xy ( )
(2)x(2x2-3x+1)=2x3-3x2 ( )
(3)am(am-a2+1)=a2m-a2m+am=am ( )
×
×
×
注意各项符号的确定
漏乘常数项
法则混淆
巩固练习
(4)3a2b 4a3=12a5 ( )
(3)(-7a) (-3a3) =-21a4 ( )
(2)6a3 5a2=11a5 ( )
(1)4a2 2a4 = 8a8 ( )
×
×
×
×
系数相乘
同底数幂的乘法,底数不变,指数相加
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
应注意符号
8a6
30a5
21a4
12a5 b
1.判断
当堂检测
挑战自我
2.计算5x(x2-2x+4)+x2(x+1)的结果是( )
A.6x3-10x2+20x B.5x3-11x2+20x
C.6x3-9x2+20x D.5x3-10x2+20x
3.计算:(-2x3y)·(3xy2-4xy+1)=___________________________.
C
-6x4y3+8x4y2-2x3y
拓展应用
解:原式=3x3y ·4y2-16x2y2· (-xy) -xy3·16x2
=12x3y3+16x3y3-16x3y3
=12x3y3
4.计算:3x3y·(-2y)2 -(-4xy)2·(-xy) -xy3·(-4x)2
单项式乘以单项式
转化
运用乘法的交换律、结合律
有理数的乘法
幂的乘法运算
单项式乘以多项式
转化
运用乘法分配律
单项式乘以单项式
课堂总结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.2单项式的乘法
浙教版七年级下册
学习目标
1.掌握单项式与单项式相乘的法则,并通过学习能运用法则进行相关计算
1.掌握单项式与多项式相乘的法则,并能综合运用法则进行相关计算
复习导入
文字语言 符号语言
同底数幂相乘,
底数不变,指数相加。
其中m,n都是正整数
幂的乘方,
底数不变,指数相乘。
同底数幂的
乘法法则
幂的
乘方法则
积的
乘方法则
把积的每个因式分别乘方
再把所得的幂相乘.
活动3:举例: 该如何计算?运用到哪些知识?
新知导入
活动1:写一个只含a单项式
活动2:与同桌的单项式进行相乘,试着求出计算结果
乘法交换律和结合律
初步感受:单项式与单项式相乘时,可以从哪几个方面开展运算?
继续探究
计算:
乘法交换律和结合律
同底数幂的乘法法则
思考:单项式与单项式相乘时,可以从哪几个方面开展运算?
归纳整理
单项式与单项式相乘,把它们的系数、同底数幂分别相乘,其余字母连同它的指数不变,作为积的因式。
单项式与单项式相乘的法则(两乘一不变)
新知讲解
(系数×系数)
同底数幂相乘
×单独的幂
课堂练习
( )
( )
( )
( )
(1)
(2)
(3)
(4)
判断下列计算对错,错的请订正
6a5
-12x3y
整体思想
注意符号
注意指数运算
新知讲解
(1)3b3 b2
(2) (-6ay3)(-a2)
例1、计算
新知讲解
(3)(2×103)(4×104) 105
(4) -6a2(x-y)3 2a(x-y)2
单项式×单项式步骤
思考:如何开展计算更简便?
1、系数相乘
2、同底数幂相乘
3、只在一个单项式中出现的字母,则连同它的指数不变,作为积的一个因式。
注意运算符号
注意指数运算类型
不漏乘
细心算一算:
(1) 3x2·5x3 = (2) 4y· (-2xy2) =
(3) (-3x2y) ·(-4x) = (4) (-4a2b)(-2a) =
(5) 3y(-2x2y2) = (6) 3a3b·(-ab3c2) =
15X5
-8xy3
12x3y
8a3b
-6x2y3
-3a4b4c2
先算乘方,再算单项式相乘.
注意
课堂练习
探究
观察左图
问题1:请用两种不同的方法表示蓝色区域的面积。
a(b-2m)=ab-2am
=ab-am-am=ab-2am
a(b-2m)
ab-2am
问题2:这两种用不同方法表示的面积相等,
你能用运算律解释他的相等吗?
问题3:现在你能总结出单项式与多项式相乘的运算规律吗
a(b+c)=ab+ac
课堂小结
单项式乘以多项式的法则
一般地,单项式与多项式相乘,就是用单项式乘多项式的每一项,再把所得的积相加.
文字表述
符号表述
p (a + b+c) =
pa
pb
pc
+
+
例题讲解
例2 计算:
(1)2a2b(ab-3ab2); (2)(x-xy) (-12y)
解:(1)2a2b(ab-3ab2)
=2a2b ab+2a2b (-3ab2)
=a3b2-6a3b3;
(2)(x-xy) (-12y)
=x (-12y)+(-xy) (-12y)
=-4xy+9xy2
注意:1.乘积中每项的符号的确定:带上符号计算
2.乘积的项数:由多项式的项数决定
判断
(1)-3x(2x-3y)=-6x2-9xy ( )
(2)x(2x2-3x+1)=2x3-3x2 ( )
(3)am(am-a2+1)=a2m-a2m+am=am ( )
×
×
×
注意各项符号的确定
漏乘常数项
法则混淆
巩固练习
(4)3a2b 4a3=12a5 ( )
(3)(-7a) (-3a3) =-21a4 ( )
(2)6a3 5a2=11a5 ( )
(1)4a2 2a4 = 8a8 ( )
×
×
×
×
系数相乘
同底数幂的乘法,底数不变,指数相加
只在一个单项式里含有的字母,要连同它的指数写在积里,防止遗漏.
应注意符号
8a6
30a5
21a4
12a5 b
1.判断
当堂检测
挑战自我
2.计算5x(x2-2x+4)+x2(x+1)的结果是( )
A.6x3-10x2+20x B.5x3-11x2+20x
C.6x3-9x2+20x D.5x3-10x2+20x
3.计算:(-2x3y)·(3xy2-4xy+1)=___________________________.
C
-6x4y3+8x4y2-2x3y
拓展应用
解:原式=3x3y ·4y2-16x2y2· (-xy) -xy3·16x2
=12x3y3+16x3y3-16x3y3
=12x3y3
4.计算:3x3y·(-2y)2 -(-4xy)2·(-xy) -xy3·(-4x)2
单项式乘以单项式
转化
运用乘法的交换律、结合律
有理数的乘法
幂的乘法运算
单项式乘以多项式
转化
运用乘法分配律
单项式乘以单项式
课堂总结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
