3.4 乘法公式(1) 课件(共19张PPT)
文档属性
| 名称 | 3.4 乘法公式(1) 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-23 21:40:14 | ||
图片预览






文档简介
(共19张PPT)
3.4 乘法公式(1)
浙教版七年级下册
学习目标
1.通过多项式与多项式相乘的法则,探究特殊的多项式与多项式相乘的法则
3.经历观察、分析、归纳,体验数学学习中一般到特殊的数学思想
2.掌握乘法公式中的平方差公式并运用解决问题
复习导入
(2x + y)(x y)
计算
=2x2 -2xy+xy y2
=2x2 -xy y2
再计算:
(a+1)(a-1)
(x+3)(x-3)
(m+4)(m-4)
=a2 -1
=x2 -9
=m2 16
观察上述算式与计算结果,有什么规律吗?
(a+b) (a-b) = a2 -b2
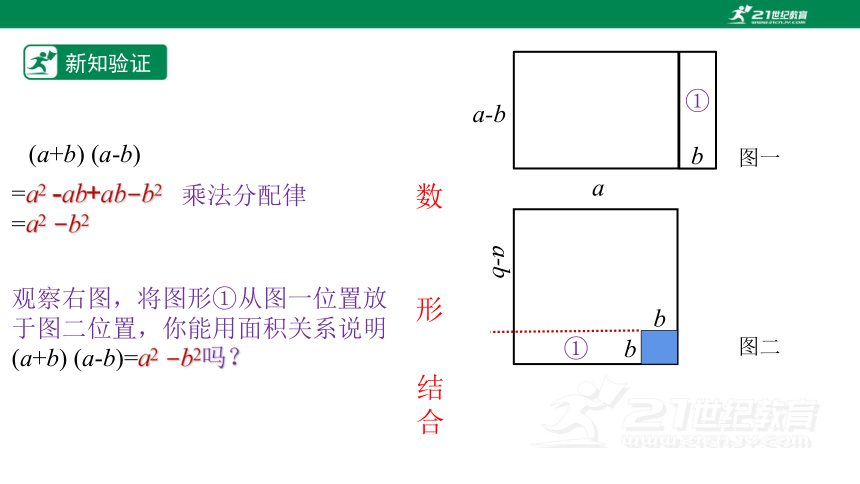
新知验证
(a+b) (a-b)
=a2 -ab+ab-b2
=a2 -b2
乘法分配律
观察右图,将图形①从图一位置放于图二位置,你能用面积关系说明
(a+b) (a-b)=a2 -b2吗?
图一
图二
a-b
a
b
a-b
b
b
①
①
数
形
结
合
归纳整理
(a+b) (a-b)=a2 -b2
平方差公式
符号语言
文字语言
两数和
与两数差=
这两数的平方差
观察公式,满足什么特征的多项式相乘,可用平方差公式呢?
左式特征:
右式结果:
(相同项)2-(相反项)2
小试牛刀
1.选择:下列各式中,能用平方差公式的是( ) A. (x-3)(-x+3) B.(x+2y)(2x-y)
C. (y-1)(-y-1) D.(y+1)(-y-1)
2.下列多项式乘法中,能用平方差公的是 。
(1) (x+1)(1+x) (2) (a+b)(b-a)
(3) (-a+b)(a-b) (4) (x2-y)(x+y2)
(5) (-a-b)(a-b) (6) (c2-d2)(d2+c2)
c
(2)(4)(6)
注:这里的两数可以是数字、字母、单项式也可以是两个多项式等.
填一填
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
新知讲解
例1 运用平方差公式计算:
=(3x)2-(5y)2
=9x2-25y2
=(b)2-a2
=b2-a2
拓展提升
例2 用平方差公式计算:
=(100+3)2-(100-3)2
=1002-32
=9991
=(60-0.2)2-(60+0.2)2
=602-0.22
=3599.96
思考:根据题目要求,如何将乘法算式转化成符合平方差公式的算式?试一试。
方法:计算原算式中两数的平均值作为公式中的a
课堂练习
1.用平方差公式计算
(1)(2-a)(2+a)
(2)(x + )(x - )
(1)102×98
(1)50.5×49.5
=4-a2
=x2- y2
=(100+2)2-(100-2)2=1002-32=9996
=(50+0.5)2-(50+0.5)2
=502-0.52
=2499.75
拓展提升
1.用平方差公式计算
(1)(-m+11)(-m-11)
(2)(-4x+)(y +4x)
(1)(2b+a)(a-2b)
(1)(-m-n)(m-n)
=m2-121
=y2- 16x2
=a2- 4b2
=n2- m2
拓展提升
2.在括号内填入怎样的代数式,才能直接运用平方差公式进行计算?
思考:平方差公式中的字母 可表示什么?
代数式.
拓展提升
3、再次利用平方差公式计算:
(1) 20222 - 2021×2023.
(2) (2+1)(22+1)(24+1)(28+1)+1
=20222-(2022-1)(2022+1)
=20222-(20222-1)
=1
=(2-1)(2+1)(22+1)(24+1)(28+1)+1
=(22-1)(22+1)(24+1)(28+1)+1
=......
=216
构建思想
这里有什么经验可借鉴?
思考:观察括号里的式子,有什么规律吗?说一说
知识迁移
(2+1)(22+1)(24+1)(28+1)+1
=(2-1)(2+1)(22+1)(24+1)(28+1)+1
类比上题的思路,你会如何展开计算?
(3-1)
直接乘以
可以吗?
小结:自主添项后要保持原式结果不改变,否则要添上一对互为倒数的数
=(3-1)(3+1)(32+1)(34+1)(38+1)
=(32-1)(32+1)(34+1)(38+1)
。。。。。。
=(38-1)(38+1)
=
课堂总结
一个公式 (a+b)(a-b)=a2-b2
(1)简化某些多项式的乘法运算
(2)提供有理数乘法的速算方法
两种作用
三个关注
(1)要符合公式特征才能运用平方差公式
(2)公式中的a、b可以代表数字、字母或者式子(3)注意实质,善用变形创造条件用平方差公式
(相同项)2-(相反项)2
1.利用平方差公式计算
(1) ( x+2 ) ( x-2 )
(2) (1+3a) (1-3a)
(3) (x+5y) (x-5y)
(4) (-m+n) (-m-n)
当堂检测
1.利用平方差公式计算
(1) ( x+2 ) ( x-2 )
(2) (1+3a) (1-3a)
(3) (x+5y) (x-5y)
(4) (-m+n) (-m-n)
=x2-4
=1-9a2
=x2-25y2
=m2-n2
2.利用平方差公式计算
(1) (-2x2 + 5)(-2x2 -5 )
(2) (-4a-1) (1-4a)
(3)(ab+8)(ab-8)
=4x4-25
=16a2-1
=a2b2-64
当堂检测
4、利用平方差公式计算:
(1) (a-2)(a+2)(a2 + 4);
解:原式=(a2-4)(a2+4)
=a4-16;
(2) (x-y)(x+y)(x2+y2)(x4+y4).
原式=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
3.4 乘法公式(1)
浙教版七年级下册
学习目标
1.通过多项式与多项式相乘的法则,探究特殊的多项式与多项式相乘的法则
3.经历观察、分析、归纳,体验数学学习中一般到特殊的数学思想
2.掌握乘法公式中的平方差公式并运用解决问题
复习导入
(2x + y)(x y)
计算
=2x2 -2xy+xy y2
=2x2 -xy y2
再计算:
(a+1)(a-1)
(x+3)(x-3)
(m+4)(m-4)
=a2 -1
=x2 -9
=m2 16
观察上述算式与计算结果,有什么规律吗?
(a+b) (a-b) = a2 -b2
新知验证
(a+b) (a-b)
=a2 -ab+ab-b2
=a2 -b2
乘法分配律
观察右图,将图形①从图一位置放于图二位置,你能用面积关系说明
(a+b) (a-b)=a2 -b2吗?
图一
图二
a-b
a
b
a-b
b
b
①
①
数
形
结
合
归纳整理
(a+b) (a-b)=a2 -b2
平方差公式
符号语言
文字语言
两数和
与两数差=
这两数的平方差
观察公式,满足什么特征的多项式相乘,可用平方差公式呢?
左式特征:
右式结果:
(相同项)2-(相反项)2
小试牛刀
1.选择:下列各式中,能用平方差公式的是( ) A. (x-3)(-x+3) B.(x+2y)(2x-y)
C. (y-1)(-y-1) D.(y+1)(-y-1)
2.下列多项式乘法中,能用平方差公的是 。
(1) (x+1)(1+x) (2) (a+b)(b-a)
(3) (-a+b)(a-b) (4) (x2-y)(x+y2)
(5) (-a-b)(a-b) (6) (c2-d2)(d2+c2)
c
(2)(4)(6)
注:这里的两数可以是数字、字母、单项式也可以是两个多项式等.
填一填
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
新知讲解
例1 运用平方差公式计算:
=(3x)2-(5y)2
=9x2-25y2
=(b)2-a2
=b2-a2
拓展提升
例2 用平方差公式计算:
=(100+3)2-(100-3)2
=1002-32
=9991
=(60-0.2)2-(60+0.2)2
=602-0.22
=3599.96
思考:根据题目要求,如何将乘法算式转化成符合平方差公式的算式?试一试。
方法:计算原算式中两数的平均值作为公式中的a
课堂练习
1.用平方差公式计算
(1)(2-a)(2+a)
(2)(x + )(x - )
(1)102×98
(1)50.5×49.5
=4-a2
=x2- y2
=(100+2)2-(100-2)2=1002-32=9996
=(50+0.5)2-(50+0.5)2
=502-0.52
=2499.75
拓展提升
1.用平方差公式计算
(1)(-m+11)(-m-11)
(2)(-4x+)(y +4x)
(1)(2b+a)(a-2b)
(1)(-m-n)(m-n)
=m2-121
=y2- 16x2
=a2- 4b2
=n2- m2
拓展提升
2.在括号内填入怎样的代数式,才能直接运用平方差公式进行计算?
思考:平方差公式中的字母 可表示什么?
代数式.
拓展提升
3、再次利用平方差公式计算:
(1) 20222 - 2021×2023.
(2) (2+1)(22+1)(24+1)(28+1)+1
=20222-(2022-1)(2022+1)
=20222-(20222-1)
=1
=(2-1)(2+1)(22+1)(24+1)(28+1)+1
=(22-1)(22+1)(24+1)(28+1)+1
=......
=216
构建思想
这里有什么经验可借鉴?
思考:观察括号里的式子,有什么规律吗?说一说
知识迁移
(2+1)(22+1)(24+1)(28+1)+1
=(2-1)(2+1)(22+1)(24+1)(28+1)+1
类比上题的思路,你会如何展开计算?
(3-1)
直接乘以
可以吗?
小结:自主添项后要保持原式结果不改变,否则要添上一对互为倒数的数
=(3-1)(3+1)(32+1)(34+1)(38+1)
=(32-1)(32+1)(34+1)(38+1)
。。。。。。
=(38-1)(38+1)
=
课堂总结
一个公式 (a+b)(a-b)=a2-b2
(1)简化某些多项式的乘法运算
(2)提供有理数乘法的速算方法
两种作用
三个关注
(1)要符合公式特征才能运用平方差公式
(2)公式中的a、b可以代表数字、字母或者式子(3)注意实质,善用变形创造条件用平方差公式
(相同项)2-(相反项)2
1.利用平方差公式计算
(1) ( x+2 ) ( x-2 )
(2) (1+3a) (1-3a)
(3) (x+5y) (x-5y)
(4) (-m+n) (-m-n)
当堂检测
1.利用平方差公式计算
(1) ( x+2 ) ( x-2 )
(2) (1+3a) (1-3a)
(3) (x+5y) (x-5y)
(4) (-m+n) (-m-n)
=x2-4
=1-9a2
=x2-25y2
=m2-n2
2.利用平方差公式计算
(1) (-2x2 + 5)(-2x2 -5 )
(2) (-4a-1) (1-4a)
(3)(ab+8)(ab-8)
=4x4-25
=16a2-1
=a2b2-64
当堂检测
4、利用平方差公式计算:
(1) (a-2)(a+2)(a2 + 4);
解:原式=(a2-4)(a2+4)
=a4-16;
(2) (x-y)(x+y)(x2+y2)(x4+y4).
原式=(x2-y2)(x2+y2)(x4+y4)
=(x4-y4)(x4+y4)
=x8-y8.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
