2022-2023学年浙教版七年级数学下册1.3平行线的判定同步练习(无答案)
文档属性
| 名称 | 2022-2023学年浙教版七年级数学下册1.3平行线的判定同步练习(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 198.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-13 19:10:52 | ||
图片预览

文档简介
平行线的判定
命题点1:平行线的判定定理应用
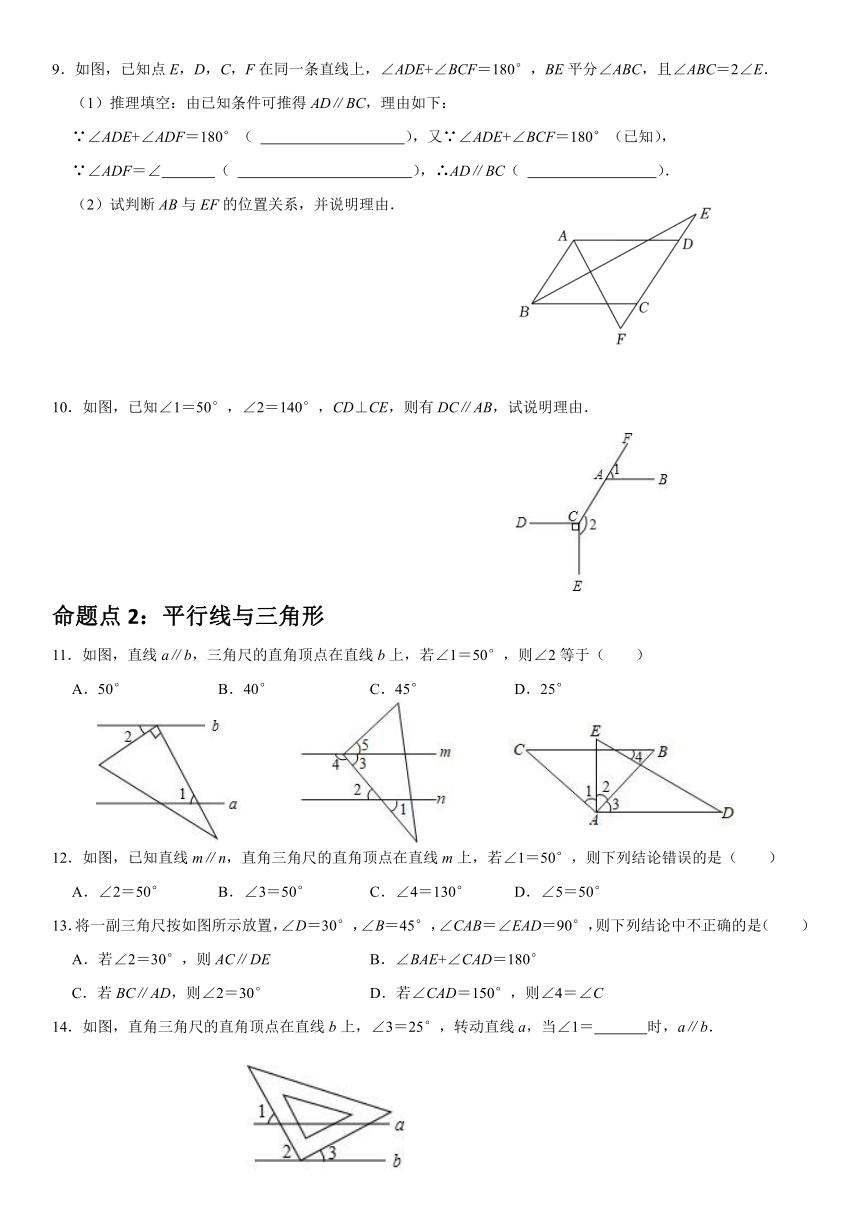
1.如图是一张四边形纸片ABCD,以下测量方法能判定AD∥BC的是( )
A.AB⊥BC,AB⊥AD B.AB⊥BC,CD⊥BC
C.AB⊥BC,CD⊥AD D.AB=CD
2.如图,已知∠1=∠2,其中能判定AB∥CD的是( )
A. B. C. D.
3.如图为平面上五条直线l1,l2,l3,l4,l5相交的情形,根据图中标示的角度,下列叙述正确的是( )
A.l1和l3平行,l2和l3平行 B.l1和l3平行,l2和l3不平行
C.l2和l3平行,l4和l5不平行 D.l2和l3平行,l4和l5平行
4.如图,下列条件中,能判定a∥b的是( )
A.∠1=∠2 B.∠1=∠4 C.∠1+∠3=180° D.∠3+∠4=180°
5.对于图中标记的各角,下列条件能够推理得到a∥b的是( )
A.∠2=∠4 B.∠3+∠4=180° C.∠1+∠4=180° D.∠1=∠4
6.如图,下列条件中,可得到AD∥BC的是( )
①AC⊥AD,AC⊥BC;②∠1=∠2,∠3=∠D;③∠4=∠5;④∠BAD+∠ABC=180°.
A.①②③ B.②③④ C.①②④ D.①③④
7.如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是 .
8.如图,点E在AC的延长线上,对于给出的四个条件:
(1)∠3=∠4;(2)∠1=∠2;(3)∠A=∠DCE;(4)∠D+∠ABD=180°.能判断AB∥CD的有 个.
9.如图,已知点E,D,C,F在同一条直线上,∠ADE+∠BCF=180°,BE平分∠ABC,且∠ABC=2∠E.
(1)推理填空:由已知条件可推得AD∥BC,理由如下:
∵∠ADE+∠ADF=180°( ),又∵∠ADE+∠BCF=180°(已知),
∵∠ADF=∠ ( ),∴AD∥BC( ).
(2)试判断AB与EF的位置关系,并说明理由.
10.如图,已知∠1=50°,∠2=140°,CD⊥CE,则有DC∥AB,试说明理由.
命题点2:平行线与三角形
11.如图,直线a∥b,三角尺的直角顶点在直线b上,若∠1=50°,则∠2等于( )
A.50° B.40° C.45° D.25°
12.如图,已知直线m∥n,直角三角尺的直角顶点在直线m上,若∠1=50°,则下列结论错误的是( )
A.∠2=50° B.∠3=50° C.∠4=130° D.∠5=50°
13.将一副三角尺按如图所示放置,∠D=30°,∠B=45°,∠CAB=∠EAD=90°,则下列结论中不正确的是( )
A.若∠2=30°,则AC∥DE B.∠BAE+∠CAD=180°
C.若BC∥AD,则∠2=30° D.若∠CAD=150°,则∠4=∠C
14.如图,直角三角尺的直角顶点在直线b上,∠3=25°,转动直线a,当∠1= 时,a∥b.
15.已知直线a⊥b,垂足为O,将一块含45°角的直角三角尺ABC按如图①所示的方式放置,其中直角顶点C在直线a上,A、B两点在直线b上,将三角尺绕点O顺时针旋转α(0<α<180°,且α≠90°,α≠135°),如图②,在旋转的过程中,AC所在直线与a相交于点E,BC所在直线与b相交于点F.
(1)若α=60°,则∠CEO+∠CFO= °;
(2)若EM平分∠CEO,FN平分∠CFO,判断EM与FN的位置关系,并说明理由.
16.数学兴趣小组活动中,小明将等腰直角三角板放到印有等宽的平行线的作业纸上,如图1,l∥m∥n,三角板的直角顶点A落在直线m上,直角边AB与直线l相交于点D,直角边AC与直线n相交于点E,斜边BC分别与直线l,m,n相交于点F,G,H.
(1)当∠BDF=35°时,∠CAG= °;当∠BDF=20°时,∠CAG= °;
(2)请从下列的A,B两题中任选一题作答,我选择 题.
A:如图1,若∠BDF=α(0°<α<90°),求∠CAG的度数(用含α的式子表示)
B:如图2,连接GE,若∠GEH+∠AEH=180°,则∠GEH与∠BDF有什么数量关系?说明理由.
命题点3:平行线综合应用
17.完成下面推理过程.在括号内的横线上填空或填上推理依据
如图,已知:∠3=∠BAE,AC⊥BE,∠1=∠2,∠3+∠4=180°,求证:AB∥CD,AD∥BE
证明:∵AC⊥BE(已知);
∴∠3=90° ;∴∠BAE=∠3=90°;又∵∠3+∠4=180°(已知);
∴∠4=180°﹣∠3=90°;∴∠ =∠BAE ;∴AB∥CD ;
∵∠1=∠2(已知);∴∠1+∠CAE=∠2+∠CAE ;
即∠BAE=∠CAD;∴∠3=∠CAD;∴AD∥BE .
18.已知:如图,∠1=∠2,∠3=∠4.请说明DF∥BC的理由.
19.如图,GM、HN分别平分∠BGE和∠DHF,且∠1+∠2=90°,求证:AB∥CD.
20.小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD、MF的位置关系是 ;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线上一点,则BD、MF的位置关系是 ;
(2)请就(1)中图①的情况写出证明过程.
21.如图1,已知三角形ABC与三角形ADE摆放在一起,点A、C、E在同一直线上,其中∠ACB=30°,∠DAE=45°,∠BAC=∠D=90°.如图2,固定三角形ABC,将三角形ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).
(1)当α为 度时,AD∥BC;
(2)在旋转过程中,试探究∠CAD与∠BAE之间的关系;
(3)当三角形ADE的一边与三角形ABC的某一边平行(不共线)时,直接写出旋转角α所有可能的度数(第(1)题的结论除外).
22.如图,直线PQ∥MN,一副三角板(∠ABC=∠CDE=90°,∠ACB=30°,∠BAC=60°,∠DCE=∠DEC=45°)按如图①放置,其中点E在直线PQ上,点B,C均在直线MN上,且CE平分∠ACN.
(1)求∠DEQ的度数;
(2)如图②,若将△ABC绕B点以每秒5°的速度按逆时针方向旋转(A,C的对应点分别为F,G).设旋转时间为t秒(0≤t≤36).
①在旋转过程中,若边BG∥CD,求t的值;
②若在△ABC绕B点旋转的同时,△CDE绕E点以每秒4°的速度按顺时针方向旋转(C,D的对应点分别为H,K).请直接写出当边BG∥HK时t的值.
命题点1:平行线的判定定理应用
1.如图是一张四边形纸片ABCD,以下测量方法能判定AD∥BC的是( )
A.AB⊥BC,AB⊥AD B.AB⊥BC,CD⊥BC
C.AB⊥BC,CD⊥AD D.AB=CD
2.如图,已知∠1=∠2,其中能判定AB∥CD的是( )
A. B. C. D.
3.如图为平面上五条直线l1,l2,l3,l4,l5相交的情形,根据图中标示的角度,下列叙述正确的是( )
A.l1和l3平行,l2和l3平行 B.l1和l3平行,l2和l3不平行
C.l2和l3平行,l4和l5不平行 D.l2和l3平行,l4和l5平行
4.如图,下列条件中,能判定a∥b的是( )
A.∠1=∠2 B.∠1=∠4 C.∠1+∠3=180° D.∠3+∠4=180°
5.对于图中标记的各角,下列条件能够推理得到a∥b的是( )
A.∠2=∠4 B.∠3+∠4=180° C.∠1+∠4=180° D.∠1=∠4
6.如图,下列条件中,可得到AD∥BC的是( )
①AC⊥AD,AC⊥BC;②∠1=∠2,∠3=∠D;③∠4=∠5;④∠BAD+∠ABC=180°.
A.①②③ B.②③④ C.①②④ D.①③④
7.如图,将木条a,b与c钉在一起,∠1=70°,∠2=50°,要使木条a与b平行,木条a旋转的度数至少是 .
8.如图,点E在AC的延长线上,对于给出的四个条件:
(1)∠3=∠4;(2)∠1=∠2;(3)∠A=∠DCE;(4)∠D+∠ABD=180°.能判断AB∥CD的有 个.
9.如图,已知点E,D,C,F在同一条直线上,∠ADE+∠BCF=180°,BE平分∠ABC,且∠ABC=2∠E.
(1)推理填空:由已知条件可推得AD∥BC,理由如下:
∵∠ADE+∠ADF=180°( ),又∵∠ADE+∠BCF=180°(已知),
∵∠ADF=∠ ( ),∴AD∥BC( ).
(2)试判断AB与EF的位置关系,并说明理由.
10.如图,已知∠1=50°,∠2=140°,CD⊥CE,则有DC∥AB,试说明理由.
命题点2:平行线与三角形
11.如图,直线a∥b,三角尺的直角顶点在直线b上,若∠1=50°,则∠2等于( )
A.50° B.40° C.45° D.25°
12.如图,已知直线m∥n,直角三角尺的直角顶点在直线m上,若∠1=50°,则下列结论错误的是( )
A.∠2=50° B.∠3=50° C.∠4=130° D.∠5=50°
13.将一副三角尺按如图所示放置,∠D=30°,∠B=45°,∠CAB=∠EAD=90°,则下列结论中不正确的是( )
A.若∠2=30°,则AC∥DE B.∠BAE+∠CAD=180°
C.若BC∥AD,则∠2=30° D.若∠CAD=150°,则∠4=∠C
14.如图,直角三角尺的直角顶点在直线b上,∠3=25°,转动直线a,当∠1= 时,a∥b.
15.已知直线a⊥b,垂足为O,将一块含45°角的直角三角尺ABC按如图①所示的方式放置,其中直角顶点C在直线a上,A、B两点在直线b上,将三角尺绕点O顺时针旋转α(0<α<180°,且α≠90°,α≠135°),如图②,在旋转的过程中,AC所在直线与a相交于点E,BC所在直线与b相交于点F.
(1)若α=60°,则∠CEO+∠CFO= °;
(2)若EM平分∠CEO,FN平分∠CFO,判断EM与FN的位置关系,并说明理由.
16.数学兴趣小组活动中,小明将等腰直角三角板放到印有等宽的平行线的作业纸上,如图1,l∥m∥n,三角板的直角顶点A落在直线m上,直角边AB与直线l相交于点D,直角边AC与直线n相交于点E,斜边BC分别与直线l,m,n相交于点F,G,H.
(1)当∠BDF=35°时,∠CAG= °;当∠BDF=20°时,∠CAG= °;
(2)请从下列的A,B两题中任选一题作答,我选择 题.
A:如图1,若∠BDF=α(0°<α<90°),求∠CAG的度数(用含α的式子表示)
B:如图2,连接GE,若∠GEH+∠AEH=180°,则∠GEH与∠BDF有什么数量关系?说明理由.
命题点3:平行线综合应用
17.完成下面推理过程.在括号内的横线上填空或填上推理依据
如图,已知:∠3=∠BAE,AC⊥BE,∠1=∠2,∠3+∠4=180°,求证:AB∥CD,AD∥BE
证明:∵AC⊥BE(已知);
∴∠3=90° ;∴∠BAE=∠3=90°;又∵∠3+∠4=180°(已知);
∴∠4=180°﹣∠3=90°;∴∠ =∠BAE ;∴AB∥CD ;
∵∠1=∠2(已知);∴∠1+∠CAE=∠2+∠CAE ;
即∠BAE=∠CAD;∴∠3=∠CAD;∴AD∥BE .
18.已知:如图,∠1=∠2,∠3=∠4.请说明DF∥BC的理由.
19.如图,GM、HN分别平分∠BGE和∠DHF,且∠1+∠2=90°,求证:AB∥CD.
20.小明在学习三角形知识时,发现如下三个有趣的结论:在Rt△ABC中,∠A=90°,BD平分∠ABC,M为直线AC上一点,ME⊥BC,垂足为E,∠AME的平分线交直线AB于点F.
(1)如图①,M为边AC上一点,则BD、MF的位置关系是 ;
如图②,M为边AC反向延长线上一点,则BD、MF的位置关系是 ;
如图③,M为边AC延长线上一点,则BD、MF的位置关系是 ;
(2)请就(1)中图①的情况写出证明过程.
21.如图1,已知三角形ABC与三角形ADE摆放在一起,点A、C、E在同一直线上,其中∠ACB=30°,∠DAE=45°,∠BAC=∠D=90°.如图2,固定三角形ABC,将三角形ADE绕点A按顺时针方向旋转,记旋转角∠CAE=α(0°<α<180°).
(1)当α为 度时,AD∥BC;
(2)在旋转过程中,试探究∠CAD与∠BAE之间的关系;
(3)当三角形ADE的一边与三角形ABC的某一边平行(不共线)时,直接写出旋转角α所有可能的度数(第(1)题的结论除外).
22.如图,直线PQ∥MN,一副三角板(∠ABC=∠CDE=90°,∠ACB=30°,∠BAC=60°,∠DCE=∠DEC=45°)按如图①放置,其中点E在直线PQ上,点B,C均在直线MN上,且CE平分∠ACN.
(1)求∠DEQ的度数;
(2)如图②,若将△ABC绕B点以每秒5°的速度按逆时针方向旋转(A,C的对应点分别为F,G).设旋转时间为t秒(0≤t≤36).
①在旋转过程中,若边BG∥CD,求t的值;
②若在△ABC绕B点旋转的同时,△CDE绕E点以每秒4°的速度按顺时针方向旋转(C,D的对应点分别为H,K).请直接写出当边BG∥HK时t的值.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
