5.1同底数幂的乘法(2)[下学期]

课件18张PPT。同底数幂的乘法你玩过魔方吗？ 魔方是匈牙利建筑师鲁比克
发明的一种智力玩具。 ★设组成魔方的每一个小立方块
（我们称它为基本单元）的棱长
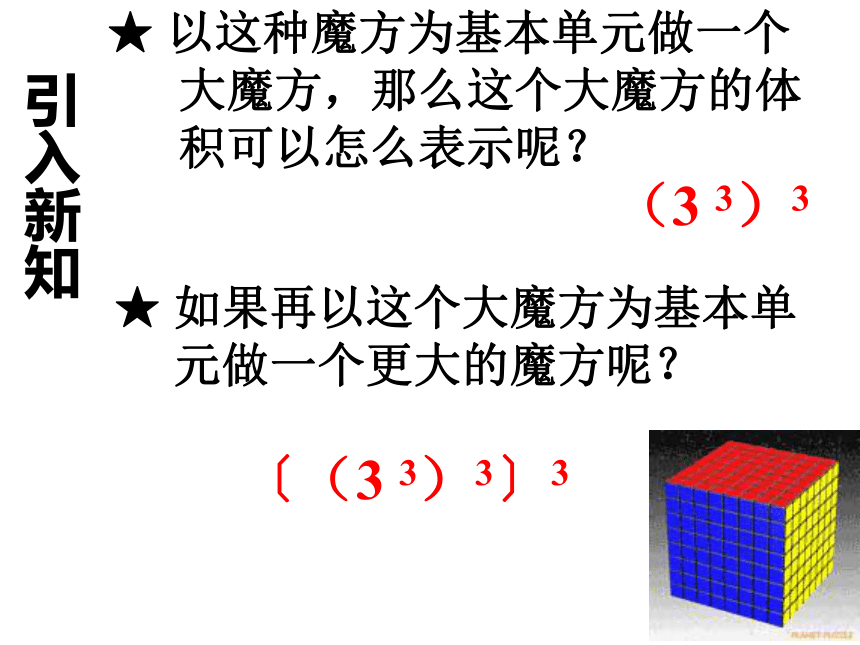
为1，那么一个魔方的体积是 。33引入新知你知道魔方的结构吗？引入新知★ 以这种魔方为基本单元做一个
大魔方，那么这个大魔方的体
积可以怎么表示呢？★ 如果再以这个大魔方为基本单
元做一个更大的魔方呢？（3 3）3〔（3 3）3〕3探究新知问题一：上述表达式是一种什么形式？（3 3）3〔（3 3）3〕3问题二：你能算出它的结果吗？幂的乘方合作学习计算下列各式，并说明理由
（1）（102）3 （2）（34）2
（3）（a3）5 （4）（am）n解（1）（102）3＝102×102×102（根据幂的意义）
＝102＋2＋2（根据同底幂相乘法则）
＝102×3
（2）（34）2＝34×34＝34＋4＝34×2=38
（3）（a3）5＝a3·a3·a3·a3·a3＝a3＋3＋3＋3＋3
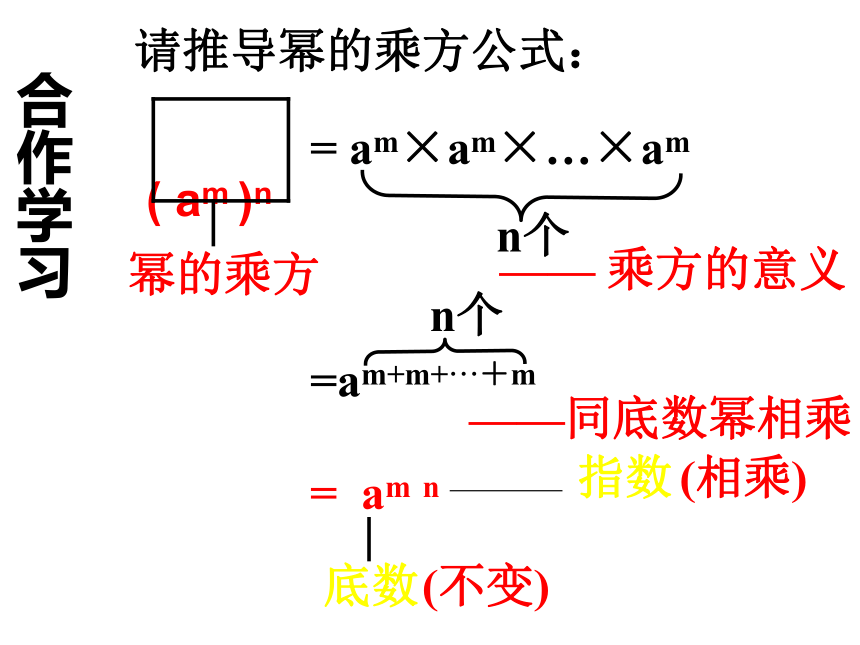
＝a3×5＝a15 ( am )n= am×am×…×am=am+m+···＋mn个n个= am n底数(不变)(相乘)合作学习请推导幂的乘方公式：—— 乘方的意义——同底数幂相乘幂的乘方法则:幂的乘方,底数不变,指数相乘( am )n = a m n 得出新知 (m.n是正整数)想一想（小组讨论） （am）n与（an）m相等吗？为什么？例1 计算
1) (107)3 2) (a4)8
3) (－5 3)3 4) 〔(－3)6〕2
5) －(y4)3 6) (a-b)3 2
解:= 10 7×3= 10212) (a4)83) (－53)34)〔(－3)6〕2= a 4×8= a 32= － 5 3×3=－5 9= 36×2= 3 121) (107)3运用新知 5) － (y4)3 =－ y4×3 =－y12(a-b)3 ×2 =(a-b)6练习：(口答)
1) (a3)4
2) a3·a4
3) ( y4)2
4) y4 · y 2
5) ( b m )2
6) b m · b 2= a7= a2m= a2+m= a12= a8= a6幂的乘方同底数幂相乘巩固新知由此你能对两个法则进行比较吗？你有什么发现？am·an= am+n
(m.n是正整数)(am)n= amn
(m.n是正整数)不变不变相加相乘同底数幂相乘与幂的乘方比较：概念比较 下面的计算对吗?如果不对 ,
应怎样改正?
(43) 5 = 4 8
（-28）3= （-2）24
(-3) 5 3 = －315
(52 )4 ×5 = 58
巩固新知（×） 415（×） －224（√） （×） 59例2 计算：解:原式=解:原式=思考题：1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672动脑筋！智能挑战 在255，344，433，522，这四个幂的数值中，
最大的一个是_______ 344幂的乘方法则：（其中m , n都是正整数）同底数幂的乘法法则：祝同学们 学习进步! 再 见