浙教版七年级下册 1.4 平行线的性质 (1)课件(共17张PPT)
文档属性
| 名称 | 浙教版七年级下册 1.4 平行线的性质 (1)课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 665.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-04-24 18:43:40 | ||
图片预览



文档简介
(共17张PPT)
1.4 平行线的性质(1)
第 1 章
平行线
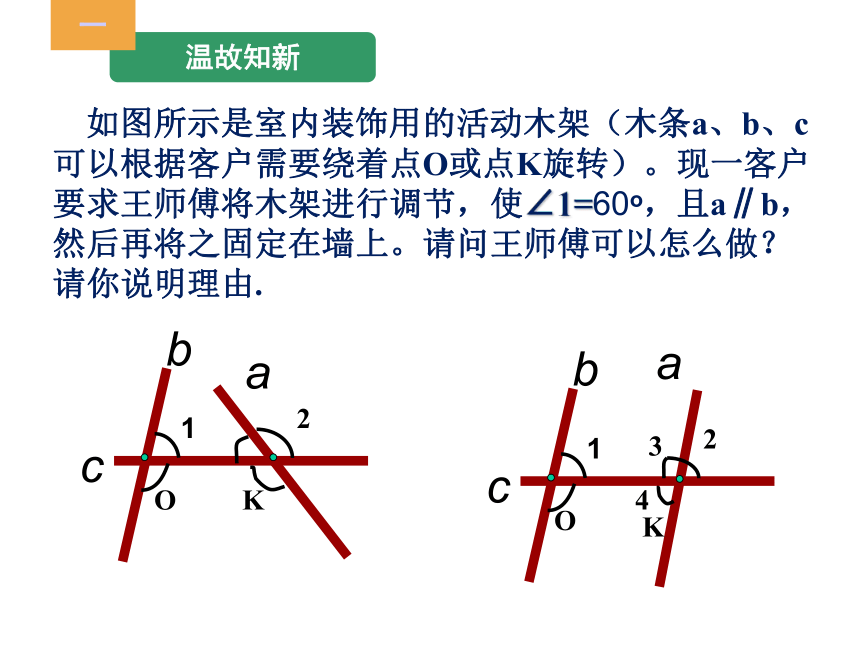
如图所示是室内装饰用的活动木架(木条a、b、c可以根据客户需要绕着点O或点K旋转)。现一客户要求王师傅将木架进行调节,使∠1=60o,且a∥b,然后再将之固定在墙上。请问王师傅可以怎么做?请你说明理由.
b
a
1
c
2
K
O
b
a
1
c
2
3
4
K
O
温故知新
一
b
a
c
K
O
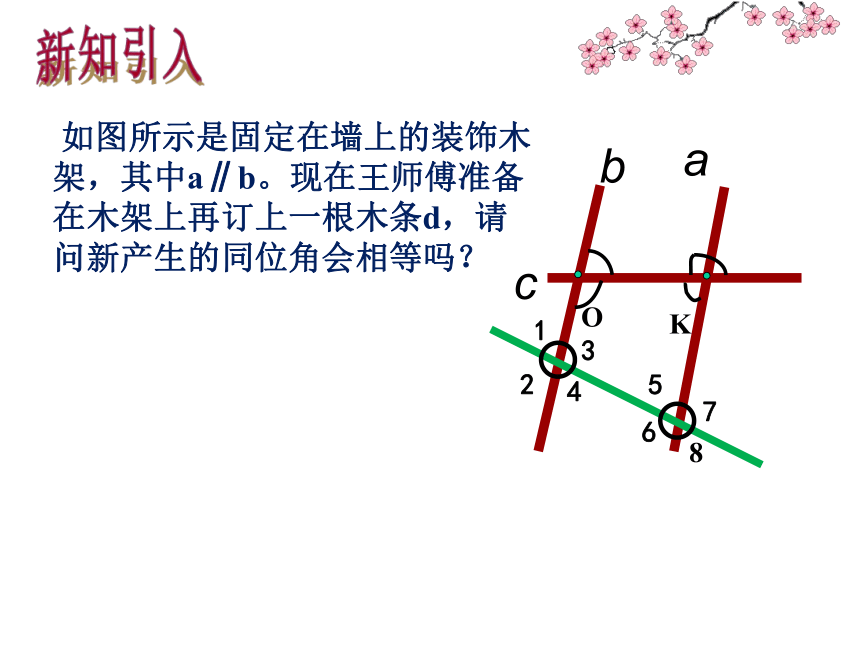
如图所示是固定在墙上的装饰木架,其中a∥b。现在王师傅准备在木架上再订上一根木条d,请问新产生的同位角会相等吗?
1
5
2
4
3
6
8
7
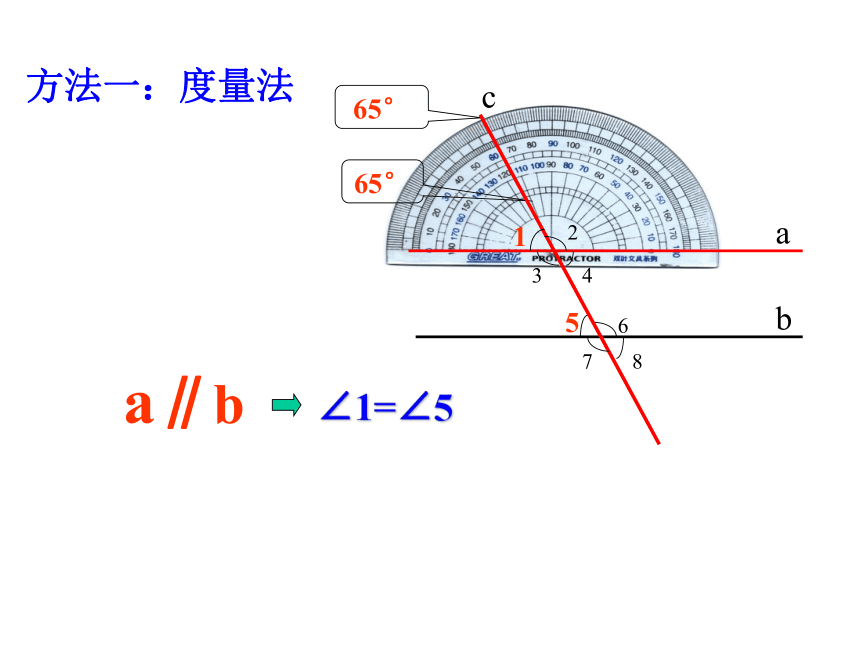
65°
65°
c
a
b
1
5
2
3
4
6
7
8
∠1=∠5
a∥b
方法一:度量法
1
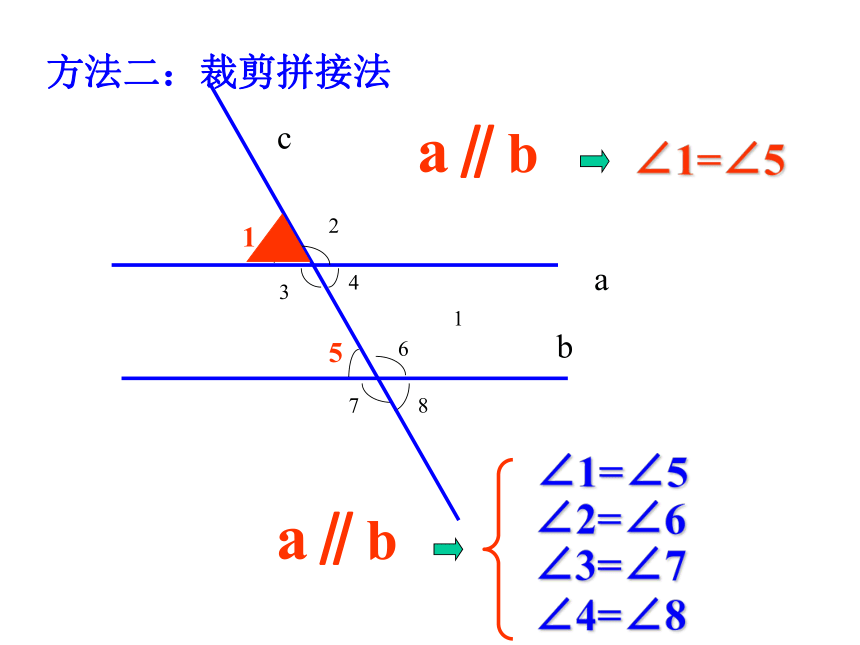
方法二:裁剪拼接法
a
c
b
5
6
8
2
3
4
7
1
∠1=∠5
a∥b
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
a∥b
c
a
b
1
5
2
3
4
6
7
8
简记为:两直线平行,同位角相等
如果两条平行直线被第三条直线所截,同位角相等
由此得到平行线的性质一:
数学语言表示:
格式一:
由已知得 a//b
根据两直线平行,同位角相等得 ∠1=∠2
格式二
∵ a//b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
c
a
b
如果直线a与b不平行,你的猜想还成立吗?
结论:如果直线a与b不平行,
同位角则不相等.
探究的反思:
(1) 同位角相等;
(2) 两条直线被第三条直线所截,同位角相等.
b
a
1
c
2
辨一辨:判断下列说法是否正确
强调:要区分清楚平行线性质1的条件和结论:
条件:两直线平行,
结论:同位角相等
辨一辨:
条件 结论 推理思路
平行线的
判定 同位角相等 两直线平行 角相等 线平行
平行线的性质 两直线平行 同位角相等 线平行 角相等
平行线的性质与判定的区别
平行线的性质与判定的共同前提:
两条直线被第三条直线所截
如图,已知直线c∥d,有下列结论:
巩固练习:
4
5
6
7
①∠1=∠7;
②∠3=∠4;
③∠5=∠6;
④ ∠2=∠6;
其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
特别强调:两直线平行,只能推出以它们为被截线的两个同位角相等, 切不可张冠李戴!建议同学们用短线加以标注确认。
C
例1 如图:梯子的各条横档互相平行,∠1=100o,求∠2的度数。
1
2
A
B
C
D
3
解:∵AB∥CD
∴∠3=∠1
∴∠2=1800-∠3=80o
(两直线平行,同位角相等)
(已知)
∵ ∠1=100o
∵ ∠3=100o
(等量代换)
(平角的意义)
∴∠2+ ∠3 =1800
(等式的基本性质)
(已知)
1
2
3
4
n
m
a
b
例2 如图,已知∠1=∠2,若直线b⊥m,则直线 a⊥m,请说明理由.
解:∵ ∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)
∴ ∠3=∠4
(两直线平行,同位角相等)
∵b⊥m(已知)
∴ ∠4=900
(垂直的意义)
∴ ∠3=900
∴a⊥m
( 等量代换 )
(垂直的定义)
练一练:
1.若∠1与∠2的是同位角,∠1=40°,则∠2等于( )
(A)40° (B)140°(C)40°或140°(D)不确定
2.已知:如图∠ADE=60°,∠B=60°,∠C=80°,
问∠ AED等于多少度?为什么
解:∵ ∠ADE=∠B=60° (已知)
∴ DE//BC( )
∴ ∠AED=∠C=80° ( )
D
两直线平行,同位角相等
同位角相等,两直线平行
3.已知:直线AB和直线CD被直线EF所截,交点分别为G和M,且AB ∥CD,若GH是∠EGB的平分线,MN是∠EMD的平分线,则GH和直线MN是否平行?为什么?
如图所示,AB∥CD,点M是平面上的一点,
(1)如图1所示,若∠MAB=35°,∠MCD=75°,
求∠AMC的度数.
(2)如图2和图3所示,若∠MAB=x°,∠MCD=y°,
分别求出∠ AMC的度数(用含x、y代数式表示).
拓展提升
M
M
图1
图2
图3
感悟提升
七
思
想
方
法
建模思想
转化思想
分类思想
解
题
策
略
由因导果
执果索因
两头凑
知
识
平行线的性质1
分层作业
A层(成绩一般的同学):完成课本1.4(1)后面的作业题。
B层(学有余力的同学):1.完成课本1.4(1)后面的作业题;
2.完成下列两个选做题
1.如图,将一张长方形纸片沿EF折叠后,使得点A、B分别落在点A、B的位置,如果∠2=56°,那么∠1=( )
2.如图,已知AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,猜想∠BDE与∠C有怎样的大小关系?并说明理由.
1.4 平行线的性质(1)
第 1 章
平行线
如图所示是室内装饰用的活动木架(木条a、b、c可以根据客户需要绕着点O或点K旋转)。现一客户要求王师傅将木架进行调节,使∠1=60o,且a∥b,然后再将之固定在墙上。请问王师傅可以怎么做?请你说明理由.
b
a
1
c
2
K
O
b
a
1
c
2
3
4
K
O
温故知新
一
b
a
c
K
O
如图所示是固定在墙上的装饰木架,其中a∥b。现在王师傅准备在木架上再订上一根木条d,请问新产生的同位角会相等吗?
1
5
2
4
3
6
8
7
65°
65°
c
a
b
1
5
2
3
4
6
7
8
∠1=∠5
a∥b
方法一:度量法
1
方法二:裁剪拼接法
a
c
b
5
6
8
2
3
4
7
1
∠1=∠5
a∥b
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
a∥b
c
a
b
1
5
2
3
4
6
7
8
简记为:两直线平行,同位角相等
如果两条平行直线被第三条直线所截,同位角相等
由此得到平行线的性质一:
数学语言表示:
格式一:
由已知得 a//b
根据两直线平行,同位角相等得 ∠1=∠2
格式二
∵ a//b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
c
a
b
如果直线a与b不平行,你的猜想还成立吗?
结论:如果直线a与b不平行,
同位角则不相等.
探究的反思:
(1) 同位角相等;
(2) 两条直线被第三条直线所截,同位角相等.
b
a
1
c
2
辨一辨:判断下列说法是否正确
强调:要区分清楚平行线性质1的条件和结论:
条件:两直线平行,
结论:同位角相等
辨一辨:
条件 结论 推理思路
平行线的
判定 同位角相等 两直线平行 角相等 线平行
平行线的性质 两直线平行 同位角相等 线平行 角相等
平行线的性质与判定的区别
平行线的性质与判定的共同前提:
两条直线被第三条直线所截
如图,已知直线c∥d,有下列结论:
巩固练习:
4
5
6
7
①∠1=∠7;
②∠3=∠4;
③∠5=∠6;
④ ∠2=∠6;
其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
特别强调:两直线平行,只能推出以它们为被截线的两个同位角相等, 切不可张冠李戴!建议同学们用短线加以标注确认。
C
例1 如图:梯子的各条横档互相平行,∠1=100o,求∠2的度数。
1
2
A
B
C
D
3
解:∵AB∥CD
∴∠3=∠1
∴∠2=1800-∠3=80o
(两直线平行,同位角相等)
(已知)
∵ ∠1=100o
∵ ∠3=100o
(等量代换)
(平角的意义)
∴∠2+ ∠3 =1800
(等式的基本性质)
(已知)
1
2
3
4
n
m
a
b
例2 如图,已知∠1=∠2,若直线b⊥m,则直线 a⊥m,请说明理由.
解:∵ ∠1=∠2(已知)
∴a∥b
(同位角相等,两直线平行)
∴ ∠3=∠4
(两直线平行,同位角相等)
∵b⊥m(已知)
∴ ∠4=900
(垂直的意义)
∴ ∠3=900
∴a⊥m
( 等量代换 )
(垂直的定义)
练一练:
1.若∠1与∠2的是同位角,∠1=40°,则∠2等于( )
(A)40° (B)140°(C)40°或140°(D)不确定
2.已知:如图∠ADE=60°,∠B=60°,∠C=80°,
问∠ AED等于多少度?为什么
解:∵ ∠ADE=∠B=60° (已知)
∴ DE//BC( )
∴ ∠AED=∠C=80° ( )
D
两直线平行,同位角相等
同位角相等,两直线平行
3.已知:直线AB和直线CD被直线EF所截,交点分别为G和M,且AB ∥CD,若GH是∠EGB的平分线,MN是∠EMD的平分线,则GH和直线MN是否平行?为什么?
如图所示,AB∥CD,点M是平面上的一点,
(1)如图1所示,若∠MAB=35°,∠MCD=75°,
求∠AMC的度数.
(2)如图2和图3所示,若∠MAB=x°,∠MCD=y°,
分别求出∠ AMC的度数(用含x、y代数式表示).
拓展提升
M
M
图1
图2
图3
感悟提升
七
思
想
方
法
建模思想
转化思想
分类思想
解
题
策
略
由因导果
执果索因
两头凑
知
识
平行线的性质1
分层作业
A层(成绩一般的同学):完成课本1.4(1)后面的作业题。
B层(学有余力的同学):1.完成课本1.4(1)后面的作业题;
2.完成下列两个选做题
1.如图,将一张长方形纸片沿EF折叠后,使得点A、B分别落在点A、B的位置,如果∠2=56°,那么∠1=( )
2.如图,已知AD⊥BC,FG⊥BC,垂足分别为D、G,且∠1=∠2,猜想∠BDE与∠C有怎样的大小关系?并说明理由.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
