第1章 平行线 练习题(含解析) 2021-2022学年浙江省各地浙教版数学七年级下册期末试题选编
文档属性
| 名称 | 第1章 平行线 练习题(含解析) 2021-2022学年浙江省各地浙教版数学七年级下册期末试题选编 |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-02 20:47:45 | ||
图片预览

文档简介
第1章 平行线
一、单选题
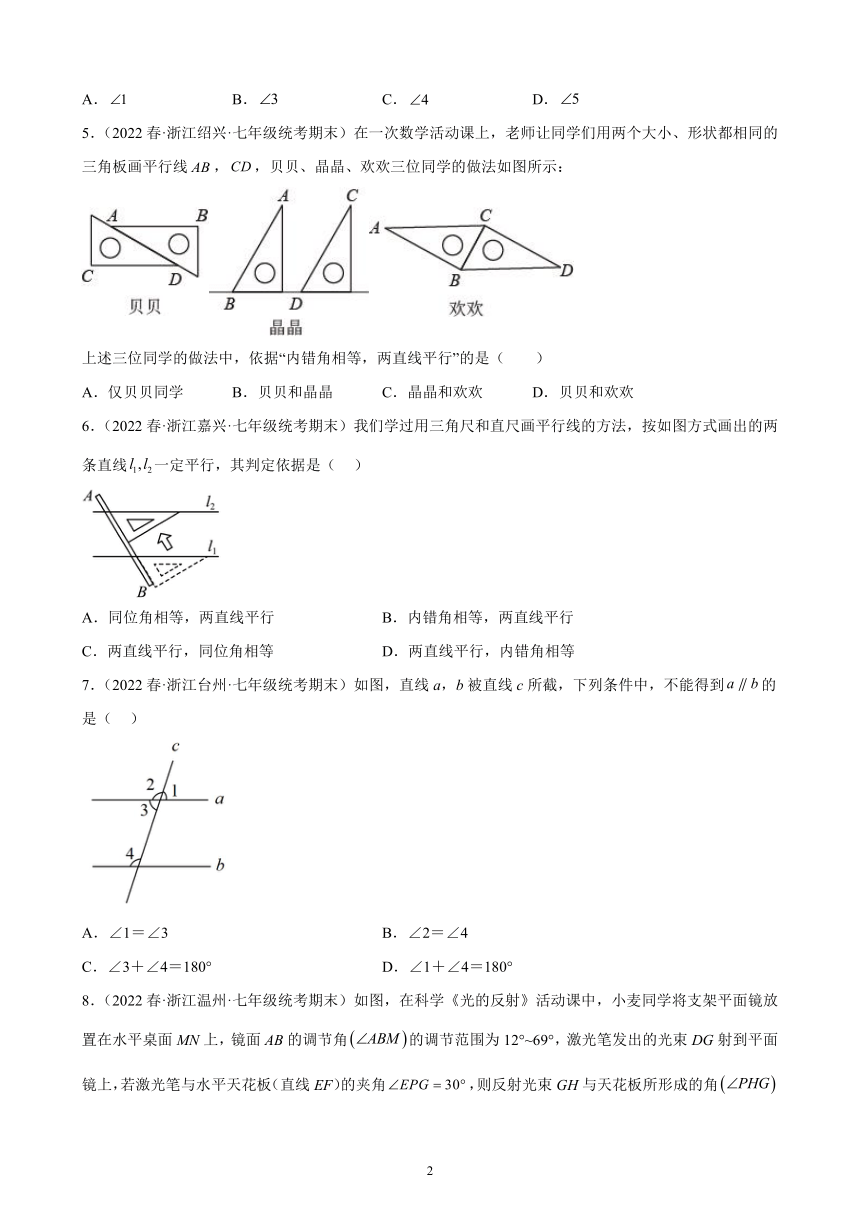
1.(2022春·浙江绍兴·七年级统考期末)据说中国最早的风筝是由古代哲学家墨翟制作的.如图风筝的骨架构成了多种位置关系的角.下列角中与∠1构成同位角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.(2022春·浙江湖州·七年级统考期末)如图,∠1和∠2是内错角的是( )
A. B.C. D.
3.(2022春·浙江杭州·七年级统考期末)如图,说法正确的是( )
A.和是内错角 B.和是内错角
C.和是同位角 D.和是同旁内角
4.(2022春·浙江台州·七年级统考期末)在铺设铁轨时,两条直轨必须是互相平行的,如图,已经知道是直角,那么再度量图中已标出的哪个角,不能判断两条直轨是否平行( )
A. B. C. D.
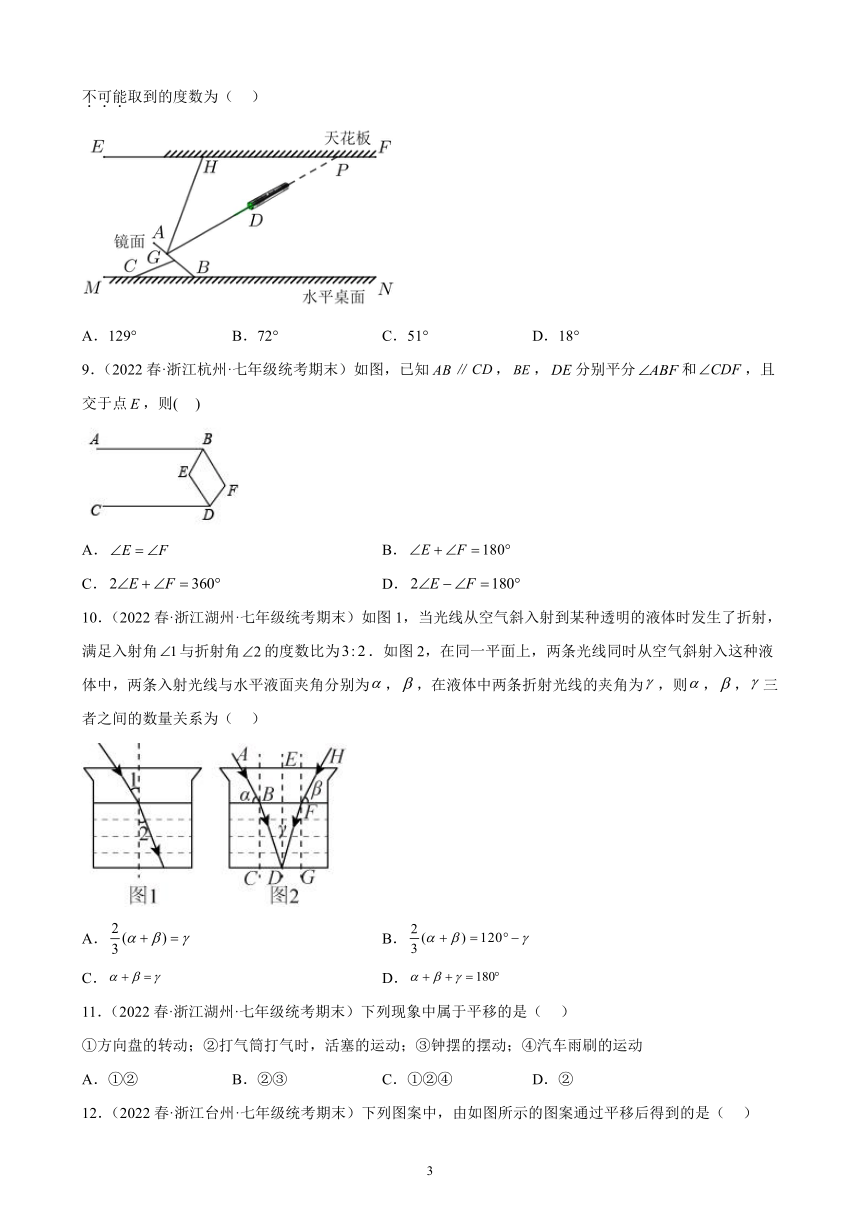
5.(2022春·浙江绍兴·七年级统考期末)在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线,,贝贝、晶晶、欢欢三位同学的做法如图所示:
上述三位同学的做法中,依据“内错角相等,两直线平行”的是( )
A.仅贝贝同学 B.贝贝和晶晶 C.晶晶和欢欢 D.贝贝和欢欢
6.(2022春·浙江嘉兴·七年级统考期末)我们学过用三角尺和直尺画平行线的方法,按如图方式画出的两条直线一定平行,其判定依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.两直线平行,同位角相等 D.两直线平行,内错角相等
7.(2022春·浙江台州·七年级统考期末)如图,直线a,b被直线c所截,下列条件中,不能得到的是( )
A.∠1=∠3 B.∠2=∠4
C.∠3+∠4=180° D.∠1+∠4=180°
8.(2022春·浙江温州·七年级统考期末)如图,在科学《光的反射》活动课中,小麦同学将支架平面镜放置在水平桌面MN上,镜面AB的调节角的调节范围为12°~69°,激光笔发出的光束DG射到平面镜上,若激光笔与水平天花板(直线EF)的夹角,则反射光束GH与天花板所形成的角不可能取到的度数为( )
A.129° B.72° C.51° D.18°
9.(2022春·浙江杭州·七年级统考期末)如图,已知∥,,分别平分和,且交于点,则( )
A. B.
C. D.
10.(2022春·浙江湖州·七年级统考期末)如图1,当光线从空气斜入射到某种透明的液体时发生了折射,满足入射角与折射角的度数比为.如图2,在同一平面上,两条光线同时从空气斜射入这种液体中,两条入射光线与水平液面夹角分别为,,在液体中两条折射光线的夹角为,则,,三者之间的数量关系为( )
A. B.
C. D.
11.(2022春·浙江湖州·七年级统考期末)下列现象中属于平移的是( )
①方向盘的转动;②打气筒打气时,活塞的运动;③钟摆的摆动;④汽车雨刷的运动
A.①② B.②③ C.①②④ D.②
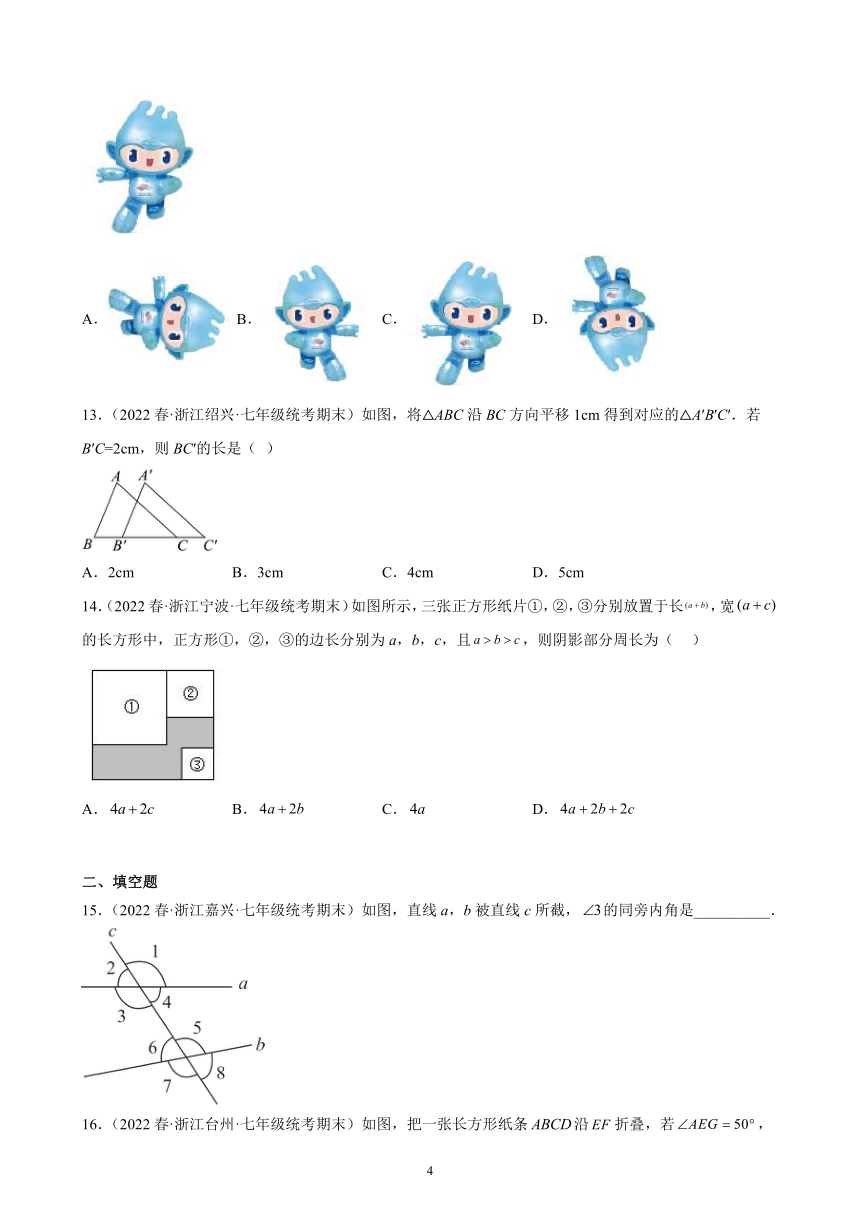
12.(2022春·浙江台州·七年级统考期末)下列图案中,由如图所示的图案通过平移后得到的是( )
A.B. C. D.
13.(2022春·浙江绍兴·七年级统考期末)如图,将△ABC沿BC方向平移1cm得到对应的△A′B′C′.若B′C=2cm,则BC′的长是( )
A.2cm B.3cm C.4cm D.5cm
14.(2022春·浙江宁波·七年级统考期末)如图所示,三张正方形纸片①,②,③分别放置于长,宽的长方形中,正方形①,②,③的边长分别为a,b,c,且,则阴影部分周长为( )
A. B. C. D.
二、填空题
15.(2022春·浙江嘉兴·七年级统考期末)如图,直线a,b被直线c所截,的同旁内角是__________.
16.(2022春·浙江台州·七年级统考期末)如图,把一张长方形纸条沿折叠,若,则______°.
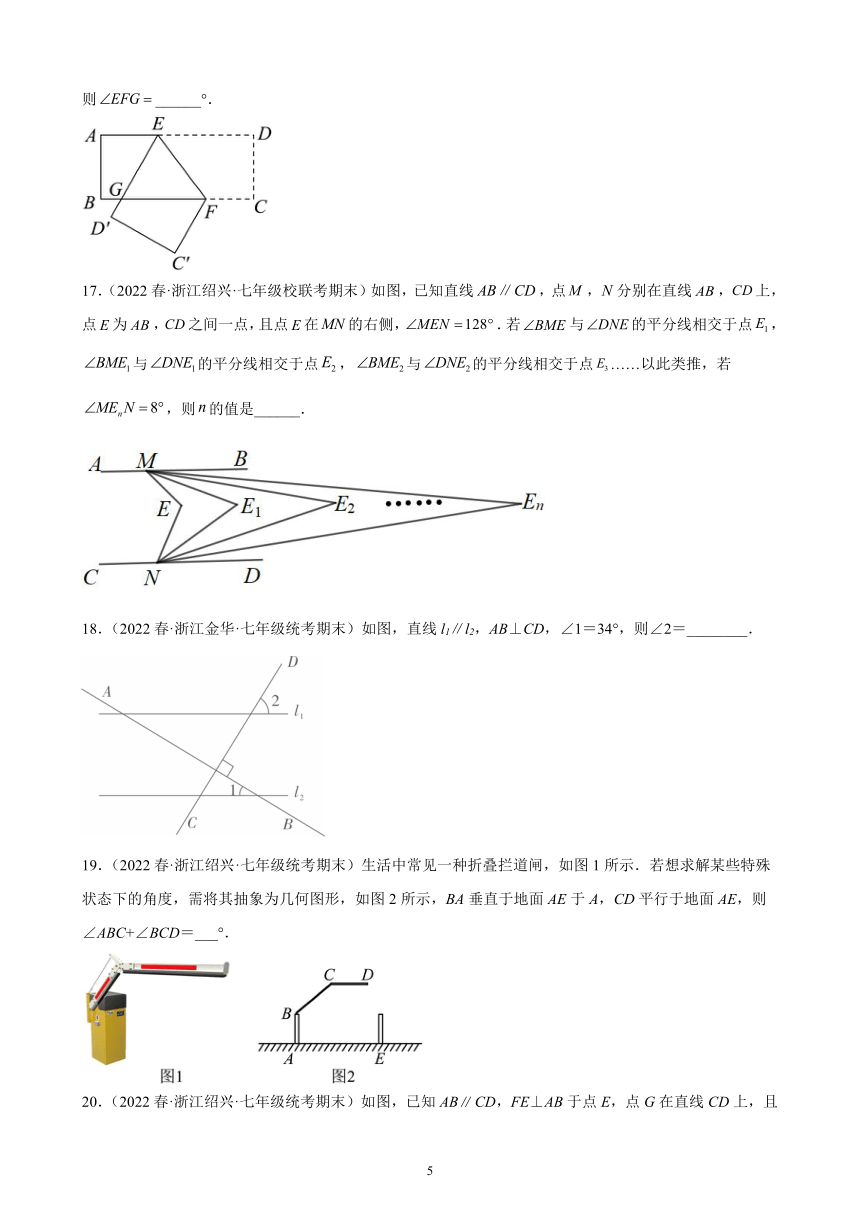
17.(2022春·浙江绍兴·七年级校联考期末)如图,已知直线,点,分别在直线,上,点为,之间一点,且点在的右侧,.若与的平分线相交于点,与的平分线相交于点,与的平分线相交于点……以此类推,若,则的值是______.
18.(2022春·浙江金华·七年级统考期末)如图,直线l1∥l2,AB⊥CD,∠1=34°,则∠2=________.
19.(2022春·浙江绍兴·七年级统考期末)生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD=___°.
20.(2022春·浙江绍兴·七年级统考期末)如图,已知ABCD,FE⊥AB于点E,点G在直线CD上,且位于直线EF的右侧.
(1)若∠EFG=120°,则∠FGC的度数是 _____;
(2)若∠AEH=∠FGH=20°,∠H=50°,则∠EFG的度数是 _____.
三、解答题
21.(2022春·浙江湖州·七年级统考期末)长江汛期即将来临,为了便于夜间查看江水及两岸河堤的情况,防汛指挥部在一危险地带两岸各安置了一探照灯(如图1),假定这一带长江两岸河堤是平行的,即,连结,且.灯射线自顺时针旋转至便立即回转,灯射线自顺时针旋转至便立即回转,两灯不停交叉照射巡视.若灯转动的速度是1度/秒,灯转动的速度是3度/秒.
(1)若两灯同时转动,在灯射线第一次转到之前,两灯射出的光线交于点.
①如图1,当两灯光线同时转动50秒时,求的度数.
②如图2,过作交于点,则在转动过程中,求与的比值,并说明理由.
(2)若灯射线先转动30秒,灯射线才开始转动,在灯射线第一次转到之前,灯转动几秒,两灯的光线互相平行?
22.(2022春·浙江衢州·七年级统考期末)已知△ABC与△ADE共顶点A,,顶点B和C在直线上(点B在点C的左侧),顶点D和E在直线上(点D在点E的左侧),且直线.
(1)如图1,顶点A在与之间,判断∠BAD与是否相等,并说明理由.
(2)如图2,顶点A在与之间,∠ABC的外角平分线与∠AED的角平分线交于点F,若,求∠BFE的度数.
(3)若顶点A在直线的下方,且顶点B、A、D不在一条直线上,∠ABC的外角平分线与∠AED的角平分线交于点F,记,,请探究与的数量关系,并直接写出结论.
23.(2022春·浙江台州·七年级统考期末)如图,已知:,.求证:.
证明:∵(已知),
∴____________(________________________).
∴(_____________________________).
∵(已知),
∴(等量代换).
∴____________(__________________________).
∴(______________________________).
24.(2022春·浙江宁波·七年级统考期末)如图,在中,点分别在上,且, .
(1)求证: ;
(2)若平分,,求的度数.
25.(2022春·浙江金华·七年级统考期末)如图是单位长度为1的网格,△ABC的三个顶点都在格点上,点M也在格点上.只用无刻度直尺在网格内按要求完成作图并回答问题:
(1)过点M作平行于BC的直线l.
(2)将图中△ABC先向左平移2个单位,再向上平移1个单位得到.
①作出平移后的;
②点P是三角形ABC内任意一点,则平移过程中P点经过的路径长为 .
26.(2022春·浙江台州·七年级统考期末)如图,在7×5的方格中,三角形ABC的顶点均在格点上,点D为格点.
(1)在图中作出线段DE(E点在格上),使;
(2)在图中作出线段DF(F点在格上),使.
参考答案:
1.A
【分析】根据同位角的定义解答.两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
【详解】解:由图可得,与构成同位角的是.
故选:A.
【点睛】本题主要考查了同位角的定义,解题的关键是明确同位角的边构成“”形,内错角的边构成“”形,同旁内角的边构成“”形.
2.A
【分析】根据内错角的定义:两个角位于截线两侧,且在两条被截线之间的一对角,逐一判断即可.
【详解】解:A图中,∠1与∠2是内错角,符合题意;
B图中,∠1与∠2不在两条被截线之间,不是内错角,不符合题意;
C图中,∠1与∠2是同旁内角,不符合题意;
D图中,∠1与∠2是同位角,不符合题意;
故选:A.
【点睛】本题考查了同位角、内错角、同旁内角的定义,掌握各自的位置关系是解题关键.
3.B
【分析】根据同位角,内错角,同旁内角的定义,逐项判断即可求解.
【详解】解:A、和是同位角,故本选项错误,不符合题意;
B、和是内错角,故本选项正确,符合题意;
C、和是内错角,故本选项错误,不符合题意;
D、和不是同旁内角,故本选项错误,不符合题意;
故选:B
【点睛】本题主要考查了同位角,内错角,同旁内角的定义,熟练掌握两条直线被第三条直线所截,在截线的同旁、被截两直线的同一方,我们把这种位置关系的角称为同位角;两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角;两条直线被第三条直线所截,在两条被截线之间,并在截线同旁的两个角称为同旁内角是解题的关键.
4.A
【分析】因为∠2是直角,只要找出与∠2互为同位角、内错角、同旁内角的其他角,根据平行线的判定定理判定即可得到正确答案.
【详解】因为∠2是直角,∠4和∠2是同位角,如果度量出,
根据“同位角相等,两直线平行”,就可以判断两条直轨平行,
∠5和∠2是内错角,如果度量出,
根据“内错角相等,两直线平行”,就可以判断两条直轨平行,
∠3和∠2是同旁内角,如果度量出,
根据“同旁内角互补,两直线平行”,就可以判断两条直轨平行,
所以答案为:A.
【点睛】本题考查两直线平行的判定定理,解决本题的关键是熟练的掌握平行线的判定定理.
5.D
【分析】根据平行线的判定定理进行判断,即可得到答案.
【详解】解:根据题意,
贝贝:利用内错角相等,两直线平行;
晶晶:利用同位角相等,两直线平行;
欢欢:利用内错角相等,两直线平行;
故选:D.
【点睛】本题考查了平行线的判定与性质.属于基础题,熟记平行线的判定定理即可填空.
6.A
【分析】根据同位角相等,两直线平行,即可求解.
【详解】解:根据题意得:两条直线一定平行,其判定依据是同位角相等,两直线平行.
故选:A
【点睛】本题主要考查了平行线的判定,熟练掌握同位角相等,两直线平行是解题的关键.
7.A
【分析】根据平行线的判定定理判断求解即可.
【详解】解:A.由∠1=∠3,不能判定a∥b,故选项符合题意;
B.∵∠2=∠4,
∴a∥b,
故选项不符合题意;
C.∵∠3+∠4=180°,
∴a∥b,
故选项不符合题意;
D.∵∠1+∠4=180°,∠1=∠3,
∴∠3+∠4=180°,
∴a∥b,
故选项不符合题意;
故选:A.
【点睛】此题考查了平行线的判定,熟记平行线的判定定理是解题的关键.
8.C
【分析】分当时,如图1所示,当时,如图2所示,两种情况,利用平行线的性质求解即可.
【详解】解:当时,如图1所示,过点G作,
∵,
∴,
∴∠PGQ =∠EPG=30°,∠BGQ=∠ABM,
∴∠PGB=∠PGQ+∠BGQ=30°+∠ABM,
由反射定理可知,∠AGH=∠PGB=30°+∠ABM,
∴∠PGH=180°-∠AGH-∠PGB=120°-2∠ABM,
∴∠HGQ=∠PGH+∠PGQ=150°-2∠ABM,
∴∠PHG=180°-∠HGQ=30°+2∠ABM,
∴
当时,如图2所示,过点G作,
同理可得∠PGQ=∠EPG=30°,∠BGQ=∠ABM,∠PHG=∠HGQ,
∴∠AGP=∠HGB=∠HGQ+∠QGB=∠PHG+∠ABM,
∴∠PGH=180°-∠AGP-∠HGB=180°-2∠PHG-2∠ABM,
∴∠HGP=∠PGQ-∠PGH=2∠PHG+2∠ABM-150°,
∴∠PHG=150°-2∠ABM,
∴,
综上所述,或,
故选C.
【点睛】本题主要考查了平行线的性质,正确作出辅助线和利用分类讨论的思想求解是解题的关键.
9.C
【分析】过点作,利用平行线的性质可证得,可以得到与的关系
【详解】解:过点作,如图:
,
∴CD∥EM ,
∴
∵的平分线与的平分线相交于点,
∴,
∴,
∵,
∴
∴
整理得:.
故选:C.
【点睛】本题主要考查了平行线的性质和角平分线,解决问题的关键是作辅助线构造同旁内角以及内错角,依据平行线的性质进行推导计算,解题时注意数形结合思想的运用.
10.B
【分析】过点B、D、F分别作水平线的垂线,则,根据平行线的性质与光的折射原理即可得到答案
【详解】如图:过点B、D、F分别作水平线的垂线,则
由题知
即:
即
故选B
【点睛】本题考查了平行线的性质,光学原理,读懂题并熟练掌握平行线的性质是关键.
11.D
【分析】直接根据平移的定义分别判断.
【详解】解:①方向盘的转动是旋转,故不符合题意;
②打气筒打气时,活塞的运动是平移,故符合题意;
③钟摆的摆动是旋转,故不符合题意;
④汽车雨刷的运动是旋转,故不符合题意;
综上分析可知,属于平移的是②,故D正确.
故选:D.
【点睛】本题考查了生活中的平移现象,熟练掌握平移的定义是解答本题的关键. 平移是指在平面内,将一个图形上的所有点都按照某个方向作相同距离的移动.平移不改变图形的形状和大小,只是改变位置.
12.C
【分析】根据图形平移的性质对各选项进行逐一分析即可.
【详解】解:A.由图中所示的图案通过旋转而成,故A错误,不符合题意;
B.由图中所示的图案与原图案成轴对称,不能通过平移得到,故B错误,不符合题意;
C.由图中所示的图案通过平移而成,故C正确,符合题意;
D.由图中所示的图案通过翻折而成,故D错误,不符合题意.
故选:C.
【点睛】本题主要考查了平移的性质,熟练掌握平移前后图形的形状大小不变,只是改变了位置是解题的关键.
13.C
【分析】据平移的性质可得BB′=CC′=1,列式计算即可得解.
【详解】解:∵△ABC沿BC方向平移1cm得到△A′B′C′,
∴BB′=CC′=1cm,
∵B′C=2cm,
∴BC′= BB′+ B′C+CC′=1+2+1=4(cm).
故选:C.
【点睛】本题考查了平移的性质,熟记性质得到相等的线段是解题的关键.
14.A
【分析】根据平移的性质求出水平边之和及竖直边之和,再列式计算解答.
【详解】解:将阴影部分水平的边通过平移可得水平边之和为:2(a+b),
将阴影部分竖直的边通过平移可得竖直边之和为:2(a+c-b),
∴阴影部分的周长为:2(a+b)+2(a+c b)=2a+2b+2a+2c 2b=4a+2c,
故选:A.
【点睛】此题主要考查了平移的性质,整式的加减,根据平移的性质求出水平边之和及竖直边之和是解题的关键.
15.∠6
【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,这样的一对角叫做同旁内角.
【详解】解:∵直线a、b被直线c所截,
∴∠3的同旁内角是∠6.
故答案为:∠6.
【点睛】本题主要考查了同旁内角的概念,三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定,同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.
16.65
【分析】先根据已知条件和邻补角的性质得∠DEG=130°,再由折叠的性质得到∠DEF=∠FEG=∠DEG,再根据平行线的性质得到∠DEF=65°即可.
【详解】解:∵∠AEG=50°,
∴∠DEG=180°-50°=130°,
∵把一张长方形纸片ABCD沿EF折叠,
∴∠DEF=∠FEG=∠DEG=65°,
∵四边形ABCD是长方形,
∴ADBC,
∴∠DEF=65°.
故答案为:65.
【点睛】此题考查了折叠的性质以及平行线的性质,解题的关键是熟练掌握折叠与平行线的性质,找到相等的角.
17.4
【分析】作EF//AB则AB//CD//EF,根据平行线的性质得出∠MEN=∠BME+∠DME=128°,同理∠ME1N=(∠BME+∠DME) =64°,∠ME2N=(∠BME1+∠DME1) =32°,可归纳规律∠ME=(∠BME-1+∠DME-1) =,依此建立方程=8°求解即可解答.
【详解】解:如图:作EF//AB
∵AB//CD
∴AB//CD//EF
∴∠FEM=∠BME, ∠FEN=∠DNE,
∴∠MEN=∠BME+∠DME=∠FEM +∠FEN =∠MEN= 128°
同理:ME1N=(∠BME+∠DME) =64°,
∠ME2N=(∠BME1+∠DME1) =32°
…
∠ME=(∠BME-1+∠DME-1) =
由题意得:=8°,解得n=4.
故答案为4.
【点睛】本题考查了平行线的性质、探索图形规律、角平分线的定义等知识点,正确的识别图形、归纳图形规律是解答本题的关键.
18.56°/56度
【分析】由可得,由可得.
【详解】解:,
,
又,
,
,
.
故答案为:.
【点睛】本题考查了平行线的性质、垂直的定义,熟练掌握相关性质定理是解题的关键.
19.270
【分析】过点B作BF∥AE,从而得到CD∥AE∥BF,根据平行线的性质得到∠BCD+∠CBF=180°,∠ABF=90°,即可得到结论.
【详解】如图,过点B作BF∥AE,
∵CD∥AE,
∴CD∥AE∥BF,
∴∠BCD+∠CBF=180°,∠ABF+∠BAE=180°,
∵AB⊥AE,
∴∠BAE=90°,
∴∠ABF=90°,
∴∠ABC+∠BCD=∠ABF+∠CBF+∠BCD= 90°+180°=270°.
故答案为:270.
【点睛】本题主要考查了平行线的判定与性质,正确作出辅助线,熟记平行线的性质是解题的关键.
20. 30°/30度 140°/140度
【分析】(1)过点F作FM∥AB,根据平行线的性质求解即可;
(2)过点F作FM∥AB,过点H作HN∥AB,根据平行线的性质求解即可.
【详解】解:(1)过点F作FM∥AB,
∵FE⊥AB,FM∥AB,
∴FE⊥FM,
∴∠EFM=90°,
∵∠EFG=120°,
∴∠MFG=∠EFG∠EFM=30°,
∵FM∥AB,AB∥CD,
∴FM∥CD,
∴∠FGC=∠MFG=30°,
故答案为:30°;
(2)过点F作FM∥AB,过点H作HN∥AB,
∴∠AEH=∠EHN=20°,
∵∠EHG=50°,
∴∠NHG=∠EHG-∠EHN=30°,
∵HN∥AB,AB∥CD,
∴HN∥CD,
∴∠CGH=∠NHG=30°,
∵∠FGH=20°,
∴∠FGC=∠CGH+∠FGN=50°,
根据(1)知,∠EFM=90°,∠FGC=∠MFG,
∴∠MFG=50°,
∴∠EFG=∠EFM+∠MFG=140°,
故答案为:140°.
【点睛】此题考查了平行线的性质,熟记平行线的性质定理是解题的关键.
21.(1)①;②比值为,详见解析
(2)灯转动15秒或82.5秒时,两灯的光束互相平行
【分析】(1)①当转动50秒时,有,即有,根据,即可得解;②过点作,得到,,即有,,根据,可得,再根据,可得,即问题得解;
(2)设A灯转动秒,两灯的光束互相平行,A灯先转动30秒,则AQ转到AP还需要180-30=150(秒)即,①当B射线第一次垂直MN时,用时90÷3=30(秒),此时A射线共计运动30+30=60秒,即,即在灯射线到达之前,先证明,即有:,即可求解;②在灯射线到达之后,回到前,根据①中,同理有:,即有:,即可求解;③在灯射线回到后,第二次到前,由题意得:,即可求解,即问题得解.
【详解】(1)两灯速度为:灯A转动的速度是1度/秒,灯B转动的速度是3度/秒.
①当转动50秒时,,
∴,
∴,
故答案为:15°;
②比值为:,理由如下,
如图2,过点作,
∵,
∴,
设两灯转动时间为秒,则,,
∴,,
∴,
即,
又∵,
即,
而,
∴
.
∴.
即比值为:;
(2)两灯速度为:灯A转动的速度是1度/秒,灯B转动的速度是3度/秒.
设A灯转动秒,两灯的光束互相平行,
A灯先转动30秒,则AQ转到AP还需要180-30=150(秒)
即,
①当B射线第一次垂直MN时,用时90÷3=30(秒),
此时A射线共计运动30+30=60秒,即,
即在灯射线到达之前,如图3所示,
∵,,
∴,,
∴,
∴,
即有:,
解得:(秒);
②如图4,在灯射线到达之后,回到前,
根据①中,同理有:
∵
即有:,
解得:.
③如图5,在灯射线回到后,第二次到前,
由题意得:
,解得:(舍去).
综上所述,灯转动15秒或82.5秒时,两灯的光束互相平行.
【点睛】本题主要考查了平行线的性质以及角的和差关系,厘清角度之间的关系并注意分类讨论是解答本题的关键.
22.(1),理由见解析
(2)100°
(3)或
【分析】(1)过点A作,根据平行线的性质直接求解即可得到结论;
(2)根据(1)中的方法可知,,根据角平分线的性质及邻补角的定义等量代换即可得到结论;
(3)令,根据角平分线定义得,,过作,过作,得到,从而根据点与的关系分五种情况求解,由角度和差关系得到,或,联立方程组得到或者.
【详解】(1)解:.
过点A作,如图所示:
,
∴,
∴,
,
∴,
∴;
(2)解:如图所示:
由(1)可知,
同(1)理可得,
∵BF平分∠ABH,EF平分∠AED,
∴,
∵,
∴,,
;
(3)解:根据点与的关系分五种情况求解:
1..点在的边左侧,如图所示:
令,则根据角平分线定义得,,
过作,过作,则,
,,
①,
在中,,
,
,
②,
由①得,
由②得,
将①代入②得;
2.点在的边上,如图所示:
令,则根据角平分线定义得,,
过作,过作,则,
,,
①,
在中,,
,
,
②,
由①得,
由②得,
将①代入②得;
3.点在内,如图所示:
令,则根据角平分线定义得,,
过作,过作,则,
,,
①,
在中,,
,
,
②,
由①得,
由②得,
将①代入②得;
4.点在的边上,,如图所示:
令,则根据角平分线定义得,,
过作,过作,则,
,,
①,
在中,,
,
,
②,
由①得,
由②得,
将①代入②得,
,,满足;
5.点在的边右侧,如图所示:
令,则根据角平分线定义得,,
过作,过作,则,
,,
①,
在中,,
,
,
②,
由①得,
由②得,
将①代入②得;
综合上述1、2、3、4、5可得或.
【点睛】本题考查平行线的性质,涉及到角平分线的性质、邻补角定义、直角三角形锐角互余等性质,根据题意作出辅助线,分类讨论并根据图形恰当表示出各角之间的关系是解决问题的关键.
23.DE;AF;同位角相等,两直线平行;两直线平行,同位角相等;AB;CD;内错角相等,两直线平行;两直线平行,内错角相等
【分析】先通过已知条件证明DEAF,再由两直线平行同位角相等和等量代换证出ABCD,再根据两直线平行,内错角相等得出.
【详解】证明:∵(已知),
∴DEAF(同位角相等,两直线平行).
∴(两直线平行,同位角相等).
∵(已知),
∴(等量代换).
∴ABCD(内错角相等,两直线平行).
∴(两直线平行,内错角相等).
故答案为:DE;AF;同位角相等,两直线平行;两直线平行,同位角相等;AB;CD;内错角相等,两直线平行;两直线平行,内错角相等.
【点睛】本题考查平行线的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.
24.(1)见解析
(2)
【分析】(1)根据平行线的性质得出∠1=∠C,求出∠2=∠C,再根据平行线的判定得出即可;
(2)根据平行线的性质得出∠B+∠BAF=180°,求出∠BAF,根据角平分线的定义救出∠2,再求出∠1即可.
【详解】(1)∵DEAC,
∴∠1=∠C,
∵∠1=∠2,
∴∠2=∠C,
∴AFBC;
(2)∵AFBC,
∴∠B+∠BAF=180°,
∵∠B=48°,
∴∠BAF=180°-48°=132°,
∵AC 平分∠BAF,
∴∠2=∠BAF=66°,
∵∠1=∠2,
∴∠1=66°.
【点睛】本题考查了三角形内角和定理,平行线的判定和性质等知识点,能熟记平行线的性质和判定定理是解此题的关键.
25.(1)见解析
(2)①见解析;②3.
【分析】(1)将点C向右平移两个单位长度得到点N,则过点M、N的直线即为所求作的直线l;
(2)①根据平移的性质作图即可;
②由题意知,平移过程中点P先向左平移2个单位,再向上平移1个单位,即可得P点经过的路径长.
【详解】(1)解:如图,直线l即为所求.
(2)①如图,即为所求.
②∵点P是△ABC内任意一点,
∴平移过程中,点P先向左平移2个单位,再向上平移1个单位,
∴P点经过的路径长为2+1=3.
故答案为:3.
【点睛】本题考查作图—平移变换,平移的性质,正确找出对应点的位置是解答本题的关键.
26.(1)见解析
(2)见解析
【分析】(1)根据格点的特点,点B向右平移3格,向上平移4格到达点A,因此将点D向右平移3格,向上平移4格到达格点即为点E,连接DE即可;
(2)将点D向左平移1格,向上平移2格到达格点F,连接DF,作出AC的平行线即可.
【详解】(1)解:线段DF即为所求作的线段,如图所示:
(2)解:作线段,
∴,
∵,
∴,
∴,
∴线段DF为所求作的线段,如图所示:
或
【点睛】本题主要考查了平移作图,平行线的性质,根据网格的特点作出与已知线段平行的线段,是解题的关键.
一、单选题
1.(2022春·浙江绍兴·七年级统考期末)据说中国最早的风筝是由古代哲学家墨翟制作的.如图风筝的骨架构成了多种位置关系的角.下列角中与∠1构成同位角的是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.(2022春·浙江湖州·七年级统考期末)如图,∠1和∠2是内错角的是( )
A. B.C. D.
3.(2022春·浙江杭州·七年级统考期末)如图,说法正确的是( )
A.和是内错角 B.和是内错角
C.和是同位角 D.和是同旁内角
4.(2022春·浙江台州·七年级统考期末)在铺设铁轨时,两条直轨必须是互相平行的,如图,已经知道是直角,那么再度量图中已标出的哪个角,不能判断两条直轨是否平行( )
A. B. C. D.
5.(2022春·浙江绍兴·七年级统考期末)在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线,,贝贝、晶晶、欢欢三位同学的做法如图所示:
上述三位同学的做法中,依据“内错角相等,两直线平行”的是( )
A.仅贝贝同学 B.贝贝和晶晶 C.晶晶和欢欢 D.贝贝和欢欢
6.(2022春·浙江嘉兴·七年级统考期末)我们学过用三角尺和直尺画平行线的方法,按如图方式画出的两条直线一定平行,其判定依据是( )
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.两直线平行,同位角相等 D.两直线平行,内错角相等
7.(2022春·浙江台州·七年级统考期末)如图,直线a,b被直线c所截,下列条件中,不能得到的是( )
A.∠1=∠3 B.∠2=∠4
C.∠3+∠4=180° D.∠1+∠4=180°
8.(2022春·浙江温州·七年级统考期末)如图,在科学《光的反射》活动课中,小麦同学将支架平面镜放置在水平桌面MN上,镜面AB的调节角的调节范围为12°~69°,激光笔发出的光束DG射到平面镜上,若激光笔与水平天花板(直线EF)的夹角,则反射光束GH与天花板所形成的角不可能取到的度数为( )
A.129° B.72° C.51° D.18°
9.(2022春·浙江杭州·七年级统考期末)如图,已知∥,,分别平分和,且交于点,则( )
A. B.
C. D.
10.(2022春·浙江湖州·七年级统考期末)如图1,当光线从空气斜入射到某种透明的液体时发生了折射,满足入射角与折射角的度数比为.如图2,在同一平面上,两条光线同时从空气斜射入这种液体中,两条入射光线与水平液面夹角分别为,,在液体中两条折射光线的夹角为,则,,三者之间的数量关系为( )
A. B.
C. D.
11.(2022春·浙江湖州·七年级统考期末)下列现象中属于平移的是( )
①方向盘的转动;②打气筒打气时,活塞的运动;③钟摆的摆动;④汽车雨刷的运动
A.①② B.②③ C.①②④ D.②
12.(2022春·浙江台州·七年级统考期末)下列图案中,由如图所示的图案通过平移后得到的是( )
A.B. C. D.
13.(2022春·浙江绍兴·七年级统考期末)如图,将△ABC沿BC方向平移1cm得到对应的△A′B′C′.若B′C=2cm,则BC′的长是( )
A.2cm B.3cm C.4cm D.5cm
14.(2022春·浙江宁波·七年级统考期末)如图所示,三张正方形纸片①,②,③分别放置于长,宽的长方形中,正方形①,②,③的边长分别为a,b,c,且,则阴影部分周长为( )
A. B. C. D.
二、填空题
15.(2022春·浙江嘉兴·七年级统考期末)如图,直线a,b被直线c所截,的同旁内角是__________.
16.(2022春·浙江台州·七年级统考期末)如图,把一张长方形纸条沿折叠,若,则______°.
17.(2022春·浙江绍兴·七年级校联考期末)如图,已知直线,点,分别在直线,上,点为,之间一点,且点在的右侧,.若与的平分线相交于点,与的平分线相交于点,与的平分线相交于点……以此类推,若,则的值是______.
18.(2022春·浙江金华·七年级统考期末)如图,直线l1∥l2,AB⊥CD,∠1=34°,则∠2=________.
19.(2022春·浙江绍兴·七年级统考期末)生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD=___°.
20.(2022春·浙江绍兴·七年级统考期末)如图,已知ABCD,FE⊥AB于点E,点G在直线CD上,且位于直线EF的右侧.
(1)若∠EFG=120°,则∠FGC的度数是 _____;
(2)若∠AEH=∠FGH=20°,∠H=50°,则∠EFG的度数是 _____.
三、解答题
21.(2022春·浙江湖州·七年级统考期末)长江汛期即将来临,为了便于夜间查看江水及两岸河堤的情况,防汛指挥部在一危险地带两岸各安置了一探照灯(如图1),假定这一带长江两岸河堤是平行的,即,连结,且.灯射线自顺时针旋转至便立即回转,灯射线自顺时针旋转至便立即回转,两灯不停交叉照射巡视.若灯转动的速度是1度/秒,灯转动的速度是3度/秒.
(1)若两灯同时转动,在灯射线第一次转到之前,两灯射出的光线交于点.
①如图1,当两灯光线同时转动50秒时,求的度数.
②如图2,过作交于点,则在转动过程中,求与的比值,并说明理由.
(2)若灯射线先转动30秒,灯射线才开始转动,在灯射线第一次转到之前,灯转动几秒,两灯的光线互相平行?
22.(2022春·浙江衢州·七年级统考期末)已知△ABC与△ADE共顶点A,,顶点B和C在直线上(点B在点C的左侧),顶点D和E在直线上(点D在点E的左侧),且直线.
(1)如图1,顶点A在与之间,判断∠BAD与是否相等,并说明理由.
(2)如图2,顶点A在与之间,∠ABC的外角平分线与∠AED的角平分线交于点F,若,求∠BFE的度数.
(3)若顶点A在直线的下方,且顶点B、A、D不在一条直线上,∠ABC的外角平分线与∠AED的角平分线交于点F,记,,请探究与的数量关系,并直接写出结论.
23.(2022春·浙江台州·七年级统考期末)如图,已知:,.求证:.
证明:∵(已知),
∴____________(________________________).
∴(_____________________________).
∵(已知),
∴(等量代换).
∴____________(__________________________).
∴(______________________________).
24.(2022春·浙江宁波·七年级统考期末)如图,在中,点分别在上,且, .
(1)求证: ;
(2)若平分,,求的度数.
25.(2022春·浙江金华·七年级统考期末)如图是单位长度为1的网格,△ABC的三个顶点都在格点上,点M也在格点上.只用无刻度直尺在网格内按要求完成作图并回答问题:
(1)过点M作平行于BC的直线l.
(2)将图中△ABC先向左平移2个单位,再向上平移1个单位得到.
①作出平移后的;
②点P是三角形ABC内任意一点,则平移过程中P点经过的路径长为 .
26.(2022春·浙江台州·七年级统考期末)如图,在7×5的方格中,三角形ABC的顶点均在格点上,点D为格点.
(1)在图中作出线段DE(E点在格上),使;
(2)在图中作出线段DF(F点在格上),使.
参考答案:
1.A
【分析】根据同位角的定义解答.两条直线被第三条直线所截形成的角中,若两个角都在两直线的同侧,并且在第三条直线(截线)的同旁,则这样一对角叫做同位角.
【详解】解:由图可得,与构成同位角的是.
故选:A.
【点睛】本题主要考查了同位角的定义,解题的关键是明确同位角的边构成“”形,内错角的边构成“”形,同旁内角的边构成“”形.
2.A
【分析】根据内错角的定义:两个角位于截线两侧,且在两条被截线之间的一对角,逐一判断即可.
【详解】解:A图中,∠1与∠2是内错角,符合题意;
B图中,∠1与∠2不在两条被截线之间,不是内错角,不符合题意;
C图中,∠1与∠2是同旁内角,不符合题意;
D图中,∠1与∠2是同位角,不符合题意;
故选:A.
【点睛】本题考查了同位角、内错角、同旁内角的定义,掌握各自的位置关系是解题关键.
3.B
【分析】根据同位角,内错角,同旁内角的定义,逐项判断即可求解.
【详解】解:A、和是同位角,故本选项错误,不符合题意;
B、和是内错角,故本选项正确,符合题意;
C、和是内错角,故本选项错误,不符合题意;
D、和不是同旁内角,故本选项错误,不符合题意;
故选:B
【点睛】本题主要考查了同位角,内错角,同旁内角的定义,熟练掌握两条直线被第三条直线所截,在截线的同旁、被截两直线的同一方,我们把这种位置关系的角称为同位角;两条直线被第三条直线所截,两个角分别在截线的两侧,且夹在两条被截直线之间,具有这样位置关系的一对角叫做内错角;两条直线被第三条直线所截,在两条被截线之间,并在截线同旁的两个角称为同旁内角是解题的关键.
4.A
【分析】因为∠2是直角,只要找出与∠2互为同位角、内错角、同旁内角的其他角,根据平行线的判定定理判定即可得到正确答案.
【详解】因为∠2是直角,∠4和∠2是同位角,如果度量出,
根据“同位角相等,两直线平行”,就可以判断两条直轨平行,
∠5和∠2是内错角,如果度量出,
根据“内错角相等,两直线平行”,就可以判断两条直轨平行,
∠3和∠2是同旁内角,如果度量出,
根据“同旁内角互补,两直线平行”,就可以判断两条直轨平行,
所以答案为:A.
【点睛】本题考查两直线平行的判定定理,解决本题的关键是熟练的掌握平行线的判定定理.
5.D
【分析】根据平行线的判定定理进行判断,即可得到答案.
【详解】解:根据题意,
贝贝:利用内错角相等,两直线平行;
晶晶:利用同位角相等,两直线平行;
欢欢:利用内错角相等,两直线平行;
故选:D.
【点睛】本题考查了平行线的判定与性质.属于基础题,熟记平行线的判定定理即可填空.
6.A
【分析】根据同位角相等,两直线平行,即可求解.
【详解】解:根据题意得:两条直线一定平行,其判定依据是同位角相等,两直线平行.
故选:A
【点睛】本题主要考查了平行线的判定,熟练掌握同位角相等,两直线平行是解题的关键.
7.A
【分析】根据平行线的判定定理判断求解即可.
【详解】解:A.由∠1=∠3,不能判定a∥b,故选项符合题意;
B.∵∠2=∠4,
∴a∥b,
故选项不符合题意;
C.∵∠3+∠4=180°,
∴a∥b,
故选项不符合题意;
D.∵∠1+∠4=180°,∠1=∠3,
∴∠3+∠4=180°,
∴a∥b,
故选项不符合题意;
故选:A.
【点睛】此题考查了平行线的判定,熟记平行线的判定定理是解题的关键.
8.C
【分析】分当时,如图1所示,当时,如图2所示,两种情况,利用平行线的性质求解即可.
【详解】解:当时,如图1所示,过点G作,
∵,
∴,
∴∠PGQ =∠EPG=30°,∠BGQ=∠ABM,
∴∠PGB=∠PGQ+∠BGQ=30°+∠ABM,
由反射定理可知,∠AGH=∠PGB=30°+∠ABM,
∴∠PGH=180°-∠AGH-∠PGB=120°-2∠ABM,
∴∠HGQ=∠PGH+∠PGQ=150°-2∠ABM,
∴∠PHG=180°-∠HGQ=30°+2∠ABM,
∴
当时,如图2所示,过点G作,
同理可得∠PGQ=∠EPG=30°,∠BGQ=∠ABM,∠PHG=∠HGQ,
∴∠AGP=∠HGB=∠HGQ+∠QGB=∠PHG+∠ABM,
∴∠PGH=180°-∠AGP-∠HGB=180°-2∠PHG-2∠ABM,
∴∠HGP=∠PGQ-∠PGH=2∠PHG+2∠ABM-150°,
∴∠PHG=150°-2∠ABM,
∴,
综上所述,或,
故选C.
【点睛】本题主要考查了平行线的性质,正确作出辅助线和利用分类讨论的思想求解是解题的关键.
9.C
【分析】过点作,利用平行线的性质可证得,可以得到与的关系
【详解】解:过点作,如图:
,
∴CD∥EM ,
∴
∵的平分线与的平分线相交于点,
∴,
∴,
∵,
∴
∴
整理得:.
故选:C.
【点睛】本题主要考查了平行线的性质和角平分线,解决问题的关键是作辅助线构造同旁内角以及内错角,依据平行线的性质进行推导计算,解题时注意数形结合思想的运用.
10.B
【分析】过点B、D、F分别作水平线的垂线,则,根据平行线的性质与光的折射原理即可得到答案
【详解】如图:过点B、D、F分别作水平线的垂线,则
由题知
即:
即
故选B
【点睛】本题考查了平行线的性质,光学原理,读懂题并熟练掌握平行线的性质是关键.
11.D
【分析】直接根据平移的定义分别判断.
【详解】解:①方向盘的转动是旋转,故不符合题意;
②打气筒打气时,活塞的运动是平移,故符合题意;
③钟摆的摆动是旋转,故不符合题意;
④汽车雨刷的运动是旋转,故不符合题意;
综上分析可知,属于平移的是②,故D正确.
故选:D.
【点睛】本题考查了生活中的平移现象,熟练掌握平移的定义是解答本题的关键. 平移是指在平面内,将一个图形上的所有点都按照某个方向作相同距离的移动.平移不改变图形的形状和大小,只是改变位置.
12.C
【分析】根据图形平移的性质对各选项进行逐一分析即可.
【详解】解:A.由图中所示的图案通过旋转而成,故A错误,不符合题意;
B.由图中所示的图案与原图案成轴对称,不能通过平移得到,故B错误,不符合题意;
C.由图中所示的图案通过平移而成,故C正确,符合题意;
D.由图中所示的图案通过翻折而成,故D错误,不符合题意.
故选:C.
【点睛】本题主要考查了平移的性质,熟练掌握平移前后图形的形状大小不变,只是改变了位置是解题的关键.
13.C
【分析】据平移的性质可得BB′=CC′=1,列式计算即可得解.
【详解】解:∵△ABC沿BC方向平移1cm得到△A′B′C′,
∴BB′=CC′=1cm,
∵B′C=2cm,
∴BC′= BB′+ B′C+CC′=1+2+1=4(cm).
故选:C.
【点睛】本题考查了平移的性质,熟记性质得到相等的线段是解题的关键.
14.A
【分析】根据平移的性质求出水平边之和及竖直边之和,再列式计算解答.
【详解】解:将阴影部分水平的边通过平移可得水平边之和为:2(a+b),
将阴影部分竖直的边通过平移可得竖直边之和为:2(a+c-b),
∴阴影部分的周长为:2(a+b)+2(a+c b)=2a+2b+2a+2c 2b=4a+2c,
故选:A.
【点睛】此题主要考查了平移的性质,整式的加减,根据平移的性质求出水平边之和及竖直边之和是解题的关键.
15.∠6
【分析】两条直线被第三条直线所截形成的角中,若两个角都在两直线的之间,并且在第三条直线(截线)的同旁,这样的一对角叫做同旁内角.
【详解】解:∵直线a、b被直线c所截,
∴∠3的同旁内角是∠6.
故答案为:∠6.
【点睛】本题主要考查了同旁内角的概念,三线八角中的某两个角是不是同位角、内错角或同旁内角,完全由那两个角在图形中的相对位置决定,同位角的边构成“F”形,内错角的边构成“Z”形,同旁内角的边构成“U”形.
16.65
【分析】先根据已知条件和邻补角的性质得∠DEG=130°,再由折叠的性质得到∠DEF=∠FEG=∠DEG,再根据平行线的性质得到∠DEF=65°即可.
【详解】解:∵∠AEG=50°,
∴∠DEG=180°-50°=130°,
∵把一张长方形纸片ABCD沿EF折叠,
∴∠DEF=∠FEG=∠DEG=65°,
∵四边形ABCD是长方形,
∴ADBC,
∴∠DEF=65°.
故答案为:65.
【点睛】此题考查了折叠的性质以及平行线的性质,解题的关键是熟练掌握折叠与平行线的性质,找到相等的角.
17.4
【分析】作EF//AB则AB//CD//EF,根据平行线的性质得出∠MEN=∠BME+∠DME=128°,同理∠ME1N=(∠BME+∠DME) =64°,∠ME2N=(∠BME1+∠DME1) =32°,可归纳规律∠ME=(∠BME-1+∠DME-1) =,依此建立方程=8°求解即可解答.
【详解】解:如图:作EF//AB
∵AB//CD
∴AB//CD//EF
∴∠FEM=∠BME, ∠FEN=∠DNE,
∴∠MEN=∠BME+∠DME=∠FEM +∠FEN =∠MEN= 128°
同理:ME1N=(∠BME+∠DME) =64°,
∠ME2N=(∠BME1+∠DME1) =32°
…
∠ME=(∠BME-1+∠DME-1) =
由题意得:=8°,解得n=4.
故答案为4.
【点睛】本题考查了平行线的性质、探索图形规律、角平分线的定义等知识点,正确的识别图形、归纳图形规律是解答本题的关键.
18.56°/56度
【分析】由可得,由可得.
【详解】解:,
,
又,
,
,
.
故答案为:.
【点睛】本题考查了平行线的性质、垂直的定义,熟练掌握相关性质定理是解题的关键.
19.270
【分析】过点B作BF∥AE,从而得到CD∥AE∥BF,根据平行线的性质得到∠BCD+∠CBF=180°,∠ABF=90°,即可得到结论.
【详解】如图,过点B作BF∥AE,
∵CD∥AE,
∴CD∥AE∥BF,
∴∠BCD+∠CBF=180°,∠ABF+∠BAE=180°,
∵AB⊥AE,
∴∠BAE=90°,
∴∠ABF=90°,
∴∠ABC+∠BCD=∠ABF+∠CBF+∠BCD= 90°+180°=270°.
故答案为:270.
【点睛】本题主要考查了平行线的判定与性质,正确作出辅助线,熟记平行线的性质是解题的关键.
20. 30°/30度 140°/140度
【分析】(1)过点F作FM∥AB,根据平行线的性质求解即可;
(2)过点F作FM∥AB,过点H作HN∥AB,根据平行线的性质求解即可.
【详解】解:(1)过点F作FM∥AB,
∵FE⊥AB,FM∥AB,
∴FE⊥FM,
∴∠EFM=90°,
∵∠EFG=120°,
∴∠MFG=∠EFG∠EFM=30°,
∵FM∥AB,AB∥CD,
∴FM∥CD,
∴∠FGC=∠MFG=30°,
故答案为:30°;
(2)过点F作FM∥AB,过点H作HN∥AB,
∴∠AEH=∠EHN=20°,
∵∠EHG=50°,
∴∠NHG=∠EHG-∠EHN=30°,
∵HN∥AB,AB∥CD,
∴HN∥CD,
∴∠CGH=∠NHG=30°,
∵∠FGH=20°,
∴∠FGC=∠CGH+∠FGN=50°,
根据(1)知,∠EFM=90°,∠FGC=∠MFG,
∴∠MFG=50°,
∴∠EFG=∠EFM+∠MFG=140°,
故答案为:140°.
【点睛】此题考查了平行线的性质,熟记平行线的性质定理是解题的关键.
21.(1)①;②比值为,详见解析
(2)灯转动15秒或82.5秒时,两灯的光束互相平行
【分析】(1)①当转动50秒时,有,即有,根据,即可得解;②过点作,得到,,即有,,根据,可得,再根据,可得,即问题得解;
(2)设A灯转动秒,两灯的光束互相平行,A灯先转动30秒,则AQ转到AP还需要180-30=150(秒)即,①当B射线第一次垂直MN时,用时90÷3=30(秒),此时A射线共计运动30+30=60秒,即,即在灯射线到达之前,先证明,即有:,即可求解;②在灯射线到达之后,回到前,根据①中,同理有:,即有:,即可求解;③在灯射线回到后,第二次到前,由题意得:,即可求解,即问题得解.
【详解】(1)两灯速度为:灯A转动的速度是1度/秒,灯B转动的速度是3度/秒.
①当转动50秒时,,
∴,
∴,
故答案为:15°;
②比值为:,理由如下,
如图2,过点作,
∵,
∴,
设两灯转动时间为秒,则,,
∴,,
∴,
即,
又∵,
即,
而,
∴
.
∴.
即比值为:;
(2)两灯速度为:灯A转动的速度是1度/秒,灯B转动的速度是3度/秒.
设A灯转动秒,两灯的光束互相平行,
A灯先转动30秒,则AQ转到AP还需要180-30=150(秒)
即,
①当B射线第一次垂直MN时,用时90÷3=30(秒),
此时A射线共计运动30+30=60秒,即,
即在灯射线到达之前,如图3所示,
∵,,
∴,,
∴,
∴,
即有:,
解得:(秒);
②如图4,在灯射线到达之后,回到前,
根据①中,同理有:
∵
即有:,
解得:.
③如图5,在灯射线回到后,第二次到前,
由题意得:
,解得:(舍去).
综上所述,灯转动15秒或82.5秒时,两灯的光束互相平行.
【点睛】本题主要考查了平行线的性质以及角的和差关系,厘清角度之间的关系并注意分类讨论是解答本题的关键.
22.(1),理由见解析
(2)100°
(3)或
【分析】(1)过点A作,根据平行线的性质直接求解即可得到结论;
(2)根据(1)中的方法可知,,根据角平分线的性质及邻补角的定义等量代换即可得到结论;
(3)令,根据角平分线定义得,,过作,过作,得到,从而根据点与的关系分五种情况求解,由角度和差关系得到,或,联立方程组得到或者.
【详解】(1)解:.
过点A作,如图所示:
,
∴,
∴,
,
∴,
∴;
(2)解:如图所示:
由(1)可知,
同(1)理可得,
∵BF平分∠ABH,EF平分∠AED,
∴,
∵,
∴,,
;
(3)解:根据点与的关系分五种情况求解:
1..点在的边左侧,如图所示:
令,则根据角平分线定义得,,
过作,过作,则,
,,
①,
在中,,
,
,
②,
由①得,
由②得,
将①代入②得;
2.点在的边上,如图所示:
令,则根据角平分线定义得,,
过作,过作,则,
,,
①,
在中,,
,
,
②,
由①得,
由②得,
将①代入②得;
3.点在内,如图所示:
令,则根据角平分线定义得,,
过作,过作,则,
,,
①,
在中,,
,
,
②,
由①得,
由②得,
将①代入②得;
4.点在的边上,,如图所示:
令,则根据角平分线定义得,,
过作,过作,则,
,,
①,
在中,,
,
,
②,
由①得,
由②得,
将①代入②得,
,,满足;
5.点在的边右侧,如图所示:
令,则根据角平分线定义得,,
过作,过作,则,
,,
①,
在中,,
,
,
②,
由①得,
由②得,
将①代入②得;
综合上述1、2、3、4、5可得或.
【点睛】本题考查平行线的性质,涉及到角平分线的性质、邻补角定义、直角三角形锐角互余等性质,根据题意作出辅助线,分类讨论并根据图形恰当表示出各角之间的关系是解决问题的关键.
23.DE;AF;同位角相等,两直线平行;两直线平行,同位角相等;AB;CD;内错角相等,两直线平行;两直线平行,内错角相等
【分析】先通过已知条件证明DEAF,再由两直线平行同位角相等和等量代换证出ABCD,再根据两直线平行,内错角相等得出.
【详解】证明:∵(已知),
∴DEAF(同位角相等,两直线平行).
∴(两直线平行,同位角相等).
∵(已知),
∴(等量代换).
∴ABCD(内错角相等,两直线平行).
∴(两直线平行,内错角相等).
故答案为:DE;AF;同位角相等,两直线平行;两直线平行,同位角相等;AB;CD;内错角相等,两直线平行;两直线平行,内错角相等.
【点睛】本题考查平行线的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.
24.(1)见解析
(2)
【分析】(1)根据平行线的性质得出∠1=∠C,求出∠2=∠C,再根据平行线的判定得出即可;
(2)根据平行线的性质得出∠B+∠BAF=180°,求出∠BAF,根据角平分线的定义救出∠2,再求出∠1即可.
【详解】(1)∵DEAC,
∴∠1=∠C,
∵∠1=∠2,
∴∠2=∠C,
∴AFBC;
(2)∵AFBC,
∴∠B+∠BAF=180°,
∵∠B=48°,
∴∠BAF=180°-48°=132°,
∵AC 平分∠BAF,
∴∠2=∠BAF=66°,
∵∠1=∠2,
∴∠1=66°.
【点睛】本题考查了三角形内角和定理,平行线的判定和性质等知识点,能熟记平行线的性质和判定定理是解此题的关键.
25.(1)见解析
(2)①见解析;②3.
【分析】(1)将点C向右平移两个单位长度得到点N,则过点M、N的直线即为所求作的直线l;
(2)①根据平移的性质作图即可;
②由题意知,平移过程中点P先向左平移2个单位,再向上平移1个单位,即可得P点经过的路径长.
【详解】(1)解:如图,直线l即为所求.
(2)①如图,即为所求.
②∵点P是△ABC内任意一点,
∴平移过程中,点P先向左平移2个单位,再向上平移1个单位,
∴P点经过的路径长为2+1=3.
故答案为:3.
【点睛】本题考查作图—平移变换,平移的性质,正确找出对应点的位置是解答本题的关键.
26.(1)见解析
(2)见解析
【分析】(1)根据格点的特点,点B向右平移3格,向上平移4格到达点A,因此将点D向右平移3格,向上平移4格到达格点即为点E,连接DE即可;
(2)将点D向左平移1格,向上平移2格到达格点F,连接DF,作出AC的平行线即可.
【详解】(1)解:线段DF即为所求作的线段,如图所示:
(2)解:作线段,
∴,
∵,
∴,
∴,
∴线段DF为所求作的线段,如图所示:
或
【点睛】本题主要考查了平移作图,平行线的性质,根据网格的特点作出与已知线段平行的线段,是解题的关键.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
