5.5.1 分式方程的解法 课件（27张PPT）

(共27张PPT)
5.5.1 分式方程
——分式方程的解法
教 学 目 标
热 身 训 练，回 顾 基 础
探 究 新 知，共 析 例 题
举 一 反 三，变 式 训 练
链 接 中 考，原 题 呈 现
融 汇 贯 通，知 识 总 结
勇 于 挑 战，拓 展 提 升
目 录
教 学 目 标
1、了解分式方程的概念。
2、会解可化为一元一次方程的分式方程。
3、了解增根的概念，会对分式方程的根进行检验。
热 身 训 练，回 顾 基 础
整式方程:
等号两边都是整式的方程.
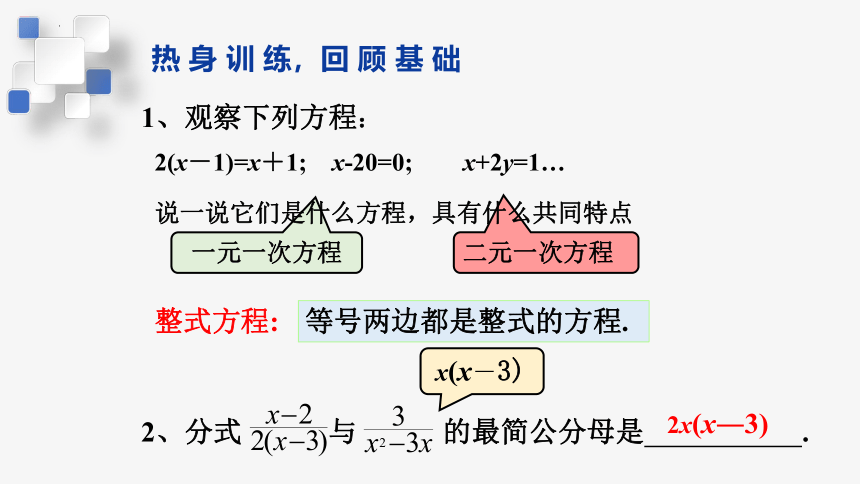
1、观察下列方程：
一元一次方程
二元一次方程
2(x－1)=x＋1; x-20=0; x+2y=1…
说一说它们是什么方程，具有什么共同特点
x(x―3)
2x(x―3)
2、分式 与 的最简公分母是 .
热 身 训 练，回 顾 基 础
解方程：
解一元一次方程的一般步骤：
（1）去分母
（2）去括号
（3）移项
（4）合并同类项
（5）方程两边同除以未知数的系数
某地电话公司调低了长途电话的话费标准，每分费用降低了25％，因此按原收费标准6元话费的通话时间，在新收费标准下可多通话5分时间，问前后两种收费标准每分收费各是多少
主要等量关系是什么
6元话费：
按原收费标准的通话时间＋5＝ 按新收费标准的通话时间
＝
＋5
如果设原来的收费标准是 元／分，可列怎样的方程
合作学习
探 究 新 知，共 析 例 题
探 究 新 知，共 析 例 题
＝
＋5
只含分式，或分式和整式，并且分母中含未知数的方程
叫做分式方程。
分式方程
探 究 新 知，共 析 例 题
（1）是等式；
（2）方程中含有分母；
（3）分母中含有未知数.
分式方程的特征
判断方法：主要是看分母中是否含有未知数
(注意：π不是未知数)．
探 究 新 知，共 析 例 题
下列方程中，哪些是分式方程？哪些不是分式方程？
不是
不是
是
是
是
不是
是
不是
不是
举 一 反 三，变 式 训 练
找一找：
下列方程中属于分式方程的有（ ）;
属于一元分式方程的有（ ）.
① ②
③ ④ x2 +2x-1=0
① ③
①
探 究 新 知，共 析 例 题
解分式方程：
方程两边同乘以4（2x-5),
得4 x+3
( )
= 3 2x-5 .
( )
去括号，得4x+12
= 6x-15.
移项，合并同类项，得2x = 27
x =13.5
把x=13.5代入原方程检验：
左边=
=
=
=右边，
∴x =13.5是原方程的根。
分式方程
整式方程
解整式方程
检 验
转化
最简公分母
结 论
探 究 新 知，共 析 例 题
解方程
方程两边同乘以最简公分母(x-3),
解整式方程,得 x = 3
检验:把x = 3 代入原方程
结果使原方程的最简公分母x-3=0 ,分式无意义，
因此x = 3不是原方程的根.
∴ 原方程无解 .
① ② ③
得 2-x=-1-2(x-3).
增根
使分母为零的根
探 究 新 知，共 析 例 题
验根的方法：将方程的解代入最简公分母，
使分母为零的根叫增根。
增根的定义
增根:在去分母,将分式方程转化为整式方程的过程中出现的不适合于原方程的根.
产生的原因:分式方程两边同乘以一个零因式后,所得的根是整式方程的根,而不是分式方程的根.
····
····
使分母为零的根
······
···
必须检验
举 一 反 三，变 式 训 练
1、分式方程 的最简公分母是 .
2、如果 有增根,那么增根为 .
x=2
x-1
3、关于x的方程 =4 的解是x = ,则a= .
2
举 一 反 三，变 式 训 练
4、解方程:
解:方程两边同乘以最简公分母 ,
化简,得 .
解得 x1= , x2= .
检验:把 x1= ,代入最简公分母,
x(x-2)= = ≠0;
把 x2= ,代入最简公分母,
x(x-2)= =0
x(x-2)
x 2+ x -6=0 或x(x+1)-6=0
-3 2
-3
-3(-3-2) 15
2
2(2-2)
2
-3
① ② ③
∴x = 是增根,舍去.
∴原方程的根是x = .
探 究 新 知，共 析 例 题
解下列方程：
① ； ② ；
③ .
① x = ② x =-3
③ x =-2 (x =1是增根,已舍去)
探 究 新 知，共 析 例 题
解分式方程的一般步骤：
1．在方程的两边都乘以最简公分母，约去分母
化成整式方程．
2．解整式方程．
3．验根．
(1)把未知数的值代入原方程(一般方法)
(2)把未知数的值代入最简公分母(简便方法).
一化二解三检验
探 究 新 知，共 析 例 题
解分式方程容易犯的错误主要有：
(1)去分母时，原方程的整式部分漏乘．
(2)约去分母后，分子是多项式时， 要注意添括号
(3)增根不舍掉.
(4)……
探 究 新 知，共 析 例 题
解：方程两边同乘以（x-2）,
得1-x=-k-2 x-2
( )
去括号，得1-x=-k-2x+4
移项，合并同类项，得x=3-k
3-k=2
k=1
要使方程有增根(无解），必须使分母x-2=0,即x=2.
拓展：若关于x的方程 有增根，则增根可能是什么？此时k的取值是多少？
反思：
分式方程产生增根，即代入分母等于0
将原分式方程去分母后，代入增根.
举 一 反 三，变 式 训 练
解：∵原分式方程有增根，∴x(x－1)＝0.
解得x＝0或x＝1.
∵x＝0不可能是整式方程(a＋2)x＝3的根，
∴原分式方程的增根为x＝1.∴(a＋2)×1＝3.解得a＝1.
解：去分母并整理，得(a＋2)x＝3.
因为x＝1是原方程的增根，所以(a＋2)×1＝3.解得a＝1.
(1)若方程的增根为x＝1，求a的值；
(2)若方程有增根，求a的值；
举 一 反 三，变 式 训 练
①当a＋2＝0时，整式方程(a＋2)x＝3无解．
a＝－2.
②当a＋2≠0时，要使原方程无解，
则x(x－1)＝0.
解得x＝0或x＝1.
把x＝0代入整式方程，a的值不存在；
把x＝1代入整式方程，得a＝1.
综合①②得a的值为－2或1.
(3)若方程无解，求a的值．
链 接 中 考，原 题 呈 现
链 接 中 考，原 题 呈 现
[2022·嘉兴中考] 解方程： .
解：两边同乘 ，得 ，
解得 .
经检验，当 时， ，
所以 是原分式方程的根.
融 汇 贯 通，知 识 总 结
解分式方程的一般步骤.
增根与验根.
增根及增根产生的原因.
解分式方程容易发生的错误.
在解分式方程中你有何收获与体会.
要注意灵活运用解分式方程的步骤.
同时要有简算意识,提高运算的速度和准确性.
体会数学转化的思想方法.
勇 于 挑 战，拓 展 提 升
C
C
勇 于 挑 战，拓 展 提 升
PPT模板下载：www./moban/ 行业PPT模板：www./hangye/
节日PPT模板：www./jieri/ PPT素材下载：www./sucai/
PPT背景图片：www./beijing/ PPT图表下载：www./tubiao/
优秀PPT下载：www./xiazai/ PPT教程： www./powerpoint/
Word教程： www./word/ Excel教程：www./excel/
资料下载：www./ziliao/ PPT课件下载：www./kejian/
范文下载：www./fanwen/ 试卷下载：www./shiti/
教案下载：www./jiaoan/ PPT论坛：www.
感 谢 观 看！