5.5.2 分式方程的应用 课件(28张PPT)
文档属性
| 名称 | 5.5.2 分式方程的应用 课件(28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 468.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-10 16:12:53 | ||
图片预览







文档简介
(共28张PPT)
5.5.2 分式方程
——分式方程的应用
教 学 目 标
热 身 训 练,回 顾 基 础
探 究 新 知,共 析 例 题
举 一 反 三,变 式 训 练
链 接 中 考,原 题 呈 现
融 汇 贯 通,知 识 总 结
勇 于 挑 战,拓 展 提 升
目 录
教 学 目 标
1、经历将实际问题中的等量关系用分式方程表示
的过程。
2、掌握列分式方程解应用题的一般步骤。
3、会列出分式方程解决简单的应用题,提高学生
分析问题、解决问题的能力,培养学生的应用
意识。
热 身 训 练,回 顾 基 础
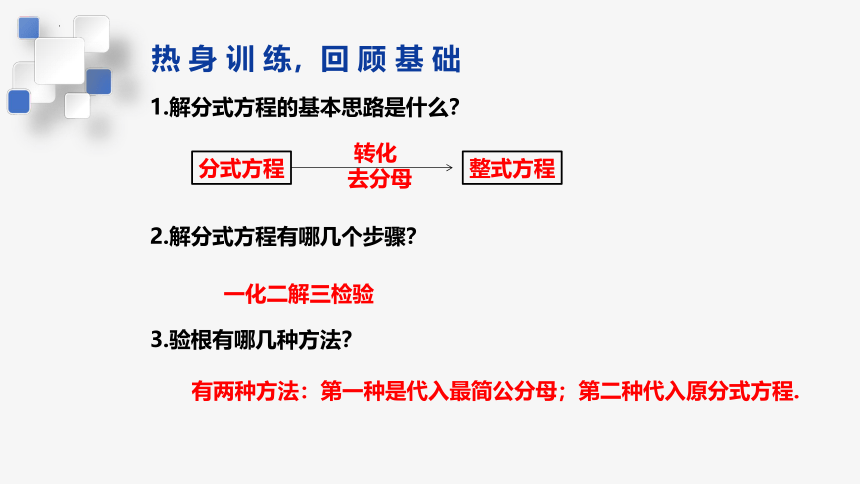
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
3.验根有哪几种方法?
分式方程
整式方程
转化
去分母
一化二解三检验
有两种方法:第一种是代入最简公分母;第二种代入原分式方程.
热 身 训 练,回 顾 基 础
确定最简公分母,去分母,化为一元一次整式
两边同乘以 得:
把x=-3代入最简公分母检验:
(1-x)(1+x)
(1-x)(1+x)
解:
所以 x=-3
所以X=-3是原方程的根。
热 身 训 练,回 顾 基 础
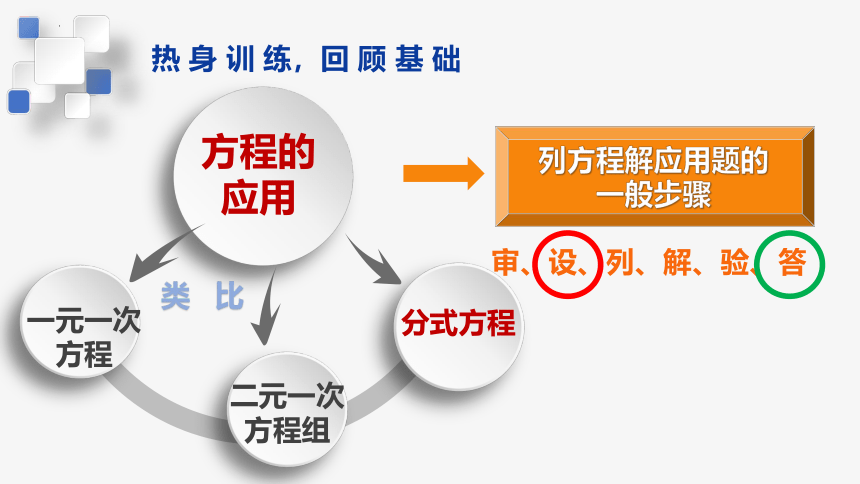
二元一次方程组
分式方程
方程的应用
类 比
一元一次方程
列方程解应用题的
一般步骤
审、设、列、解、验、答
热 身 训 练,回 顾 基 础
某人上山和下山的路程都是s千米,上山的速度为a千米/小时,下山的速度为b千米/小时,则此人上山和下山的平均速度为( )
C
探 究 新 知,共 析 例 题
A、B两地相距40千米,甲从A地到B地,若每小时走x千米,那么需走 小时;如果每小时多走2千米,那么,需走 小时,这样可比原先早 小时到达B地。
探 究 新 知,共 析 例 题
如果分数 的分子分母同时加上同一个数后,
分数的值变为它的倒数,那么加上的这个数是
多少
解 :设这个数为x,则可列方程 。
探 究 新 知,共 析 例 题
某地水稻种植基地在A、B两个面积相同的试验田里种植不同品种的水稻,分别收获16.8吨和13.2吨。已知A试验田的水稻比B试验田的水稻每公顷多收获3吨,分别求
A、B两个试验田每公顷的水稻产量。
(2)本题等量关系是什么?
怎么设元?
根据等量关系你能列出方程吗?
(1)基本数量关系:
A、B两块试验田的面积相等
探 究 新 知,共 析 例 题
解: 设A试验田产量为每公顷x吨,
则B试验田产量为每公顷(x-3)吨.
由题意,得
解这个方程,得x=14
经检验,x=14是所列方程的根,且符合题意。
14-3=11(吨).
答:A试验田的产量是每公顷14吨,
B试验田的产量是每公顷11吨。
探 究 新 知,共 析 例 题
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:求出所列方程的解.
5.验:有二次检验.
(1)是不是所列方程的解;
(2)是否满足实际意义.
6.答:注意单位和语言完整.且答案要生活化.
举 一 反 三,变 式 训 练
甲、乙两人每小时共能做35个零件。甲、乙两人同时开始工作,当甲做了90个零件时,乙做了120个。问甲、乙每小时各做多少个零件?
课内练习
1
解:设甲每时能做x个电器零件,则乙每时能做 个零件。
(35-x)
90
x
120
35-x
=
解得 x=15
经检验,x=15是所列方程的根,且符合题意
35-x=35-15=20
答:甲每时能做15个,
乙每时能做20个.
举 一 反 三,变 式 训 练
此题的等量关系有哪些?
今年的用水单价=去年用水单价×(1+1/3).
每个月的用水量×水的单价=每个月的用水费.
今年2月份的用水量—去年12月份的用水量=5m3.
某市从今年1月1日起调整居民用水价格,每m 水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5m,求我市今年居民用水的价格
举 一 反 三,变 式 训 练
解:设该市去年用水的价格为x元/m3,则今年的水价为(1+1/3)x元/m3,根据题意得
解得 x=1.5.
经检验,x=1.5是原方程的根.
1.5×4/3=2(元)
答:该市今年居民用水的价格为2元/m3.
探 究 新 知,共 析 例 题
照相机成像应用了一个重要原理,即 (V≠f),
其中f表示照相机镜头的焦距,u表示物体到镜头的距离,v表示明胶片(像)到镜头的距离,如果一架照相机f已固定,那么就要依靠调整u、v来使成像清晰。
如果用焦距f=35mm的相机拍摄离镜头的跳高u=2m的花卉,成像清晰,那么拍摄时胶片到镜头的距离v大约是多少?(精确到0.1mm)
探 究 新 知,共 析 例 题
如果用焦距f=35mm的相机拍摄离镜头的跳高u=2m的花卉,成像清晰,那么拍摄时胶片到镜头的距离v大约是多少?(精确到0.1mm)
(V≠f)
解 : 由 ,得
∴
答:此时胶片到镜头的距离约为35.6mm.
举 一 反 三,变 式 训 练
变式:照相机成像应用了一个重要原理,即 (v≠f),问在f、v已知的情况下,怎样确定物体到镜头的距离u?
分析:本题就是利用解分式方程把已知公式变形。
把f、v看成已知数,u看成未知数,解关于u的分式方程。
举 一 反 三,变 式 训 练
移项,得
∴当f≠v时,
检验:因为v,f不为零,f≠v,所以 是分式方程 的根.
答:在已知f,v的情况下,物体到镜头的距离u可以由公式 来确定.
探 究 新 知,共 析 例 题
公式变形:
把要求表示的字母看成未知数,其它字母看成已知数,按解方程的思想来进行解答。
举 一 反 三,变 式 训 练
×
(1+ax≠0)
x
1
a
1
b
=
+
∴
∴
x
1
a
1
b
=
+
a
∴
a
b
=
x
1
+
a
将公式x= (1+ax≠0)变形成已知x,a,求b.
a-b
ab
解: 由x=
a-b
ab
∴ x+ =
1
a
1
b
下面的公式变形对吗?如果不对,应怎样改正?
去年新生婴儿数减去年死亡人数的差与年平均人口数的比叫做年人口的自然增长率,如果用p表示年新生婴儿数,q表示死亡人数,s表示年平均人口数,k表示年人口自然增长率,则年人口自然增长率k=
(1)把公式变形成已知k,p,q,求s的公式。
(2)把公式变形成已知k,s,p,求q的公式
举 一 反 三,变 式 训 练
链 接 中 考,原 题 呈 现
链 接 中 考,原 题 呈 现
融 汇 贯 通,知 识 总 结
分式方程的应用:
列分式方程解应用题.
利用解分式方程把已知公式变形.
勇 于 挑 战,拓 展 提 升
某商店销售一批服装,每件售价150元,可获利25%,求这种服装的成本价.设这种服装的成本价为x元,则得到方程( )
A.x=150×25% B.25%×x=150
C. D.150﹣x=25%
C
利润问题:利润=售价-进价,利润率= ×100%
利润=150-x
分式方程
整式方程
勇 于 挑 战,拓 展 提 升
现有甲,乙,丙三种糖果混合而成的什锦糖果50千克,其中各种糖果的千克数和单价如下表:
甲种糖果 乙种糖果 丙种糖果
千克数 10 20 20
单价(元/千克) 25 20 15
商店以糖果的平均价作为什锦糖的单价,若要使什锦糖的单价提高1元/千克,问需加入甲种糖多少千克?(列方程)
设需加入甲种糖果x千克,可得方程:
PPT模板下载:/moban/ 行业PPT模板:/hangye/
节日PPT模板:/jieri/ PPT素材下载:/sucai/
PPT背景图片:/beijing/ PPT图表下载:/tubiao/
优秀PPT下载:/xiazai/ PPT教程: /powerpoint/
Word教程: /word/ Excel教程:/excel/
资料下载:/ziliao/ PPT课件下载:/kejian/
范文下载:/fanwen/ 试卷下载:/shiti/
教案下载:/jiaoan/ PPT论坛:www.
感 谢 观 看!
5.5.2 分式方程
——分式方程的应用
教 学 目 标
热 身 训 练,回 顾 基 础
探 究 新 知,共 析 例 题
举 一 反 三,变 式 训 练
链 接 中 考,原 题 呈 现
融 汇 贯 通,知 识 总 结
勇 于 挑 战,拓 展 提 升
目 录
教 学 目 标
1、经历将实际问题中的等量关系用分式方程表示
的过程。
2、掌握列分式方程解应用题的一般步骤。
3、会列出分式方程解决简单的应用题,提高学生
分析问题、解决问题的能力,培养学生的应用
意识。
热 身 训 练,回 顾 基 础
1.解分式方程的基本思路是什么?
2.解分式方程有哪几个步骤?
3.验根有哪几种方法?
分式方程
整式方程
转化
去分母
一化二解三检验
有两种方法:第一种是代入最简公分母;第二种代入原分式方程.
热 身 训 练,回 顾 基 础
确定最简公分母,去分母,化为一元一次整式
两边同乘以 得:
把x=-3代入最简公分母检验:
(1-x)(1+x)
(1-x)(1+x)
解:
所以 x=-3
所以X=-3是原方程的根。
热 身 训 练,回 顾 基 础
二元一次方程组
分式方程
方程的应用
类 比
一元一次方程
列方程解应用题的
一般步骤
审、设、列、解、验、答
热 身 训 练,回 顾 基 础
某人上山和下山的路程都是s千米,上山的速度为a千米/小时,下山的速度为b千米/小时,则此人上山和下山的平均速度为( )
C
探 究 新 知,共 析 例 题
A、B两地相距40千米,甲从A地到B地,若每小时走x千米,那么需走 小时;如果每小时多走2千米,那么,需走 小时,这样可比原先早 小时到达B地。
探 究 新 知,共 析 例 题
如果分数 的分子分母同时加上同一个数后,
分数的值变为它的倒数,那么加上的这个数是
多少
解 :设这个数为x,则可列方程 。
探 究 新 知,共 析 例 题
某地水稻种植基地在A、B两个面积相同的试验田里种植不同品种的水稻,分别收获16.8吨和13.2吨。已知A试验田的水稻比B试验田的水稻每公顷多收获3吨,分别求
A、B两个试验田每公顷的水稻产量。
(2)本题等量关系是什么?
怎么设元?
根据等量关系你能列出方程吗?
(1)基本数量关系:
A、B两块试验田的面积相等
探 究 新 知,共 析 例 题
解: 设A试验田产量为每公顷x吨,
则B试验田产量为每公顷(x-3)吨.
由题意,得
解这个方程,得x=14
经检验,x=14是所列方程的根,且符合题意。
14-3=11(吨).
答:A试验田的产量是每公顷14吨,
B试验田的产量是每公顷11吨。
探 究 新 知,共 析 例 题
列分式方程解应用题的一般步骤
1.审:分析题意,找出数量关系和相等关系.
2.设:选择恰当的未知数,注意单位和语言完整.
3.列:根据数量和相等关系,正确列出代数式和方程.
4.解:求出所列方程的解.
5.验:有二次检验.
(1)是不是所列方程的解;
(2)是否满足实际意义.
6.答:注意单位和语言完整.且答案要生活化.
举 一 反 三,变 式 训 练
甲、乙两人每小时共能做35个零件。甲、乙两人同时开始工作,当甲做了90个零件时,乙做了120个。问甲、乙每小时各做多少个零件?
课内练习
1
解:设甲每时能做x个电器零件,则乙每时能做 个零件。
(35-x)
90
x
120
35-x
=
解得 x=15
经检验,x=15是所列方程的根,且符合题意
35-x=35-15=20
答:甲每时能做15个,
乙每时能做20个.
举 一 反 三,变 式 训 练
此题的等量关系有哪些?
今年的用水单价=去年用水单价×(1+1/3).
每个月的用水量×水的单价=每个月的用水费.
今年2月份的用水量—去年12月份的用水量=5m3.
某市从今年1月1日起调整居民用水价格,每m 水费上涨三分之一,小丽家去年12月的水费是15元,今年2月的水费是30元.已知今年2月的用水量比去年12月的用水量多5m,求我市今年居民用水的价格
举 一 反 三,变 式 训 练
解:设该市去年用水的价格为x元/m3,则今年的水价为(1+1/3)x元/m3,根据题意得
解得 x=1.5.
经检验,x=1.5是原方程的根.
1.5×4/3=2(元)
答:该市今年居民用水的价格为2元/m3.
探 究 新 知,共 析 例 题
照相机成像应用了一个重要原理,即 (V≠f),
其中f表示照相机镜头的焦距,u表示物体到镜头的距离,v表示明胶片(像)到镜头的距离,如果一架照相机f已固定,那么就要依靠调整u、v来使成像清晰。
如果用焦距f=35mm的相机拍摄离镜头的跳高u=2m的花卉,成像清晰,那么拍摄时胶片到镜头的距离v大约是多少?(精确到0.1mm)
探 究 新 知,共 析 例 题
如果用焦距f=35mm的相机拍摄离镜头的跳高u=2m的花卉,成像清晰,那么拍摄时胶片到镜头的距离v大约是多少?(精确到0.1mm)
(V≠f)
解 : 由 ,得
∴
答:此时胶片到镜头的距离约为35.6mm.
举 一 反 三,变 式 训 练
变式:照相机成像应用了一个重要原理,即 (v≠f),问在f、v已知的情况下,怎样确定物体到镜头的距离u?
分析:本题就是利用解分式方程把已知公式变形。
把f、v看成已知数,u看成未知数,解关于u的分式方程。
举 一 反 三,变 式 训 练
移项,得
∴当f≠v时,
检验:因为v,f不为零,f≠v,所以 是分式方程 的根.
答:在已知f,v的情况下,物体到镜头的距离u可以由公式 来确定.
探 究 新 知,共 析 例 题
公式变形:
把要求表示的字母看成未知数,其它字母看成已知数,按解方程的思想来进行解答。
举 一 反 三,变 式 训 练
×
(1+ax≠0)
x
1
a
1
b
=
+
∴
∴
x
1
a
1
b
=
+
a
∴
a
b
=
x
1
+
a
将公式x= (1+ax≠0)变形成已知x,a,求b.
a-b
ab
解: 由x=
a-b
ab
∴ x+ =
1
a
1
b
下面的公式变形对吗?如果不对,应怎样改正?
去年新生婴儿数减去年死亡人数的差与年平均人口数的比叫做年人口的自然增长率,如果用p表示年新生婴儿数,q表示死亡人数,s表示年平均人口数,k表示年人口自然增长率,则年人口自然增长率k=
(1)把公式变形成已知k,p,q,求s的公式。
(2)把公式变形成已知k,s,p,求q的公式
举 一 反 三,变 式 训 练
链 接 中 考,原 题 呈 现
链 接 中 考,原 题 呈 现
融 汇 贯 通,知 识 总 结
分式方程的应用:
列分式方程解应用题.
利用解分式方程把已知公式变形.
勇 于 挑 战,拓 展 提 升
某商店销售一批服装,每件售价150元,可获利25%,求这种服装的成本价.设这种服装的成本价为x元,则得到方程( )
A.x=150×25% B.25%×x=150
C. D.150﹣x=25%
C
利润问题:利润=售价-进价,利润率= ×100%
利润=150-x
分式方程
整式方程
勇 于 挑 战,拓 展 提 升
现有甲,乙,丙三种糖果混合而成的什锦糖果50千克,其中各种糖果的千克数和单价如下表:
甲种糖果 乙种糖果 丙种糖果
千克数 10 20 20
单价(元/千克) 25 20 15
商店以糖果的平均价作为什锦糖的单价,若要使什锦糖的单价提高1元/千克,问需加入甲种糖多少千克?(列方程)
设需加入甲种糖果x千克,可得方程:
PPT模板下载:/moban/ 行业PPT模板:/hangye/
节日PPT模板:/jieri/ PPT素材下载:/sucai/
PPT背景图片:/beijing/ PPT图表下载:/tubiao/
优秀PPT下载:/xiazai/ PPT教程: /powerpoint/
Word教程: /word/ Excel教程:/excel/
资料下载:/ziliao/ PPT课件下载:/kejian/
范文下载:/fanwen/ 试卷下载:/shiti/
教案下载:/jiaoan/ PPT论坛:www.
感 谢 观 看!
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
