浙教版七年级下册 2.1 二元一次方程 课件(共13张PPT)
文档属性
| 名称 | 浙教版七年级下册 2.1 二元一次方程 课件(共13张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 19:49:23 | ||
图片预览





文档简介
(共13张PPT)
1.请同学们回顾一下,我们已经学习了哪类方程?请举一个例子.
2.在学习这类方程时,我们学习了它的哪些相关知识?
3.请给你举的例子,加上情境,编成一道应用题.
课前作业,回顾旧知
概念
解法
应用
2.1 二元一次方程
根据题意列出方程:
(2)七年级二班男生人数的两倍比女生人数的三倍多七人,求男生、女生的人数.设男生人数为a,女生人数为b,则列出方程 .
问题引入,章节起始
(1)篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分,如果甲队在这次比赛中一共得了16分,求甲队在这次比赛中胜负各几场?设甲队胜x场,负y场,则列出方程 .
请你根据一元一次方程的特征,类比得出二元一次方程的概念.
一元一次方程
二元一次方程
1.含有一个未知数;
2.未知数的指数是一次;
3.等式两边都是整式.
2.含有未知数的项的次数都是一次;
二元一次方程的概念:
含有两个未知数,且含有未知数的项的次数都是一次的方程叫做二元一次方程.
类比思想
3.等式两边都是整式.
1.含有两个未知数;
深入探究,形成概念
2.未知数的指数是一次;
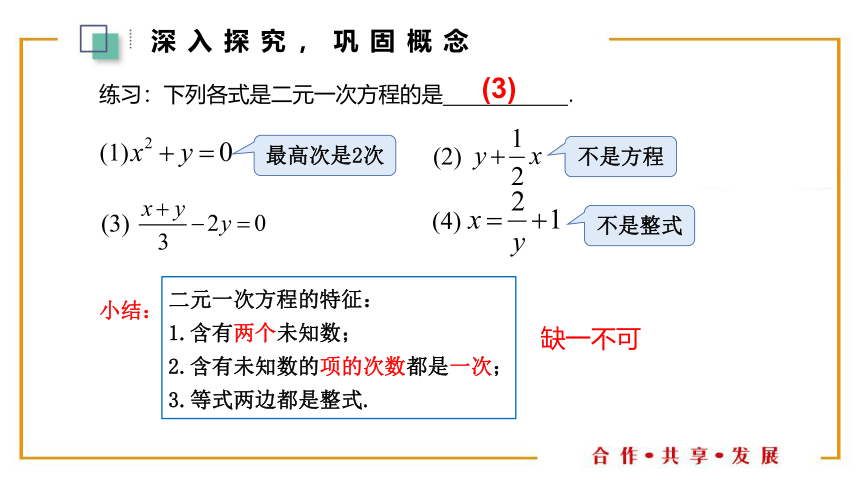
练习:下列各式是二元一次方程的是 .
(4)
(3)
(2)
(3)
小结:
二元一次方程的特征:
1.含有两个未知数;
2.含有未知数的项的次数都是一次;
3.等式两边都是整式.
缺一不可
(1)
最高次是2次
不是整式
不是方程
深入探究,巩固概念
当x=1时,y=14,所以该方程的解记做
回顾:什么是一元一次方程的解?
使一元一次方程两边的值相等的未知数的值叫做一元一次方程的解.
类比:什么是二元一次方程的解?
使二元一次方程两边的值相等的一对未知数的值,叫做二元一次方程的一个解.
例如:
x=1
y=14.
深入探究,形成概念
讨论:二元一次方程的解有几个?
如果不考虑方程表示的实际意义,还可以取哪些值?这些值是有限的吗?
二元一次方程有无数个解
练习:检验下列各组数是不是方程2a=3b+2的解
a=4
b=3
①
×
√
√
a=4
b=2
②
a=7
b=4
③
…
深入探究,形成概念
小结方法:把解带入方程,两边的值相等,则说明是方程的解.
例 已知方程3x+2y=10.
(1) 用关于x的代数式表示y.
(2) 求当x=-2 ,0, 3时,对应的y的值,并写出方程3x+2y=10的三个解.
分析:要用关于x的代数式表示y,只要把方程3x+2y=10看做未知数是y的一元一次方程.
解(1)移项,得2y=10-3x.
(2)当x=-2时,
当x=0时,
当x=3时,
;;
例题演练,掌握新知
方程变形步骤:
1、移项
2、两边同除以系数
变式:用y关于的代数式表示x.
比较一元一次方程和二元一次方程的相同点和不同点.
相同点:
不同点:
一元一次方程 二元一次方程
定义
方程的解
类比
含有一个未知数
含有两个未知数
只有一个解
一个未知数的值
有无数多个解
一对未知数的值,记做
x=
y=
转化
含有未知数的项的次数都是一次(方程两边都是整式).
课堂小结,梳理新知
课中作业,当堂检测
A组 基础练习
1.下列各式是二元一次方程的是( )
A. B. C. D.
D
2.下列各组数是方程的解有 .(填序号)
x=
y=0
①
x=-1.5
y=
②
x=
y=1
③
3.已知方程
(1)用含x的代数式表示y.
(2)用含y的代数式表示x.
①②
课中作业,当堂检测
B组 提升练习
4.48名同学被分配到大、小不同的两种寝室,大寝室每间住6人,小寝室每间住4人,刚好住满.求大、小寝室各住了多少间.如果设大寝室住了x间,小寝室住了y间,请列出方程,并写出所有的解.
x=4
y=6
x=6
y=3
x=2
y=9
5.若方程是关于x,y的二元一次方程,则a = .
变式:若方程是关于x,y的二元一次方程,则a = .
概念
解法
应用
单元整体,类比教学
生
长
数
学
学
生
命
成
长
1.请同学们回顾一下,我们已经学习了哪类方程?请举一个例子.
2.在学习这类方程时,我们学习了它的哪些相关知识?
3.请给你举的例子,加上情境,编成一道应用题.
课前作业,回顾旧知
概念
解法
应用
2.1 二元一次方程
根据题意列出方程:
(2)七年级二班男生人数的两倍比女生人数的三倍多七人,求男生、女生的人数.设男生人数为a,女生人数为b,则列出方程 .
问题引入,章节起始
(1)篮球联赛中,每场比赛都要分出胜负,每队胜一场得2分,负一场得1分,如果甲队在这次比赛中一共得了16分,求甲队在这次比赛中胜负各几场?设甲队胜x场,负y场,则列出方程 .
请你根据一元一次方程的特征,类比得出二元一次方程的概念.
一元一次方程
二元一次方程
1.含有一个未知数;
2.未知数的指数是一次;
3.等式两边都是整式.
2.含有未知数的项的次数都是一次;
二元一次方程的概念:
含有两个未知数,且含有未知数的项的次数都是一次的方程叫做二元一次方程.
类比思想
3.等式两边都是整式.
1.含有两个未知数;
深入探究,形成概念
2.未知数的指数是一次;
练习:下列各式是二元一次方程的是 .
(4)
(3)
(2)
(3)
小结:
二元一次方程的特征:
1.含有两个未知数;
2.含有未知数的项的次数都是一次;
3.等式两边都是整式.
缺一不可
(1)
最高次是2次
不是整式
不是方程
深入探究,巩固概念
当x=1时,y=14,所以该方程的解记做
回顾:什么是一元一次方程的解?
使一元一次方程两边的值相等的未知数的值叫做一元一次方程的解.
类比:什么是二元一次方程的解?
使二元一次方程两边的值相等的一对未知数的值,叫做二元一次方程的一个解.
例如:
x=1
y=14.
深入探究,形成概念
讨论:二元一次方程的解有几个?
如果不考虑方程表示的实际意义,还可以取哪些值?这些值是有限的吗?
二元一次方程有无数个解
练习:检验下列各组数是不是方程2a=3b+2的解
a=4
b=3
①
×
√
√
a=4
b=2
②
a=7
b=4
③
…
深入探究,形成概念
小结方法:把解带入方程,两边的值相等,则说明是方程的解.
例 已知方程3x+2y=10.
(1) 用关于x的代数式表示y.
(2) 求当x=-2 ,0, 3时,对应的y的值,并写出方程3x+2y=10的三个解.
分析:要用关于x的代数式表示y,只要把方程3x+2y=10看做未知数是y的一元一次方程.
解(1)移项,得2y=10-3x.
(2)当x=-2时,
当x=0时,
当x=3时,
;;
例题演练,掌握新知
方程变形步骤:
1、移项
2、两边同除以系数
变式:用y关于的代数式表示x.
比较一元一次方程和二元一次方程的相同点和不同点.
相同点:
不同点:
一元一次方程 二元一次方程
定义
方程的解
类比
含有一个未知数
含有两个未知数
只有一个解
一个未知数的值
有无数多个解
一对未知数的值,记做
x=
y=
转化
含有未知数的项的次数都是一次(方程两边都是整式).
课堂小结,梳理新知
课中作业,当堂检测
A组 基础练习
1.下列各式是二元一次方程的是( )
A. B. C. D.
D
2.下列各组数是方程的解有 .(填序号)
x=
y=0
①
x=-1.5
y=
②
x=
y=1
③
3.已知方程
(1)用含x的代数式表示y.
(2)用含y的代数式表示x.
①②
课中作业,当堂检测
B组 提升练习
4.48名同学被分配到大、小不同的两种寝室,大寝室每间住6人,小寝室每间住4人,刚好住满.求大、小寝室各住了多少间.如果设大寝室住了x间,小寝室住了y间,请列出方程,并写出所有的解.
x=4
y=6
x=6
y=3
x=2
y=9
5.若方程是关于x,y的二元一次方程,则a = .
变式:若方程是关于x,y的二元一次方程,则a = .
概念
解法
应用
单元整体,类比教学
生
长
数
学
学
生
命
成
长
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
