浙教版七年级下册 2.3 解二元一次方程组 课件(共19张PPT)
文档属性
| 名称 | 浙教版七年级下册 2.3 解二元一次方程组 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
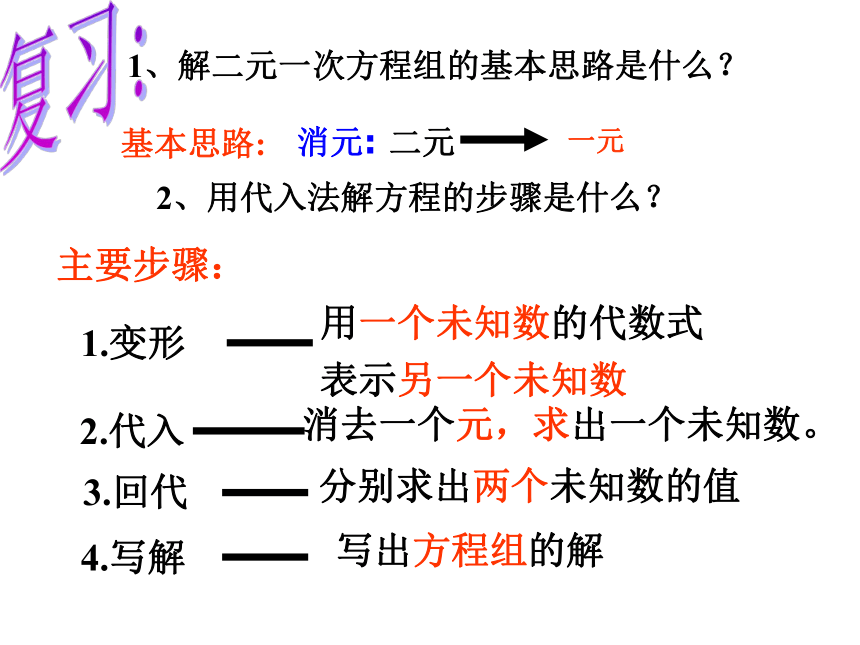
主要步骤:
基本思路:
4.写解
3.回代
2.代入
一元
分别求出两个未知数的值
写出方程组的解
1.变形
用一个未知数的代数式
表示另一个未知数
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
消去一个元,求出一个未知数。
消元: 二元
一元
怎样解下面的二元一次方程组呢?
①
②
把②变形得:
代入①,不就消去
了!
小明
①
②
把②变形得
可以直接代入①呀!
小彬
①
②
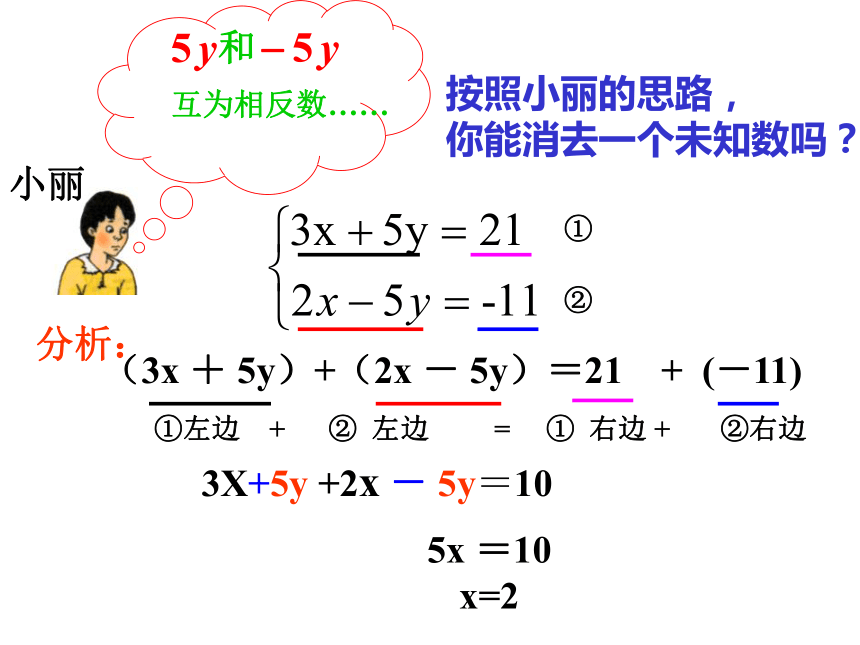
和
互为相反数……
按照小丽的思路,
你能消去一个未知数吗?
小丽
(3x + 5y)+(2x - 5y)=21 + (-11)
分析:
①
②
3X+5y +2x - 5y=10
①左边 + ② 左边 = ① 右边 + ②右边
5x =10
x=2
所以原方程组的解是
①
②
解:由①+②得: 5x=10
把x=2代入①,得
x=2
y=3
参考小丽的思路,
怎样解下面的二元一次方程组呢?
2x-5y=7 ①
2x+3y=-1 ②
观察方程组中的两个方程,未知数x的系数相等,都是2。把两个方程两边分别相减,就可以消去未知数x,同样得到一个一元一次方程。
分析
2x-5y=7 ①
2x+3y=-1 ②
解:把 ②-①得:8y=-8
y=-1
把y =-1代入①,得
2x-5×(-1)=7
解得:x=1
所以原方程组的解是
x=1
y=-1
指出下列方程组求解过程中有错误步骤,并给予订正:
7x-4y=4
5x-4y=-4
解:①-②,得
2x=4-4,
x=0
①
①
②
②
3x-4y=14
5x+4y=2
解 ①-②,得
-2x=12
x =-6
解: ①-②,得
2x=4+4,
x=4
解: ①+②,得
8x=16
x =2
上面这些方程组的特点是什么
解这类方程组基本思路是什么?
主要步骤有哪些?
特点:
基本思路:
主要步骤:
同一个未知数的系数相同或互为相反数
加减消元:
二元
一元
加减
消去一个元
求解
分别求出两个未知数的值
写解
写出方程组的解
A
试一试
7x-2y=3
9x+2y=-19
6x-5y=3
6x+y=-15
用加减消元法解下列方程组.(你可以选择你喜欢的一题解答)
①
②
①
②
例4. 解方程组:
①×3得
所以原方程组的解是
①
②
分析:
③-④得: y=2
把y =2代入①,
解得: x=3
②×2得
6x+9y=36 ③
6x+8y=34 ④
当方程组中两方程未知数系数不具备相同或互为相反数的特点时
要建立一个未知数系数的绝对值相等的,且与原方程组同解的新的方程组。
再用加减消元法解.
解:
用加减消元法解下列方程组.
(你可以选择你喜欢的一题解答)
练一练
4s+3t=5
2s-t=-5
5x-6y=9
7x-4y=-5
①
②
①
②
谈谈你对解二元一次方程组的认识
请同学们归纳一下:
什么样的方程组用“代入法”?
什么样的方程组用“加减法”?
二元一次方程
一元一次方程
消元
转化
加减
消去一个元
求解
分别求出两个未知数的值
变形
同一个未知数的系
数相同或互为相反数
写解
写出方程组的解
“加减消元法”主要步骤有哪些?
补 充1
补 充2
a1x+b1y=c1
a2x+b2y=c2
x=6
y=8
3a1x+2b1y=5c1
3a2x+2b2y=5c2
x=10
y=20
x=10
y=20
三个同学对问题“若方程组
的解是 ,
求方程组 的解.”
提出各自的想法.
甲说:“这个题目好象条件不够,不能求解”;
乙说:“它们的系数有一定的规律,可以试试”;
丙说:“能不能把第二个方程组的两个方程的
两边都除以5,通过换元替代的方法来解决”.
参考他们的讨论,你认为这个题目的解应该是 .
主要步骤:
基本思路:
4.写解
3.回代
2.代入
一元
分别求出两个未知数的值
写出方程组的解
1.变形
用一个未知数的代数式
表示另一个未知数
1、解二元一次方程组的基本思路是什么?
2、用代入法解方程的步骤是什么?
消去一个元,求出一个未知数。
消元: 二元
一元
怎样解下面的二元一次方程组呢?
①
②
把②变形得:
代入①,不就消去
了!
小明
①
②
把②变形得
可以直接代入①呀!
小彬
①
②
和
互为相反数……
按照小丽的思路,
你能消去一个未知数吗?
小丽
(3x + 5y)+(2x - 5y)=21 + (-11)
分析:
①
②
3X+5y +2x - 5y=10
①左边 + ② 左边 = ① 右边 + ②右边
5x =10
x=2
所以原方程组的解是
①
②
解:由①+②得: 5x=10
把x=2代入①,得
x=2
y=3
参考小丽的思路,
怎样解下面的二元一次方程组呢?
2x-5y=7 ①
2x+3y=-1 ②
观察方程组中的两个方程,未知数x的系数相等,都是2。把两个方程两边分别相减,就可以消去未知数x,同样得到一个一元一次方程。
分析
2x-5y=7 ①
2x+3y=-1 ②
解:把 ②-①得:8y=-8
y=-1
把y =-1代入①,得
2x-5×(-1)=7
解得:x=1
所以原方程组的解是
x=1
y=-1
指出下列方程组求解过程中有错误步骤,并给予订正:
7x-4y=4
5x-4y=-4
解:①-②,得
2x=4-4,
x=0
①
①
②
②
3x-4y=14
5x+4y=2
解 ①-②,得
-2x=12
x =-6
解: ①-②,得
2x=4+4,
x=4
解: ①+②,得
8x=16
x =2
上面这些方程组的特点是什么
解这类方程组基本思路是什么?
主要步骤有哪些?
特点:
基本思路:
主要步骤:
同一个未知数的系数相同或互为相反数
加减消元:
二元
一元
加减
消去一个元
求解
分别求出两个未知数的值
写解
写出方程组的解
A
试一试
7x-2y=3
9x+2y=-19
6x-5y=3
6x+y=-15
用加减消元法解下列方程组.(你可以选择你喜欢的一题解答)
①
②
①
②
例4. 解方程组:
①×3得
所以原方程组的解是
①
②
分析:
③-④得: y=2
把y =2代入①,
解得: x=3
②×2得
6x+9y=36 ③
6x+8y=34 ④
当方程组中两方程未知数系数不具备相同或互为相反数的特点时
要建立一个未知数系数的绝对值相等的,且与原方程组同解的新的方程组。
再用加减消元法解.
解:
用加减消元法解下列方程组.
(你可以选择你喜欢的一题解答)
练一练
4s+3t=5
2s-t=-5
5x-6y=9
7x-4y=-5
①
②
①
②
谈谈你对解二元一次方程组的认识
请同学们归纳一下:
什么样的方程组用“代入法”?
什么样的方程组用“加减法”?
二元一次方程
一元一次方程
消元
转化
加减
消去一个元
求解
分别求出两个未知数的值
变形
同一个未知数的系
数相同或互为相反数
写解
写出方程组的解
“加减消元法”主要步骤有哪些?
补 充1
补 充2
a1x+b1y=c1
a2x+b2y=c2
x=6
y=8
3a1x+2b1y=5c1
3a2x+2b2y=5c2
x=10
y=20
x=10
y=20
三个同学对问题“若方程组
的解是 ,
求方程组 的解.”
提出各自的想法.
甲说:“这个题目好象条件不够,不能求解”;
乙说:“它们的系数有一定的规律,可以试试”;
丙说:“能不能把第二个方程组的两个方程的
两边都除以5,通过换元替代的方法来解决”.
参考他们的讨论,你认为这个题目的解应该是 .
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
