浙教版七年级下册 1.3 平行线的判定 课件(共19张PPT)
文档属性
| 名称 | 浙教版七年级下册 1.3 平行线的判定 课件(共19张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 503.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-23 19:54:46 | ||
图片预览



文档简介
(共19张PPT)
浙教版七年级下册第1章平行线
1.了解平行线的判定方法:
“内错角相等,两直线平行”
“同旁内角互补,两直线平行”的产生过程;
2.掌握平行线的判定方法:
“内错角相等,两直线平行”
“同旁内角互补,两直线平行”;
3.会用“内错角相等,两直线平行”
“同旁内角互补,两直线平行”
判定两直线平行.会进行简单的推理及其表述.
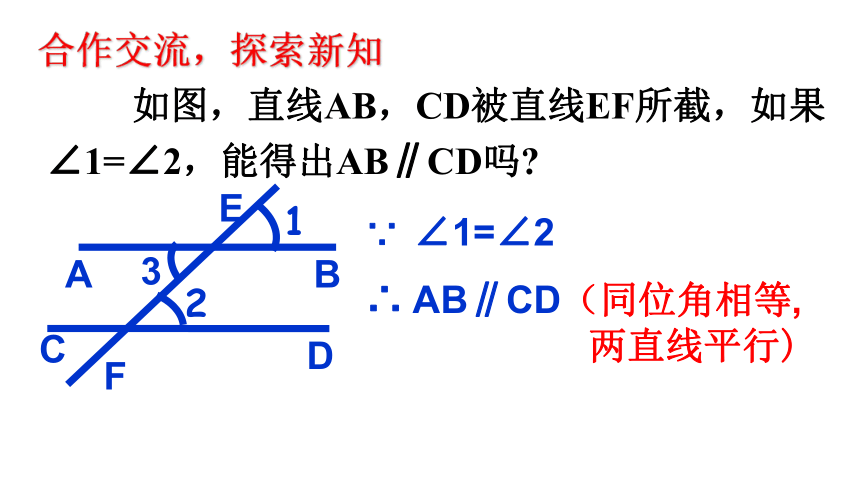
合作交流,探索新知
∵ ∠1=∠2
∴ AB∥CD(同位角相等,
两直线平行)
B
3
A
C
D
F
1
2
E
如图,直线AB,CD被直线EF所截,如果
∠1=∠2,能得出AB∥CD吗
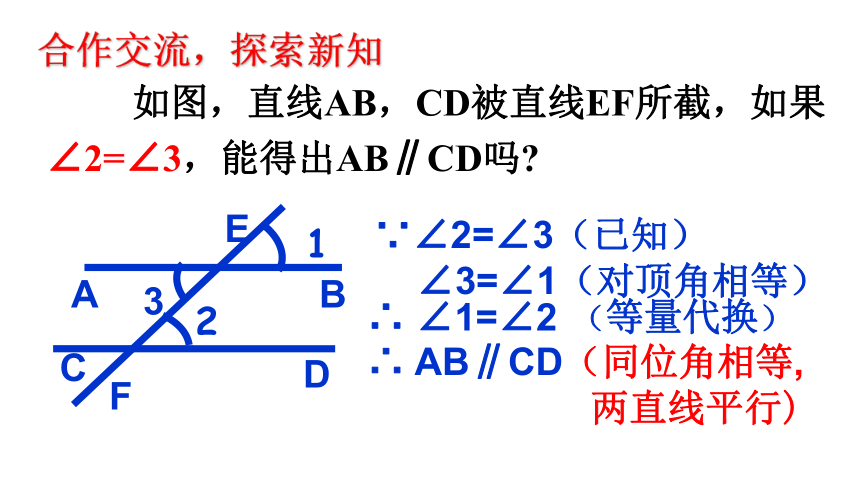
合作交流,探索新知
∵∠2=∠3(已知)
∠3=∠1(对顶角相等)
∴ ∠1=∠2
∴ AB∥CD(同位角相等,
两直线平行)
B
3
A
C
D
F
1
2
E
如图,直线AB,CD被直线EF所截,如果
∠2=∠3,能得出AB∥CD吗
(等量代换)
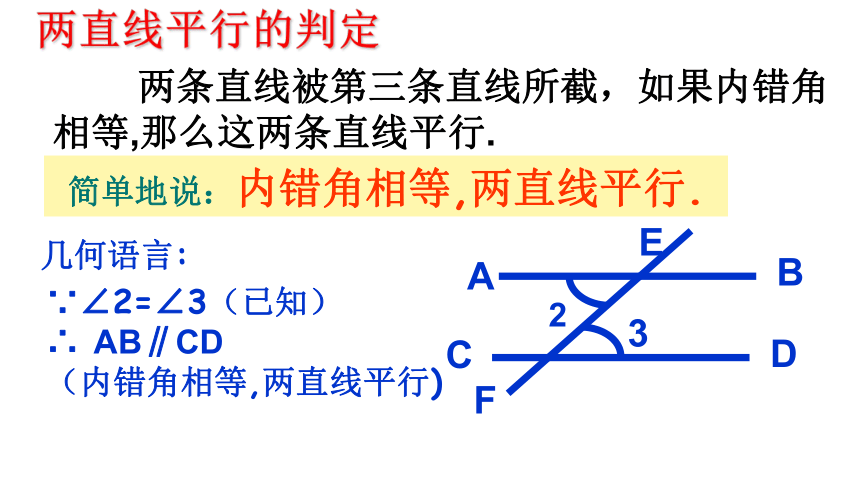
两直线平行的判定
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
B
2
3
A
D
E
F
C
∵∠2=∠3(已知)
∴ AB∥CD
(内错角相等,两直线平行)
几何语言:
简单地说:内错角相等,两直线平行.
1
2
3
l2
l1
l3
l4
1、如图,已知∠1=121°,∠2 =120°, ∠3=120°.说出其中的平行线,并说明理由.
尝试反馈,巩固练习
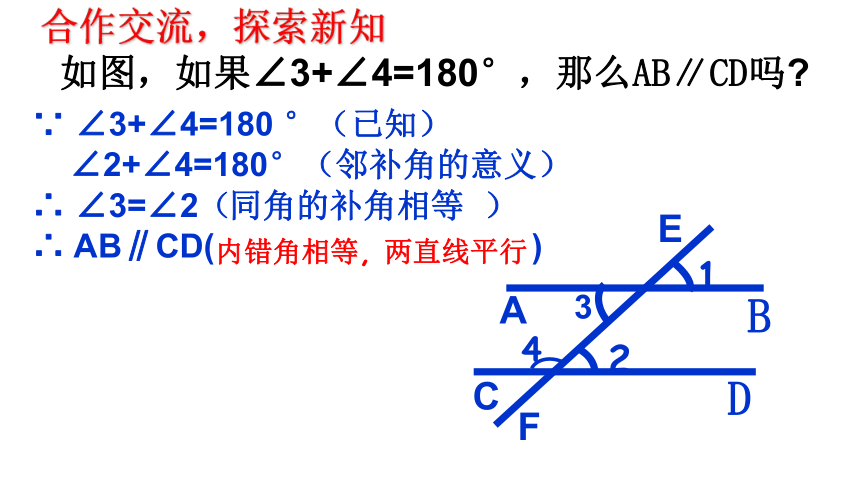
如图,如果∠3+∠4=180°,那么AB∥CD吗
∵ ∠3+∠4=180 °(已知)
∠2+∠4=180°(邻补角的意义)
∴ ∠3=∠2( )
∴ AB∥CD( )
3
2
A
C
1
D
B
E
F
4
同角的补角相等
内错角相等, 两直线平行
合作交流,探索新知
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
2
B
A
C
D
E
F
3
几何语言:
∵ ∠2+∠3=180 °(已知)
∴ AB∥CD(同旁内角互补, 两直线平行)
简单地说
同旁内角互补,两直线平行
两直线平行的判定
1.如图,直线AB 、CD被直线EF所截.
尝试反馈,巩固练习
(1)量得∠1=80°,∠3=100° , 则AB∥CD 根据什么?
(2)量得∠3=100°,∠4=100°,则AB∥CD 根据什么?
2.如图所示:
(1)由∠DCE =∠D,可判断哪两条直线平行?
(2)由∠1=∠2,可判断哪两条直线平行?
B
(1)AD//BE
(2)AB//DC
尝试反馈,巩固练习
1.同位角相等
2.内错角相等
3.同旁内角互补
两直线平行
平行条件
条件: 角的关系 平行关系
4.在同一平面内,垂直于同一条直线的两条直线
互相平行.
5.平行线的定义.
例3
如图,AC⊥CD于点C,∠1与∠2互余.
判断AB,CD是否平行,并说明理由.
A
B
C
D
1
2
3
E
如图, AP平分∠BAC, CP平分∠ACD , ∠1+∠2= 90O,判断AB与CD是否平行,
并说明理由.
A
B
C
D
P
1
2
例4
如图:∠C+∠A= ∠AEC,判断AB与CD是否平行,并说明理由;
A
B
C
D
E
F
分析:延长CE,交AB于点F,则直线CD,AB被直线CF所截。这样,我们可以通过判断内错角∠C和∠AFC是否相等,来判定AB与CD是否平行。
A
B
C
D
E
1、如图,∠C=∠E+ ∠A,判断AB与CD是否平行,并说明理由.
A
B
C
D
E
F
解:∵ ∠C=∠E+ ∠A (已知)
又∵ ∠E+∠A= ∠AFC
(三角形的外角等于与它不相邻的两个内角和 )
∴ ∠C= ∠AFC
∴AB//CD
(内错角相等,两直线平行)
变式一:
应用拓展
变式二:
如图,∠C+∠A+∠AEC=360°.判断AB与CD是否平行,并说明理由.
A
B
C
D
E
A
B
C
D
E
F
应用拓展
解题技巧:找截线,构造截线
基本图形
P
A
B
C
1
2
3
4
应用拓展
台球运动中,如果母球P击中桌边点A,经桌边反弹后击中相邻的另一条桌边,再次反弹,那么母球P经过的路线BC与PA平行吗?请说明你判断的理由.
能说出你这节课的收获和体验让大家与你分享吗?
布置作业
1、作业本1.3.2
2、课后练习
浙教版七年级下册第1章平行线
1.了解平行线的判定方法:
“内错角相等,两直线平行”
“同旁内角互补,两直线平行”的产生过程;
2.掌握平行线的判定方法:
“内错角相等,两直线平行”
“同旁内角互补,两直线平行”;
3.会用“内错角相等,两直线平行”
“同旁内角互补,两直线平行”
判定两直线平行.会进行简单的推理及其表述.
合作交流,探索新知
∵ ∠1=∠2
∴ AB∥CD(同位角相等,
两直线平行)
B
3
A
C
D
F
1
2
E
如图,直线AB,CD被直线EF所截,如果
∠1=∠2,能得出AB∥CD吗
合作交流,探索新知
∵∠2=∠3(已知)
∠3=∠1(对顶角相等)
∴ ∠1=∠2
∴ AB∥CD(同位角相等,
两直线平行)
B
3
A
C
D
F
1
2
E
如图,直线AB,CD被直线EF所截,如果
∠2=∠3,能得出AB∥CD吗
(等量代换)
两直线平行的判定
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
B
2
3
A
D
E
F
C
∵∠2=∠3(已知)
∴ AB∥CD
(内错角相等,两直线平行)
几何语言:
简单地说:内错角相等,两直线平行.
1
2
3
l2
l1
l3
l4
1、如图,已知∠1=121°,∠2 =120°, ∠3=120°.说出其中的平行线,并说明理由.
尝试反馈,巩固练习
如图,如果∠3+∠4=180°,那么AB∥CD吗
∵ ∠3+∠4=180 °(已知)
∠2+∠4=180°(邻补角的意义)
∴ ∠3=∠2( )
∴ AB∥CD( )
3
2
A
C
1
D
B
E
F
4
同角的补角相等
内错角相等, 两直线平行
合作交流,探索新知
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
2
B
A
C
D
E
F
3
几何语言:
∵ ∠2+∠3=180 °(已知)
∴ AB∥CD(同旁内角互补, 两直线平行)
简单地说
同旁内角互补,两直线平行
两直线平行的判定
1.如图,直线AB 、CD被直线EF所截.
尝试反馈,巩固练习
(1)量得∠1=80°,∠3=100° , 则AB∥CD 根据什么?
(2)量得∠3=100°,∠4=100°,则AB∥CD 根据什么?
2.如图所示:
(1)由∠DCE =∠D,可判断哪两条直线平行?
(2)由∠1=∠2,可判断哪两条直线平行?
B
(1)AD//BE
(2)AB//DC
尝试反馈,巩固练习
1.同位角相等
2.内错角相等
3.同旁内角互补
两直线平行
平行条件
条件: 角的关系 平行关系
4.在同一平面内,垂直于同一条直线的两条直线
互相平行.
5.平行线的定义.
例3
如图,AC⊥CD于点C,∠1与∠2互余.
判断AB,CD是否平行,并说明理由.
A
B
C
D
1
2
3
E
如图, AP平分∠BAC, CP平分∠ACD , ∠1+∠2= 90O,判断AB与CD是否平行,
并说明理由.
A
B
C
D
P
1
2
例4
如图:∠C+∠A= ∠AEC,判断AB与CD是否平行,并说明理由;
A
B
C
D
E
F
分析:延长CE,交AB于点F,则直线CD,AB被直线CF所截。这样,我们可以通过判断内错角∠C和∠AFC是否相等,来判定AB与CD是否平行。
A
B
C
D
E
1、如图,∠C=∠E+ ∠A,判断AB与CD是否平行,并说明理由.
A
B
C
D
E
F
解:∵ ∠C=∠E+ ∠A (已知)
又∵ ∠E+∠A= ∠AFC
(三角形的外角等于与它不相邻的两个内角和 )
∴ ∠C= ∠AFC
∴AB//CD
(内错角相等,两直线平行)
变式一:
应用拓展
变式二:
如图,∠C+∠A+∠AEC=360°.判断AB与CD是否平行,并说明理由.
A
B
C
D
E
A
B
C
D
E
F
应用拓展
解题技巧:找截线,构造截线
基本图形
P
A
B
C
1
2
3
4
应用拓展
台球运动中,如果母球P击中桌边点A,经桌边反弹后击中相邻的另一条桌边,再次反弹,那么母球P经过的路线BC与PA平行吗?请说明你判断的理由.
能说出你这节课的收获和体验让大家与你分享吗?
布置作业
1、作业本1.3.2
2、课后练习
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
