浙教版七年级下册 2.5 有理数的乘方 课件(共34张PPT)
文档属性
| 名称 | 浙教版七年级下册 2.5 有理数的乘方 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 16:55:04 | ||
图片预览








文档简介
(共34张PPT)
2.5 有理数的乘方(1)
如果你第一天给我1元,第二天给我2元,第三天给我4元,以此类推,一直给20天,我就让你享用!
每天给我10元,一共给20年。
我就不吃你!
灰太狼会答应喜羊羊的建议吗?
第1天: 1
第2天: 2
第3天: 4
=2×2
第4天: 8
第5天:16
……
第20天
=2 ×2 ×2
= 2 ×2 ×2 ×2
19个2
=2×2×······×2
10×365×20=
它能不能简化,该如何简化呢
相同因数的乘法
复习
问题一:
相同加数的加法如何简化?
6+6+6+6+6=
10+10+10=
(-2)+(-2) +(-2) +(-2)=
6×5
10×3
(-2)×4
新课
问题二:
相同因数的乘法如何简化?
6 + 6 + 6 + 6 + 6=
10 + 10 + 10=
(-2) + (-2) + (-2) + (-2)=
×
×
×
×
×
×
×
×
×
5
5
5
5
5
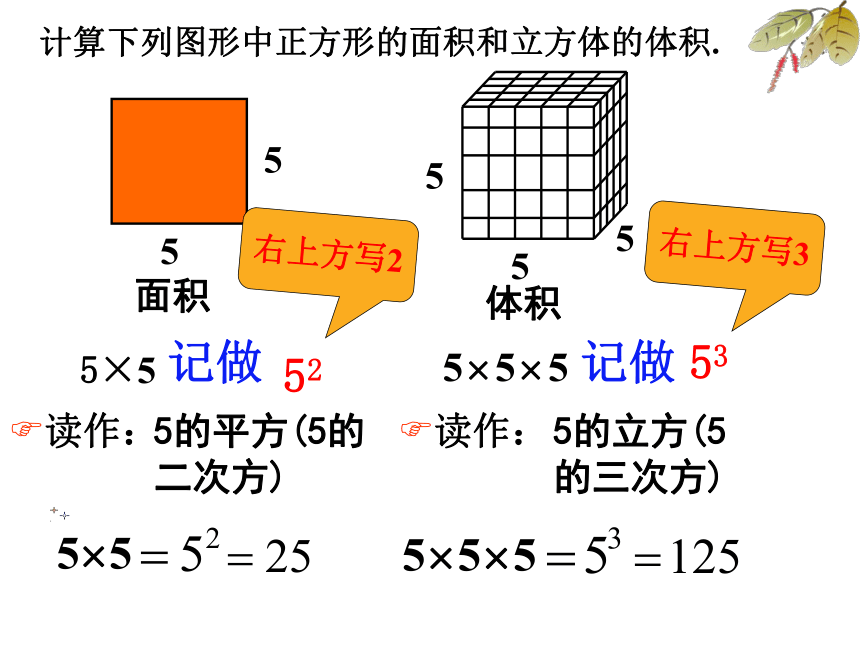
5的平方(5的二次方)
5的立方(5的三次方)
面积
体积
计算下列图形中正方形的面积和立方体的体积.
5×5
记做
52
记做
53
读作:
读作:
右上方写3
右上方写2
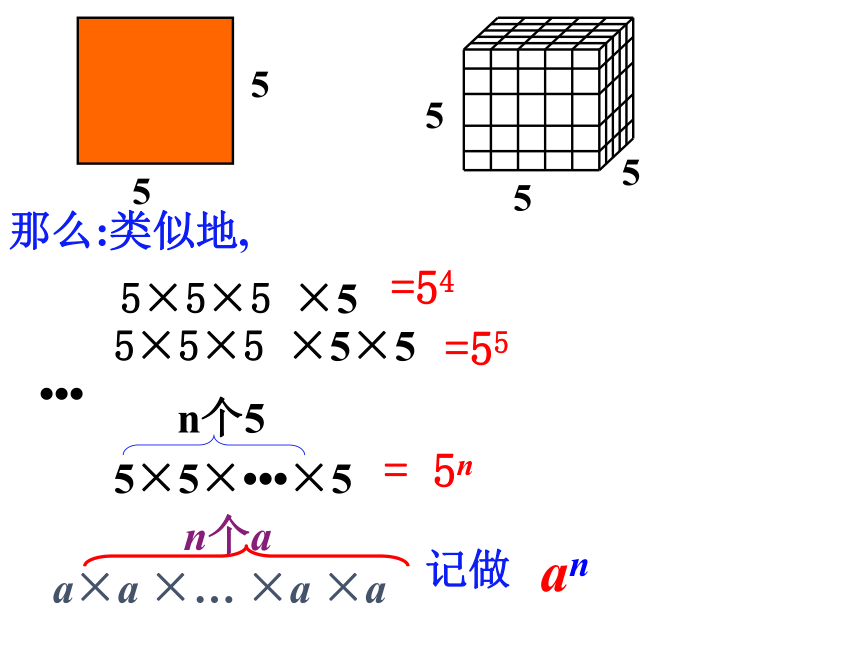
那么:类似地,
5×5×5 ×5
5×5×5 ×5×5
5×5× ×5
n个5
=54
=55
= 5n
5
5
5
5
5
a×a ×… ×a ×a
n个a
记做
an
an
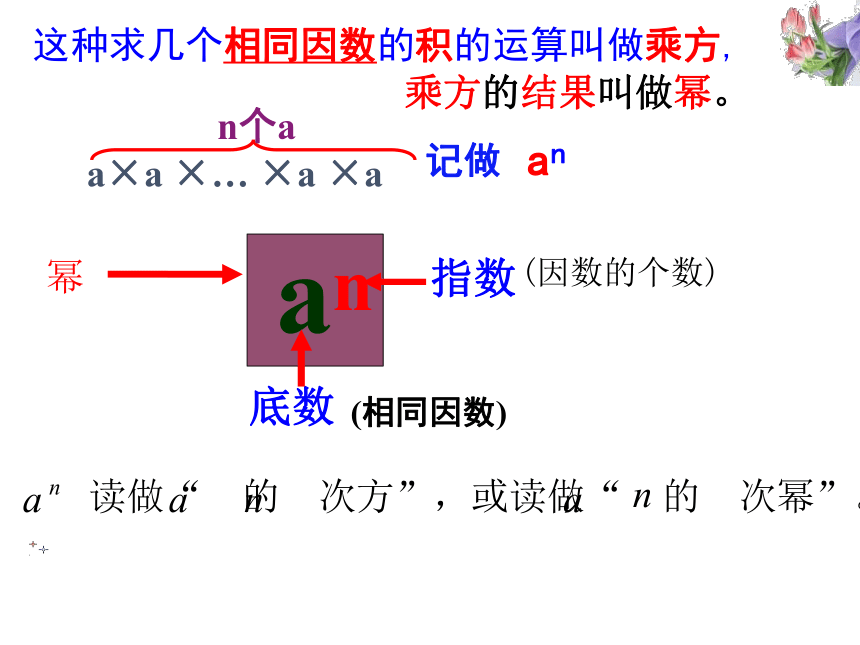
乘方的结果叫做幂。
读做“ 的 次方”,或读做“ 的 次幂”。
幂
指数
(因数的个数)
底数
(相同因数)
这种求几个相同因数的积的运算叫做乘方,
a×a ×… ×a ×a
n个a
记做
an
学习了乘方的概念之后,下列各式该如何简化?
6x6x6x6x6=
10x10x10x10x10=
(-2)x(-2) x(-2)
x(-2)x(-2) x(-2)=
65
105
(-2)6
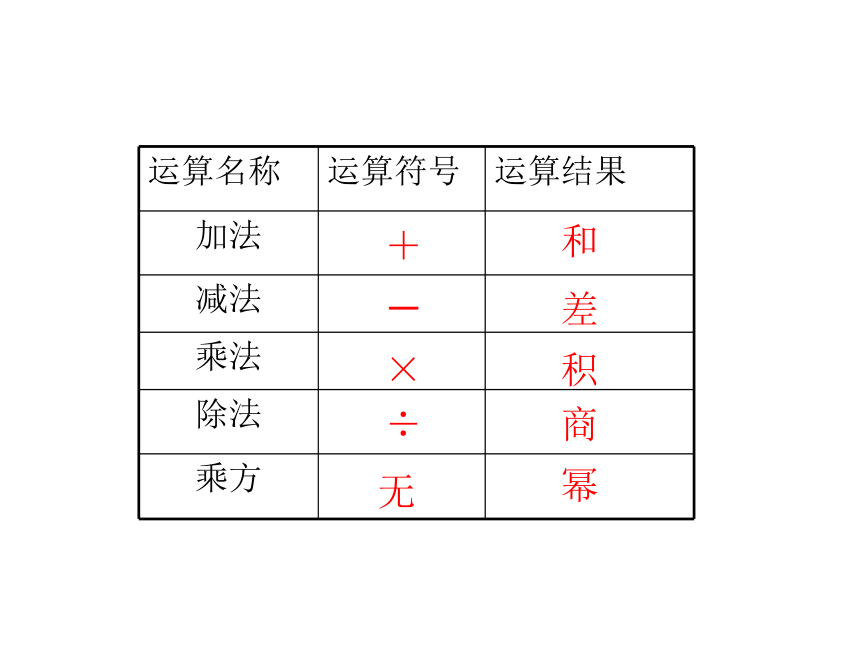
运算名称 运算符号 运算结果
加法
减法
乘法
除法
乘方
+
-
差
和
积
×
÷
商
幂
无
9
4
9
9的4次方
9的4次幂
1、在 中,底数是_________,指数是__________,
表示4个____相乘,读作___________,也读作____________.
2、 的底数是______,指数是________,表示____________,
读作_____的2次方,也读作-5的__________.
-5
2
2个-5相乘
-5
2次幂
3、 表示______个 相乘,叫做 的______次方,也叫
做 的_____次幂,其中, 叫做_______,4叫做_______.
4
4
4
底数
指数
轻松过关
4、把(-6)×(-6) ×(-6) 写成幂的形式是 ,
5、把 × × × 写成幂的形式
是 ,;
(-6)3
2
3
2
3
2
3
2
3
幂的底数是负数或分数时,底数应该添上括号
轻松过关
轻松过关
6. 的底数是_______,指数是_________,读作___________
0
8
0的8次方
7. 6的底数是__________,指数是__________.
6
1
一个数可以看作这个数的本身的一次方。
思考:说说下列各数的意义,它们一样吗
思考:说说下列各数的意义,它们一样吗
例1 计算:
(1)(-3)2 (2) 1.53
解:(1) (-3)2 =
(-3)× (-3)
=9;
(2) 1.53
=1.5 × 1.5 × 1.5
=3.375;
(4) (-1)11
= -1
(3)
算一算
规律:
1、负数的偶次幂是正数
2、负数的奇次幂是负数
3、正数的任何次幂都是正数。
4、 0的任何次幂都是0
5、 1的任何次幂都为1,-1的偶次幂是1,
-1的1奇次幂是-1.
幂的性质:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。
口答
1、 是 (填“正”或“负”)数;
2、 是 (填“正”或“负”)数;
3、 是 (填“正”或“负”)数;
4、 是 (填“正”或“负”)数;
正
负
正
负
解:(1)原式=-(3×3)=-9
(2)原式=3×8=24
(4)原式=8÷(-8)=-1
对于有理数的混合运算,应先算乘方,再算乘除;最后算加减,如果遇到括号,就先进行括号里的运算.
有理数运算序
例2 计算
(1) -32 (2)3x23 (3) (3x2)3
(4)8÷(-2)3
计算:
(1)8×23; (2)(5×2)3;
(3)(-2)2×(-3)2;
(4)(-2)3÷22.
解:(1)8×23=8×8=64;(2)(5×2)3=103=1000;
(3)(-2)2×(-3)2=4× 9=36;
(4)(-2)3÷22 =(-8)÷4=-2.
变式训练
第1天: 1
第2天: 2
第3天: 4
=2×2
第4天: 8
第5天: 16
……
第20天
=2 ×2 ×2
= 2 ×2 ×2 ×2
19个2
=2×2×······×2
=22
=23
=24
=219
学以致用
喜羊羊的学问
1048575元
73000元
10×365×20=
某种传染病一人感染后一小时内传染给两人,以后他没有再传染别人。而那两人同样在一小时内每人又分别传染另外的两人。如此下去,一昼夜能传染一个百万人口的市区吗?
请注意,一小时内,一个人只传染两个人,一昼夜只有24小时,一个百万人口的市区能都传染吗?
能?还是不能?
猜一猜
2
2×2
2×2×2
第1个小时,传染2人;
第2个小时,传染2×2人 即4人;
第3个小时,传染23人, 即8人;
第4个小时,传染24人, 即16人;
… …
第23个小时,传染223人,即8388608人;
第24个小时,传染224人,即16777216人。
分析:
每天只需要多出一点点的努力,365天之后将积累成巨大的力量 ,相反每天稍稍的偷下懒,365天后将会比以前更差!
积跬步以至千里,
积懈怠以致深渊.
感悟
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
8分题
12分题
8分题
10分题
挑战自我
小结
A. 4个5相乘 B. 5个4相乘
C. 5与4的积 D. 5个4相加的和
选一选
(2). 计算 (-1)100 + ( -1)101 的值是( )
A. 1100 B. -1 C. 0 D. -1100
B
C
(每题4分)
(1). 45 表示 ( )
填一填:
(1). 6的平方是____, -6的平方是____.
(2).比较大小(填入“>”“<”或“=”):
36
36
① 34____43 ② -0.1___ -0.13
<
>
(每空格2分)
(1) 5×23
(每题5分)
算一算:
(2) (-2)3÷22
下列运算对吗 如不对,请改正.
×
火眼金睛
( )
⑴
( )
⑵
×
8
6
(每题3分)
( )
×
(3)
( )
(-2)3= 8
-8
×
本节课你学到了什么
1.有理数的乘方的意义和相关概念。
2.乘方的有关运算。
3.体会特殊到一般,具体到抽象的数学方法。
幂的底数是分数或负数时,底数应该添上括号.
作业
作业本
2.5 有理数的乘方(1)
如果你第一天给我1元,第二天给我2元,第三天给我4元,以此类推,一直给20天,我就让你享用!
每天给我10元,一共给20年。
我就不吃你!
灰太狼会答应喜羊羊的建议吗?
第1天: 1
第2天: 2
第3天: 4
=2×2
第4天: 8
第5天:16
……
第20天
=2 ×2 ×2
= 2 ×2 ×2 ×2
19个2
=2×2×······×2
10×365×20=
它能不能简化,该如何简化呢
相同因数的乘法
复习
问题一:
相同加数的加法如何简化?
6+6+6+6+6=
10+10+10=
(-2)+(-2) +(-2) +(-2)=
6×5
10×3
(-2)×4
新课
问题二:
相同因数的乘法如何简化?
6 + 6 + 6 + 6 + 6=
10 + 10 + 10=
(-2) + (-2) + (-2) + (-2)=
×
×
×
×
×
×
×
×
×
5
5
5
5
5
5的平方(5的二次方)
5的立方(5的三次方)
面积
体积
计算下列图形中正方形的面积和立方体的体积.
5×5
记做
52
记做
53
读作:
读作:
右上方写3
右上方写2
那么:类似地,
5×5×5 ×5
5×5×5 ×5×5
5×5× ×5
n个5
=54
=55
= 5n
5
5
5
5
5
a×a ×… ×a ×a
n个a
记做
an
an
乘方的结果叫做幂。
读做“ 的 次方”,或读做“ 的 次幂”。
幂
指数
(因数的个数)
底数
(相同因数)
这种求几个相同因数的积的运算叫做乘方,
a×a ×… ×a ×a
n个a
记做
an
学习了乘方的概念之后,下列各式该如何简化?
6x6x6x6x6=
10x10x10x10x10=
(-2)x(-2) x(-2)
x(-2)x(-2) x(-2)=
65
105
(-2)6
运算名称 运算符号 运算结果
加法
减法
乘法
除法
乘方
+
-
差
和
积
×
÷
商
幂
无
9
4
9
9的4次方
9的4次幂
1、在 中,底数是_________,指数是__________,
表示4个____相乘,读作___________,也读作____________.
2、 的底数是______,指数是________,表示____________,
读作_____的2次方,也读作-5的__________.
-5
2
2个-5相乘
-5
2次幂
3、 表示______个 相乘,叫做 的______次方,也叫
做 的_____次幂,其中, 叫做_______,4叫做_______.
4
4
4
底数
指数
轻松过关
4、把(-6)×(-6) ×(-6) 写成幂的形式是 ,
5、把 × × × 写成幂的形式
是 ,;
(-6)3
2
3
2
3
2
3
2
3
幂的底数是负数或分数时,底数应该添上括号
轻松过关
轻松过关
6. 的底数是_______,指数是_________,读作___________
0
8
0的8次方
7. 6的底数是__________,指数是__________.
6
1
一个数可以看作这个数的本身的一次方。
思考:说说下列各数的意义,它们一样吗
思考:说说下列各数的意义,它们一样吗
例1 计算:
(1)(-3)2 (2) 1.53
解:(1) (-3)2 =
(-3)× (-3)
=9;
(2) 1.53
=1.5 × 1.5 × 1.5
=3.375;
(4) (-1)11
= -1
(3)
算一算
规律:
1、负数的偶次幂是正数
2、负数的奇次幂是负数
3、正数的任何次幂都是正数。
4、 0的任何次幂都是0
5、 1的任何次幂都为1,-1的偶次幂是1,
-1的1奇次幂是-1.
幂的性质:正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正数。
口答
1、 是 (填“正”或“负”)数;
2、 是 (填“正”或“负”)数;
3、 是 (填“正”或“负”)数;
4、 是 (填“正”或“负”)数;
正
负
正
负
解:(1)原式=-(3×3)=-9
(2)原式=3×8=24
(4)原式=8÷(-8)=-1
对于有理数的混合运算,应先算乘方,再算乘除;最后算加减,如果遇到括号,就先进行括号里的运算.
有理数运算序
例2 计算
(1) -32 (2)3x23 (3) (3x2)3
(4)8÷(-2)3
计算:
(1)8×23; (2)(5×2)3;
(3)(-2)2×(-3)2;
(4)(-2)3÷22.
解:(1)8×23=8×8=64;(2)(5×2)3=103=1000;
(3)(-2)2×(-3)2=4× 9=36;
(4)(-2)3÷22 =(-8)÷4=-2.
变式训练
第1天: 1
第2天: 2
第3天: 4
=2×2
第4天: 8
第5天: 16
……
第20天
=2 ×2 ×2
= 2 ×2 ×2 ×2
19个2
=2×2×······×2
=22
=23
=24
=219
学以致用
喜羊羊的学问
1048575元
73000元
10×365×20=
某种传染病一人感染后一小时内传染给两人,以后他没有再传染别人。而那两人同样在一小时内每人又分别传染另外的两人。如此下去,一昼夜能传染一个百万人口的市区吗?
请注意,一小时内,一个人只传染两个人,一昼夜只有24小时,一个百万人口的市区能都传染吗?
能?还是不能?
猜一猜
2
2×2
2×2×2
第1个小时,传染2人;
第2个小时,传染2×2人 即4人;
第3个小时,传染23人, 即8人;
第4个小时,传染24人, 即16人;
… …
第23个小时,传染223人,即8388608人;
第24个小时,传染224人,即16777216人。
分析:
每天只需要多出一点点的努力,365天之后将积累成巨大的力量 ,相反每天稍稍的偷下懒,365天后将会比以前更差!
积跬步以至千里,
积懈怠以致深渊.
感悟
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
8分题
12分题
8分题
10分题
挑战自我
小结
A. 4个5相乘 B. 5个4相乘
C. 5与4的积 D. 5个4相加的和
选一选
(2). 计算 (-1)100 + ( -1)101 的值是( )
A. 1100 B. -1 C. 0 D. -1100
B
C
(每题4分)
(1). 45 表示 ( )
填一填:
(1). 6的平方是____, -6的平方是____.
(2).比较大小(填入“>”“<”或“=”):
36
36
① 34____43 ② -0.1___ -0.13
<
>
(每空格2分)
(1) 5×23
(每题5分)
算一算:
(2) (-2)3÷22
下列运算对吗 如不对,请改正.
×
火眼金睛
( )
⑴
( )
⑵
×
8
6
(每题3分)
( )
×
(3)
( )
(-2)3= 8
-8
×
本节课你学到了什么
1.有理数的乘方的意义和相关概念。
2.乘方的有关运算。
3.体会特殊到一般,具体到抽象的数学方法。
幂的底数是分数或负数时,底数应该添上括号.
作业
作业本
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
