2022—2023学年浙教版数学七年级下册 第四章 因式分解 复习课件(共17张PPT)
文档属性
| 名称 | 2022—2023学年浙教版数学七年级下册 第四章 因式分解 复习课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 189.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-30 00:00:00 | ||
图片预览


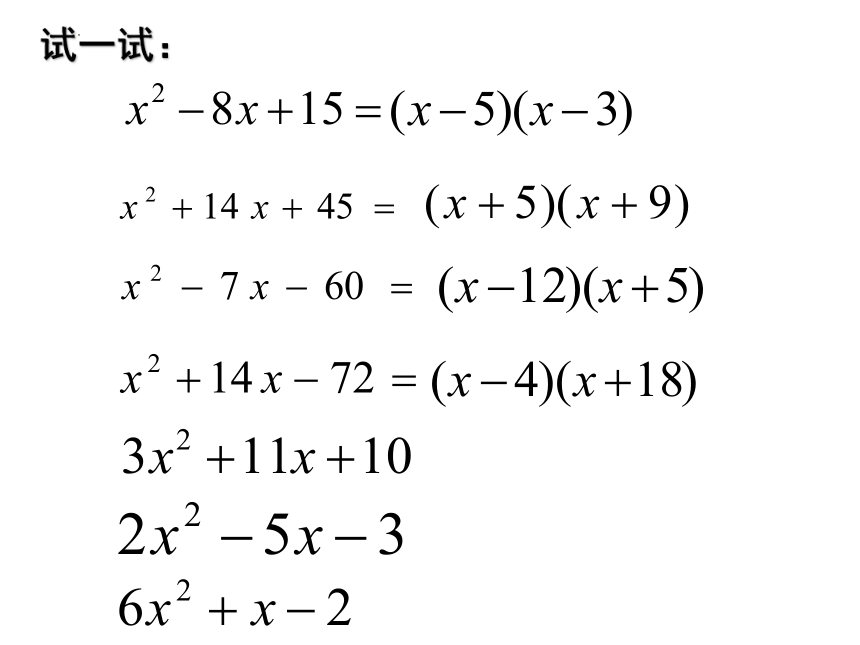




文档简介
(共17张PPT)
第四章因式分解复习
因式分解的基本方法:
因式分解的相关概念:
提取公因式法:
公式法:
把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式分解因式.
十字相乘法:
试一试:
1、下列等式从左边到右边的变形,
属于因式分解的是:( )
D
因式分解
整式乘法
a2-b2
(a-b)(a+b)
因式分解与整式乘法有什么关系
互逆
3、下列变形正确的是: ( )
B
4.
填空:填上适当的代数式,使之成为完全平方式
叫做完全平方式。
叫做完全平方式。
10或-6
因式分解的一般步骤:
第一步:先看多项式各项有无公因式,
如有公因式则要先提取公因式;
第二步:再看有几项,
如两项,则考虑用平方差公式;
如三项,则考虑用完全平方公式;
第三步:最后看各因式能否再分解,
如能分解,应分解到不能再分解为止。
因式分解的结果:一、最简;二、彻底。
2、计算:25 × 2652-1352 × 25
拓展提高:
1、分解因式:
3、求(2+1)(22+1)(24+1)……(232+1)+1的个位数字;
4、若248-1能被60与70之间的两个整数整除,这两个整数分别是 与 ;
5、已知,x+ y =7,x-y =5,求代数式 x 2- y2-2y+2x的值.
6、若n是整数,证明(2n+1)2-(2n-1)2是8的倍数.
11
7、已知x2+ax-12能分解成两个
整系数的一次因式的乘积,则
符合条件的整数a的个数是
( )
A、3个 B、4个
C、6个 D、8个
2.因式分解的一般思路:
一提(提公因式法)
二用(运用公式法)
1.因式分解方法:
(1) 提取公因式法
平方差公式法 (两项)
完全平方公式法(三项)
(2) 公式法
13
◆创新应用:
已知(a+2b)2-2a-4b+1=0,
求(a+2b)2005的值.
拓展提高
14
(1)已知a,b为自然数,
且a2 –b2 =45,
那么a= ,b= 。
提高题:
2、
第四章因式分解复习
因式分解的基本方法:
因式分解的相关概念:
提取公因式法:
公式法:
把一个多项式化成几个整式积的形式,这种变形叫做把这个多项式分解因式.
十字相乘法:
试一试:
1、下列等式从左边到右边的变形,
属于因式分解的是:( )
D
因式分解
整式乘法
a2-b2
(a-b)(a+b)
因式分解与整式乘法有什么关系
互逆
3、下列变形正确的是: ( )
B
4.
填空:填上适当的代数式,使之成为完全平方式
叫做完全平方式。
叫做完全平方式。
10或-6
因式分解的一般步骤:
第一步:先看多项式各项有无公因式,
如有公因式则要先提取公因式;
第二步:再看有几项,
如两项,则考虑用平方差公式;
如三项,则考虑用完全平方公式;
第三步:最后看各因式能否再分解,
如能分解,应分解到不能再分解为止。
因式分解的结果:一、最简;二、彻底。
2、计算:25 × 2652-1352 × 25
拓展提高:
1、分解因式:
3、求(2+1)(22+1)(24+1)……(232+1)+1的个位数字;
4、若248-1能被60与70之间的两个整数整除,这两个整数分别是 与 ;
5、已知,x+ y =7,x-y =5,求代数式 x 2- y2-2y+2x的值.
6、若n是整数,证明(2n+1)2-(2n-1)2是8的倍数.
11
7、已知x2+ax-12能分解成两个
整系数的一次因式的乘积,则
符合条件的整数a的个数是
( )
A、3个 B、4个
C、6个 D、8个
2.因式分解的一般思路:
一提(提公因式法)
二用(运用公式法)
1.因式分解方法:
(1) 提取公因式法
平方差公式法 (两项)
完全平方公式法(三项)
(2) 公式法
13
◆创新应用:
已知(a+2b)2-2a-4b+1=0,
求(a+2b)2005的值.
拓展提高
14
(1)已知a,b为自然数,
且a2 –b2 =45,
那么a= ,b= 。
提高题:
2、
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
