浙教版七年级下册 1.3 平行线的判定 课件 共14张
文档属性
| 名称 | 浙教版七年级下册 1.3 平行线的判定 课件 共14张 |

|
|
| 格式 | pptx | ||
| 文件大小 | 758.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-03 00:00:00 | ||
图片预览




文档简介
(共14张PPT)
1.3 平行线的判定(2)
引入新知
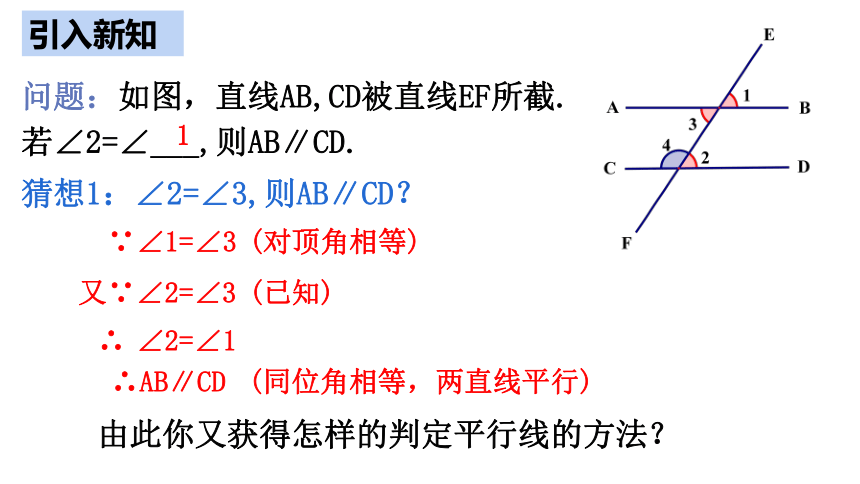
问题:如图,直线AB,CD被直线EF所截.
∵∠2=∠1
∴AB∥CD
(同位角相等,两直线平行)
若∠2=∠___,则AB∥CD.
1
猜想1:∠2=∠3,则AB∥CD?
∵∠1=∠3
(对顶角相等)
又∵∠2=∠3
(已知)
∴
由此你又获得怎样的判定平行线的方法?
探索新知
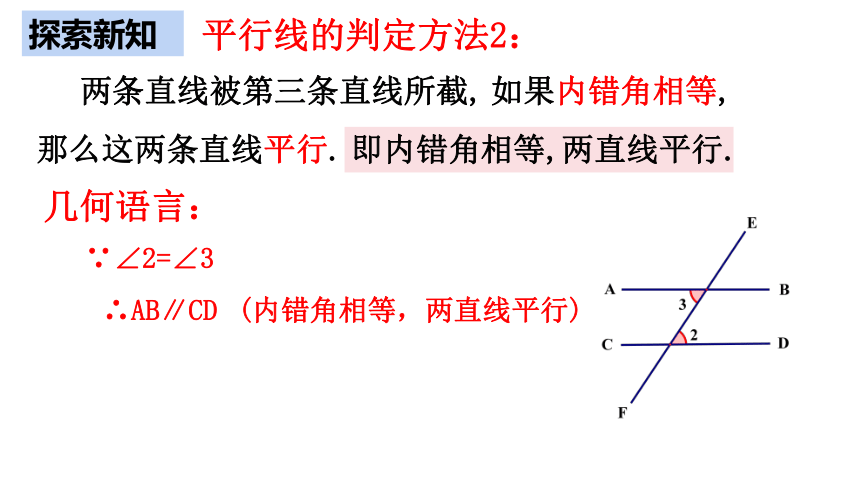
平行线的判定方法2:
两条直线被第三条直线所截,
如果内错角相等,
那么这两条直线平行.
即内错角相等,两直线平行.
几何语言:
∵∠2=∠3
∴AB∥CD
(内错角相等,两直线平行)
3
1
2
探索新知
如图,已知
写出其中的平行线,并说明理由.
解:l3∥l4
∵∠2=∠3=120°
∴l3∥l4
(内错角相等,两直线平行)
(课本P12做一做)
A
B
C
D
2
3
1
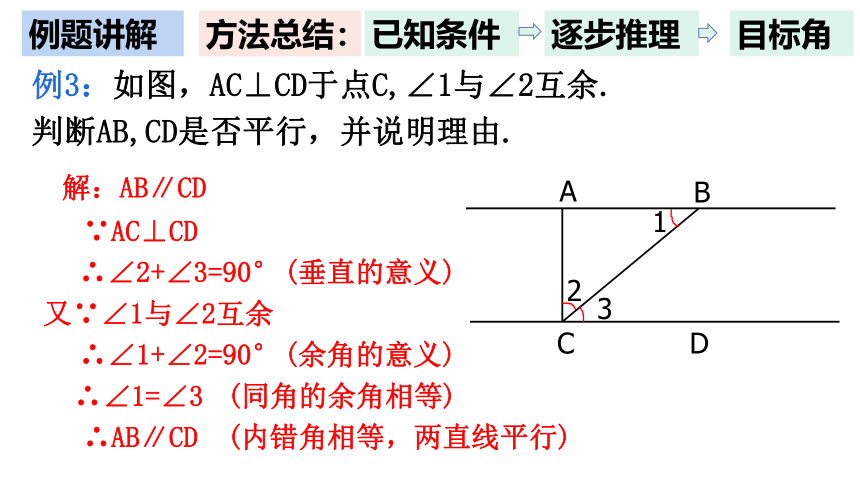
例3:如图,AC⊥CD于点C,∠1与∠2互余.
判断AB,CD是否平行,并说明理由.
例题讲解
解:AB∥CD
∵AC⊥CD
∴∠2+∠3=90°
又∵∠1与∠2互余
∴∠1+∠2=90°
∴∠1=∠3
∴AB∥CD
(垂直的意义)
(余角的意义)
(同角的余角相等)
(内错角相等,两直线平行)
方法总结:
目标角
已知条件
逐步推理
阶段小结 我们已经有哪几种判定两直线平行的方法?
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角 ,两直线平行.
猜想2:∠3+∠4=180°,则AB∥CD?
∵∠3+∠4=180°
又∵∠2+∠4=180°
∴∠2=∠3
∴AB∥CD
(已知)
(平角的意义)
(同角的补角相等)
(内错角相等,两直线平行)
互补
几何语言:
(同旁内角互补,两直线平行)
例题讲解
例4:如图,AP平分∠BAC,CP平分∠ACD,
∠1+∠2=90°,判断AB,CD是否平行.
解:AB∥CD
∵AP平分∠BAC,CP平分∠ACD
∴∠BAC=2∠1,∠ACD=2∠2
∴∠BAC+∠ACD=2∠1+2∠2
=2(∠1+∠2)=2×90°=180°
∴AB∥CD
(角平分线的意义)
(同旁内角互补,两直线平行)
方法总结:
已知条件
目标角
逐步推理
练习1:电子屏幕上显示的数字“9”的形状如图,根据图形填空:
( )
( )
( )
( )
( )
F
E
D
C
B
A
3
2
1
5
4
已知
已知
AB
EF
BC
ED
AB
CD
巩固练习
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
(课本P13作业题第2题)
练习2 如图, 已知直线l1,l2被直线l3所截,∠1+∠2=180°.请说明l1与l2平行的理由.
解 ∵∠1+∠2=180°
又∵ ∠2=∠3
∴∠1+∠3=180°
∴ l1∥l2(同旁内角互补,两直线平行)
4
5
3
巩固练习
(课本P13课内练习第3题)
练习3: 如图,∠DAC=2∠C,AE平分∠DAC,
判断AE,BC是否平行,并说明理由.
巩固练习
(课本P14作业题第3题)
四.
∵∠C+∠2=90°
∠1=∠C
∴∠1+∠2=90°
∴ DE∥BC(同旁内角互补,两直线平行)
∵DE⊥BE
∴∠E=90°
∴∠E+∠EBC=∠E+∠1+∠2=90°+90°=180°
解 DE∥BC,理由如下:
巩固练习
练习4:如图DE⊥EB于点E,∠1=∠C,∠2与∠C互为余角.判断DE与BC是否平行,并说明理由.
(课本P14作业题第4题)
五.
拓展提高
探究活动:有一条纸带如图所示,如果工具只有圆规,怎样检验纸带的两条边沿是否平行?请说出你的方法和依据。
方法总结:
圆规可以测量角是否相等;
折叠可以得到直角.
感悟提升
六.
两直线平行
同位角相等
性质
内错角相等
同旁内角互补
对顶角
角平分线
垂直
互余(补)
在同一平面内,垂直于同一条直线的
练习2:如图∠1=59°,∠2=120°,∠3=120°,
∠4=121° 。说出其中的平行线,并说明理由。
E
F
G
A
B
C
D
1
3
2
H
4
巩固练习
1.3 平行线的判定(2)
引入新知
问题:如图,直线AB,CD被直线EF所截.
∵∠2=∠1
∴AB∥CD
(同位角相等,两直线平行)
若∠2=∠___,则AB∥CD.
1
猜想1:∠2=∠3,则AB∥CD?
∵∠1=∠3
(对顶角相等)
又∵∠2=∠3
(已知)
∴
由此你又获得怎样的判定平行线的方法?
探索新知
平行线的判定方法2:
两条直线被第三条直线所截,
如果内错角相等,
那么这两条直线平行.
即内错角相等,两直线平行.
几何语言:
∵∠2=∠3
∴AB∥CD
(内错角相等,两直线平行)
3
1
2
探索新知
如图,已知
写出其中的平行线,并说明理由.
解:l3∥l4
∵∠2=∠3=120°
∴l3∥l4
(内错角相等,两直线平行)
(课本P12做一做)
A
B
C
D
2
3
1
例3:如图,AC⊥CD于点C,∠1与∠2互余.
判断AB,CD是否平行,并说明理由.
例题讲解
解:AB∥CD
∵AC⊥CD
∴∠2+∠3=90°
又∵∠1与∠2互余
∴∠1+∠2=90°
∴∠1=∠3
∴AB∥CD
(垂直的意义)
(余角的意义)
(同角的余角相等)
(内错角相等,两直线平行)
方法总结:
目标角
已知条件
逐步推理
阶段小结 我们已经有哪几种判定两直线平行的方法?
同位角相等,两直线平行.
内错角相等,两直线平行.
同旁内角 ,两直线平行.
猜想2:∠3+∠4=180°,则AB∥CD?
∵∠3+∠4=180°
又∵∠2+∠4=180°
∴∠2=∠3
∴AB∥CD
(已知)
(平角的意义)
(同角的补角相等)
(内错角相等,两直线平行)
互补
几何语言:
(同旁内角互补,两直线平行)
例题讲解
例4:如图,AP平分∠BAC,CP平分∠ACD,
∠1+∠2=90°,判断AB,CD是否平行.
解:AB∥CD
∵AP平分∠BAC,CP平分∠ACD
∴∠BAC=2∠1,∠ACD=2∠2
∴∠BAC+∠ACD=2∠1+2∠2
=2(∠1+∠2)=2×90°=180°
∴AB∥CD
(角平分线的意义)
(同旁内角互补,两直线平行)
方法总结:
已知条件
目标角
逐步推理
练习1:电子屏幕上显示的数字“9”的形状如图,根据图形填空:
( )
( )
( )
( )
( )
F
E
D
C
B
A
3
2
1
5
4
已知
已知
AB
EF
BC
ED
AB
CD
巩固练习
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
(课本P13作业题第2题)
练习2 如图, 已知直线l1,l2被直线l3所截,∠1+∠2=180°.请说明l1与l2平行的理由.
解 ∵∠1+∠2=180°
又∵ ∠2=∠3
∴∠1+∠3=180°
∴ l1∥l2(同旁内角互补,两直线平行)
4
5
3
巩固练习
(课本P13课内练习第3题)
练习3: 如图,∠DAC=2∠C,AE平分∠DAC,
判断AE,BC是否平行,并说明理由.
巩固练习
(课本P14作业题第3题)
四.
∵∠C+∠2=90°
∠1=∠C
∴∠1+∠2=90°
∴ DE∥BC(同旁内角互补,两直线平行)
∵DE⊥BE
∴∠E=90°
∴∠E+∠EBC=∠E+∠1+∠2=90°+90°=180°
解 DE∥BC,理由如下:
巩固练习
练习4:如图DE⊥EB于点E,∠1=∠C,∠2与∠C互为余角.判断DE与BC是否平行,并说明理由.
(课本P14作业题第4题)
五.
拓展提高
探究活动:有一条纸带如图所示,如果工具只有圆规,怎样检验纸带的两条边沿是否平行?请说出你的方法和依据。
方法总结:
圆规可以测量角是否相等;
折叠可以得到直角.
感悟提升
六.
两直线平行
同位角相等
性质
内错角相等
同旁内角互补
对顶角
角平分线
垂直
互余(补)
在同一平面内,垂直于同一条直线的
练习2:如图∠1=59°,∠2=120°,∠3=120°,
∠4=121° 。说出其中的平行线,并说明理由。
E
F
G
A
B
C
D
1
3
2
H
4
巩固练习
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
