浙教版七年级下册 1.3.2 平行线的判定 课件 共17张
文档属性
| 名称 | 浙教版七年级下册 1.3.2 平行线的判定 课件 共17张 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-03 18:46:19 | ||
图片预览




文档简介
(共17张PPT)
浙教版义务教育教科书 七年级下册
1.3平行线的判定(2)
教学目标与重难点
1.了解平行线的判定方法:“内错角相等,两直线平行”“同旁内角互补,两直线平行”的产生过程.
2.掌握平行线的判定方法:“内错角相等,两直线平行”“同旁内角互补,两直线平行”.
3.会用“内错角相等,两直线平行”“同旁内角互补,两直线平行”判定两直线平行.会进行推理和简单的表述.
教学目标:
重点:本节教学的重点是平行线的判定方法“内错角相等,两直线平行”.
难点:例4有一定难度,是本节教学的难点.
1.3平行线的判定(1)
新知探究
1.3平行线的判定(2)
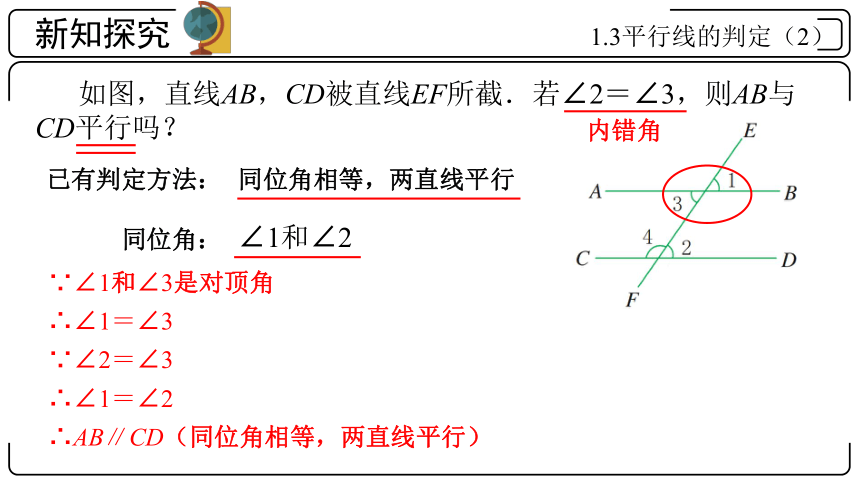
如图,直线AB,CD被直线EF所截.若∠2=∠3,则AB与CD平行吗?
已有判定方法:
同位角:
同位角相等,两直线平行
∠1和∠2
∵∠1和∠3是对顶角
∴∠1=∠3
∵∠2=∠3
∴∠1=∠2
∴AB∥CD(同位角相等,两直线平行)
内错角
新知探究
1.3平行线的判定(2)
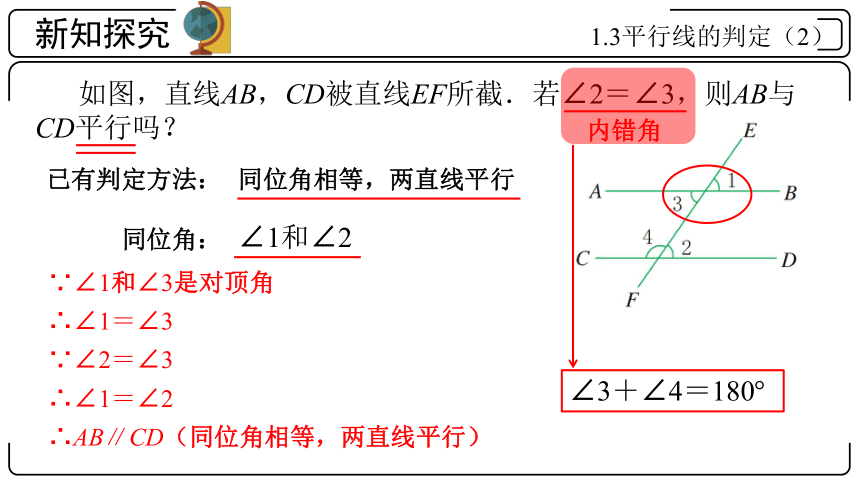
如图,直线AB,CD被直线EF所截.若∠2=∠3,则AB与CD平行吗?
已有判定方法:
同位角:
同位角相等,两直线平行
∠1和∠2
∵∠1和∠3是对顶角
∴∠1=∠3
∵∠2=∠3
∴∠1=∠2
∴AB∥CD(同位角相等,两直线平行)
内错角
∠3+∠4=180°
新知探究
1.3平行线的判定(2)
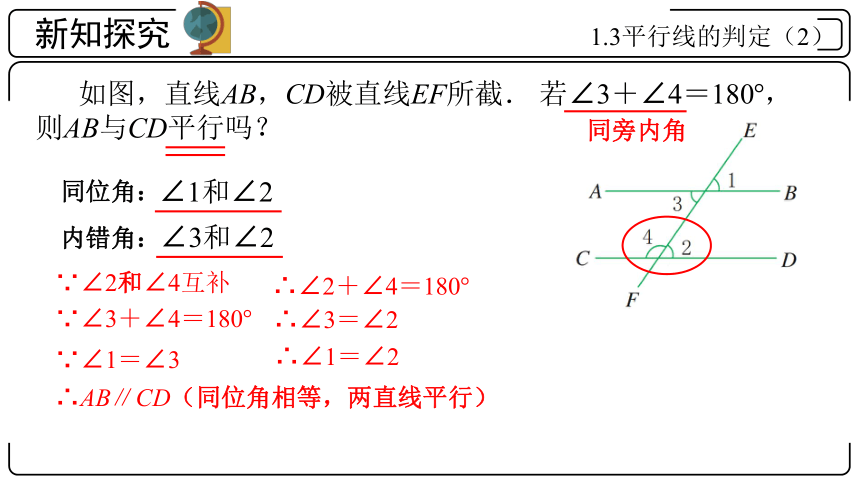
如图,直线AB,CD被直线EF所截. 若∠3+∠4=180°,则AB与CD平行吗?
内错角:
∠3和∠2
∵∠2和∠4互补
∴∠2+∠4=180°
∵∠3+∠4=180°
∴∠3=∠2
∴AB∥CD(同位角相等,两直线平行)
同旁内角
同位角:
∠1和∠2
∵∠1=∠3
∴∠1=∠2
新知探究
1.3平行线的判定(2)
两条直线被第三条直线所截,如果内错角相等,那么两直线平行.
内错角相等,两直线平行
几何语言:
∵∠2=∠3
∴AB∥CD
两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行.
同旁内角互补,两直线平行
∵∠3+∠4=180°
∴AB∥CD
当堂演练
1.3平行线的判定(2)
如图, 已知∠1=121°,∠2=120°, ∠3=120°. 说出
其中的平行线,并说明理由.
∵∠2=∠3=120°
∴l3∥l4(内错角相等,两直线平行)
当堂演练
1.3平行线的判定(2)
如图,已知直线l1,l2被直线 l3 所截,∠1+∠2=180°.请说明 l1 与 l2平行的理由.
∵∠2和∠3是对顶角
∴∠2=∠3
3
∵∠1+∠2=180°
∴∠1+∠3=180°
∴l1∥l2(同旁内角互补,两直线平行)
例题解析
例 如图,AC⊥CD 于点 C,∠1与∠2互余.判断 AB,CD 是否平行,并说明理由.
1.3平行线的判定(2)
∠2与∠3 互余
∠1与∠2 互余
∠1=∠3
内错角
内错角相等,两直线平行
AB∥CD
例题解析
例 如图,AC⊥CD 于点 C,∠1与∠2互余.判断 AB,CD 是否平行,并说明理由.
1.3平行线的判定(2)
解
AB∥CD,理由如下:
∵AC⊥CD
∴∠2+∠3=90°
∴AB∥CD(内错角相等,两直线平行)
∵∠1与∠2互余
∴∠1+∠2=90°
∴∠1=∠3(同角的余角相等)
当堂演练
练 如图,∠DAC=2∠C,AE平分∠DAC. 判断AE与BC是否平行,并说明理由.
1.3平行线的判定(2)
∠DAC=2∠EAC
∠EAC=∠C
当堂演练
练 如图,∠DAC=2∠C,AE平分∠DAC. 判断AE与BC是否平行,并说明理由.
解
AE∥BC.理由如下:
∵AE平分∠DAC
∴∠DAC=2∠EAC
∵∠DAC=2∠C
∴∠EAC=∠ACB
1.3平行线的判定(2)
∴AE∥BC(内错角相等,两直线平行)
例题解析
例 如图 ,AP 平分∠BAC,CP 平分∠ACD,∠1+∠2=90°.
判断 AB,CD是否平行,并说明理由.
1.3平行线的判定(2)
∠BAC=2∠1
∠DCA=2∠2
∠BAC+∠DCA=180°
同旁内角
同旁内角互补,两直线平行
AB∥CD
例题解析
例 如图 ,AP 平分∠BAC,CP 平分∠ACD,∠1+∠2=90°.判断 AB,CD是否平行,并说明理由.
1.3平行线的判定(2)
解
AB∥CD.理由如下:
∵AP平分∠BAC
∴∠BAC=2∠1
∴AB∥CD(同旁内角互补,两直线平行)
同理,∠DCA=2∠2
∵∠1+∠2=90°
∴∠BAC+∠DCA=180°
当堂演练
练 如图,DE⊥EB 于点 E,∠1=∠C,∠2 与∠C互为余角.
判断DE与BC是否平行,并说明理由.
1.3平行线的判定(2)
∠E=90°
∠2+∠C=90°
∠2+∠1=90°
∠E+∠EBC=180°
同旁内角
同旁内角互补,两直线平行
当堂演练
练 如图,DE⊥EB 于点 E,∠1=∠C,∠2 与∠C互为余角. 判断DE与BC是否平行,并说明理由.
1.3平行线的判定(2)
解
DE∥BC.理由如下:
∵DE⊥EB
∴∠E=90°
∵∠2与∠C互余
∴∠2+∠C=90°
∴DE∥BC(同旁内角互补,两直线平行)
∵∠1=∠C
∴∠1+∠2=90°
∴∠E+∠EBC=180°
课堂小结
内错角相等,两直线平行
简单说明“两直线平行”
1.3平行线的判定(2)
同位角相等,两直线平行
同旁内角互补,两直线平行
浙教版义务教育教科书 七年级下册
1.3平行线的判定(2)
教学目标与重难点
1.了解平行线的判定方法:“内错角相等,两直线平行”“同旁内角互补,两直线平行”的产生过程.
2.掌握平行线的判定方法:“内错角相等,两直线平行”“同旁内角互补,两直线平行”.
3.会用“内错角相等,两直线平行”“同旁内角互补,两直线平行”判定两直线平行.会进行推理和简单的表述.
教学目标:
重点:本节教学的重点是平行线的判定方法“内错角相等,两直线平行”.
难点:例4有一定难度,是本节教学的难点.
1.3平行线的判定(1)
新知探究
1.3平行线的判定(2)
如图,直线AB,CD被直线EF所截.若∠2=∠3,则AB与CD平行吗?
已有判定方法:
同位角:
同位角相等,两直线平行
∠1和∠2
∵∠1和∠3是对顶角
∴∠1=∠3
∵∠2=∠3
∴∠1=∠2
∴AB∥CD(同位角相等,两直线平行)
内错角
新知探究
1.3平行线的判定(2)
如图,直线AB,CD被直线EF所截.若∠2=∠3,则AB与CD平行吗?
已有判定方法:
同位角:
同位角相等,两直线平行
∠1和∠2
∵∠1和∠3是对顶角
∴∠1=∠3
∵∠2=∠3
∴∠1=∠2
∴AB∥CD(同位角相等,两直线平行)
内错角
∠3+∠4=180°
新知探究
1.3平行线的判定(2)
如图,直线AB,CD被直线EF所截. 若∠3+∠4=180°,则AB与CD平行吗?
内错角:
∠3和∠2
∵∠2和∠4互补
∴∠2+∠4=180°
∵∠3+∠4=180°
∴∠3=∠2
∴AB∥CD(同位角相等,两直线平行)
同旁内角
同位角:
∠1和∠2
∵∠1=∠3
∴∠1=∠2
新知探究
1.3平行线的判定(2)
两条直线被第三条直线所截,如果内错角相等,那么两直线平行.
内错角相等,两直线平行
几何语言:
∵∠2=∠3
∴AB∥CD
两条直线被第三条直线所截,如果同旁内角互补,那么两直线平行.
同旁内角互补,两直线平行
∵∠3+∠4=180°
∴AB∥CD
当堂演练
1.3平行线的判定(2)
如图, 已知∠1=121°,∠2=120°, ∠3=120°. 说出
其中的平行线,并说明理由.
∵∠2=∠3=120°
∴l3∥l4(内错角相等,两直线平行)
当堂演练
1.3平行线的判定(2)
如图,已知直线l1,l2被直线 l3 所截,∠1+∠2=180°.请说明 l1 与 l2平行的理由.
∵∠2和∠3是对顶角
∴∠2=∠3
3
∵∠1+∠2=180°
∴∠1+∠3=180°
∴l1∥l2(同旁内角互补,两直线平行)
例题解析
例 如图,AC⊥CD 于点 C,∠1与∠2互余.判断 AB,CD 是否平行,并说明理由.
1.3平行线的判定(2)
∠2与∠3 互余
∠1与∠2 互余
∠1=∠3
内错角
内错角相等,两直线平行
AB∥CD
例题解析
例 如图,AC⊥CD 于点 C,∠1与∠2互余.判断 AB,CD 是否平行,并说明理由.
1.3平行线的判定(2)
解
AB∥CD,理由如下:
∵AC⊥CD
∴∠2+∠3=90°
∴AB∥CD(内错角相等,两直线平行)
∵∠1与∠2互余
∴∠1+∠2=90°
∴∠1=∠3(同角的余角相等)
当堂演练
练 如图,∠DAC=2∠C,AE平分∠DAC. 判断AE与BC是否平行,并说明理由.
1.3平行线的判定(2)
∠DAC=2∠EAC
∠EAC=∠C
当堂演练
练 如图,∠DAC=2∠C,AE平分∠DAC. 判断AE与BC是否平行,并说明理由.
解
AE∥BC.理由如下:
∵AE平分∠DAC
∴∠DAC=2∠EAC
∵∠DAC=2∠C
∴∠EAC=∠ACB
1.3平行线的判定(2)
∴AE∥BC(内错角相等,两直线平行)
例题解析
例 如图 ,AP 平分∠BAC,CP 平分∠ACD,∠1+∠2=90°.
判断 AB,CD是否平行,并说明理由.
1.3平行线的判定(2)
∠BAC=2∠1
∠DCA=2∠2
∠BAC+∠DCA=180°
同旁内角
同旁内角互补,两直线平行
AB∥CD
例题解析
例 如图 ,AP 平分∠BAC,CP 平分∠ACD,∠1+∠2=90°.判断 AB,CD是否平行,并说明理由.
1.3平行线的判定(2)
解
AB∥CD.理由如下:
∵AP平分∠BAC
∴∠BAC=2∠1
∴AB∥CD(同旁内角互补,两直线平行)
同理,∠DCA=2∠2
∵∠1+∠2=90°
∴∠BAC+∠DCA=180°
当堂演练
练 如图,DE⊥EB 于点 E,∠1=∠C,∠2 与∠C互为余角.
判断DE与BC是否平行,并说明理由.
1.3平行线的判定(2)
∠E=90°
∠2+∠C=90°
∠2+∠1=90°
∠E+∠EBC=180°
同旁内角
同旁内角互补,两直线平行
当堂演练
练 如图,DE⊥EB 于点 E,∠1=∠C,∠2 与∠C互为余角. 判断DE与BC是否平行,并说明理由.
1.3平行线的判定(2)
解
DE∥BC.理由如下:
∵DE⊥EB
∴∠E=90°
∵∠2与∠C互余
∴∠2+∠C=90°
∴DE∥BC(同旁内角互补,两直线平行)
∵∠1=∠C
∴∠1+∠2=90°
∴∠E+∠EBC=180°
课堂小结
内错角相等,两直线平行
简单说明“两直线平行”
1.3平行线的判定(2)
同位角相等,两直线平行
同旁内角互补,两直线平行
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
