浙教版七年级下册 2.2 二元一次方程组 课件 共14张
文档属性
| 名称 | 浙教版七年级下册 2.2 二元一次方程组 课件 共14张 |
|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-03 18:51:57 | ||
图片预览





文档简介
(共14张PPT)
浙教版义务教育教科书 七年级下册
2.1二元一次方程组
教学目标与重难点
1.了解二元一次方程组的概念.
2.理解二元一次方程组的解的概念.
3.会用列表尝试的方法求解二元一次方程组的解.
教学目标:
重点:本节教学的重点是二元一次方程组及其解的概念.
难点:用列表尝试的方法求解二元一次方程组的解是本节教学的难点.
复习回顾
1.下列属于二元一次方程的是 ( )
A. B.
C. D.
2.方程2x+3y=8的解 ( )
A.只有一个 B.只有两个 C.只有三个 D.有无数个
A
D
新课引入
“鸡兔同笼,上有九头,下有二十八足,问鸡兔几何?”
思考:试着用一元一次方程来解这道题
解:设鸡的数量为x只,则兔的数量是(9-x)只.
2x+4(9-x)=28
x=4
答:鸡的数量为4只,则兔的数量是5只.
新课引入
“鸡兔同笼,上有九头,下有二十八足,问鸡兔几何?”
分析:设鸡有x只,兔有y只.
由“上有九头”可得x+y=9
问题①:这里列的是什么方程?列了几个?
由“下有二十八足”可得2x+4y=28
两个二元一次方程
问题②:两个方程里的未知数x和y有什么关系?
x和y都分别表示同一个未知数,
即 x和y的值需要同时满足上述两个方程
新知探究
二元一次方程组
由两个一次方程组成,并且含有两个未知数的方程组叫做二元一次方程组.
请判断下列各方程组中,哪些是二元一次方程组,哪些不是?并说明理由.
×
×
新知探究
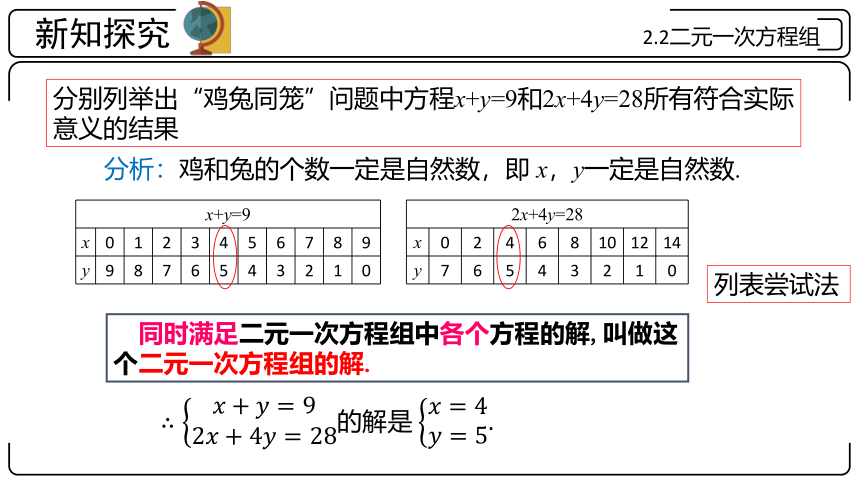
分别列举出“鸡兔同笼”问题中方程x+y=9和2x+4y=28所有符合实际意义的结果
分析:鸡和兔的个数一定是自然数,即 x,y一定是自然数.
x+y=9 x 0 1 2 3 4 5 6 7 8 9
y 9 8 7 6 5 4 3 2 1 0
2x+4y=28 x 0 2 4 6 8 10 12 14
y 7 6 5 4 3 2 1 0
同时满足二元一次方程组中各个方程的解,叫做这个二元一次方程组的解.
列表尝试法
当堂演练
1.把下列各组数的题序填入图中适当的位置:
方程x+y=0的解
方程2x+3y=2的解
①
②
③
④
x+y=0
2x+3y=2
方程组
的解
④
①
③
②
②
②
当堂演练
2.下面哪个解是二元一次方程组 的解 ( )
(A)
(B)
(C)
(D)
B
例题学习
2.2二元一次方程组
例 北京2008年奥运会跳水决赛的门票价格如下表:
小聪购买了B等级和C等级的跳水决赛门票共6张,他发现购买这6张门票所花的钱恰好能购买3张A等级门票,如果设小聪购买B等级和C等级门票分别是x张和y张,请根据问题中的条件列出关于x,y的方程组,并用列表尝试的方法求两种门票的数量。
等级 A B C
票价(元/张) 500 300 150
问1:情境中哪些是已知,哪些是未知的?
问2:情境中哪些语句能帮助你得到数量关系?
解:根据条件可列出关于x,y的方程组
x
y
300x+150y
0
1
2
3
4
5
6
6
5
4
3
2
1
0
900
1050
1200
1350
1500
1650
1800
思考:表格中x的值你会取哪些数?为什么?
可见,只有x=4,y=2 符合这个方程组,所以方程组的解是
x=4
y=2
答:小聪买了B等级跳水决赛门票4张,C等级跳水决赛门票2张.
例题学习
2.2二元一次方程组
课堂小结
二元一次方程组
概念
解
如何求解
注:二元一次方程组并不要求每个方程都是二元的.
列表尝试法
同时满足二元一次方程组中各个方程的解,叫做这个二元一次方程组的解.
课堂小结
一元一次方程的解 二元一次方程的解 二元一次方程组的解
个数
解的形式
1个
无数个
1个
一个未知数的值
一对未知数的值
一对未知数的值
思考:是不是所有二元一次方程组都有唯一解呢?
课后思考
“鸡兔同笼,上有九头,下有二十八足,问鸡兔几何?”
思考:明明用一元一次方程就能又快又简单地解得最终答案,为什么要用二元一次方程组来解决问题呢?
浙教版义务教育教科书 七年级下册
2.1二元一次方程组
教学目标与重难点
1.了解二元一次方程组的概念.
2.理解二元一次方程组的解的概念.
3.会用列表尝试的方法求解二元一次方程组的解.
教学目标:
重点:本节教学的重点是二元一次方程组及其解的概念.
难点:用列表尝试的方法求解二元一次方程组的解是本节教学的难点.
复习回顾
1.下列属于二元一次方程的是 ( )
A. B.
C. D.
2.方程2x+3y=8的解 ( )
A.只有一个 B.只有两个 C.只有三个 D.有无数个
A
D
新课引入
“鸡兔同笼,上有九头,下有二十八足,问鸡兔几何?”
思考:试着用一元一次方程来解这道题
解:设鸡的数量为x只,则兔的数量是(9-x)只.
2x+4(9-x)=28
x=4
答:鸡的数量为4只,则兔的数量是5只.
新课引入
“鸡兔同笼,上有九头,下有二十八足,问鸡兔几何?”
分析:设鸡有x只,兔有y只.
由“上有九头”可得x+y=9
问题①:这里列的是什么方程?列了几个?
由“下有二十八足”可得2x+4y=28
两个二元一次方程
问题②:两个方程里的未知数x和y有什么关系?
x和y都分别表示同一个未知数,
即 x和y的值需要同时满足上述两个方程
新知探究
二元一次方程组
由两个一次方程组成,并且含有两个未知数的方程组叫做二元一次方程组.
请判断下列各方程组中,哪些是二元一次方程组,哪些不是?并说明理由.
×
×
新知探究
分别列举出“鸡兔同笼”问题中方程x+y=9和2x+4y=28所有符合实际意义的结果
分析:鸡和兔的个数一定是自然数,即 x,y一定是自然数.
x+y=9 x 0 1 2 3 4 5 6 7 8 9
y 9 8 7 6 5 4 3 2 1 0
2x+4y=28 x 0 2 4 6 8 10 12 14
y 7 6 5 4 3 2 1 0
同时满足二元一次方程组中各个方程的解,叫做这个二元一次方程组的解.
列表尝试法
当堂演练
1.把下列各组数的题序填入图中适当的位置:
方程x+y=0的解
方程2x+3y=2的解
①
②
③
④
x+y=0
2x+3y=2
方程组
的解
④
①
③
②
②
②
当堂演练
2.下面哪个解是二元一次方程组 的解 ( )
(A)
(B)
(C)
(D)
B
例题学习
2.2二元一次方程组
例 北京2008年奥运会跳水决赛的门票价格如下表:
小聪购买了B等级和C等级的跳水决赛门票共6张,他发现购买这6张门票所花的钱恰好能购买3张A等级门票,如果设小聪购买B等级和C等级门票分别是x张和y张,请根据问题中的条件列出关于x,y的方程组,并用列表尝试的方法求两种门票的数量。
等级 A B C
票价(元/张) 500 300 150
问1:情境中哪些是已知,哪些是未知的?
问2:情境中哪些语句能帮助你得到数量关系?
解:根据条件可列出关于x,y的方程组
x
y
300x+150y
0
1
2
3
4
5
6
6
5
4
3
2
1
0
900
1050
1200
1350
1500
1650
1800
思考:表格中x的值你会取哪些数?为什么?
可见,只有x=4,y=2 符合这个方程组,所以方程组的解是
x=4
y=2
答:小聪买了B等级跳水决赛门票4张,C等级跳水决赛门票2张.
例题学习
2.2二元一次方程组
课堂小结
二元一次方程组
概念
解
如何求解
注:二元一次方程组并不要求每个方程都是二元的.
列表尝试法
同时满足二元一次方程组中各个方程的解,叫做这个二元一次方程组的解.
课堂小结
一元一次方程的解 二元一次方程的解 二元一次方程组的解
个数
解的形式
1个
无数个
1个
一个未知数的值
一对未知数的值
一对未知数的值
思考:是不是所有二元一次方程组都有唯一解呢?
课后思考
“鸡兔同笼,上有九头,下有二十八足,问鸡兔几何?”
思考:明明用一元一次方程就能又快又简单地解得最终答案,为什么要用二元一次方程组来解决问题呢?
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
