浙教版数学七年级下册 3.4 乘法公式 课件(共18张PPT)
文档属性
| 名称 | 浙教版数学七年级下册 3.4 乘法公式 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-04 22:58:16 | ||
图片预览






文档简介
(共18张PPT)
3.4乘法公式(2)
b
b
a
a
(a+b)
a
b
ab
ab
+
+
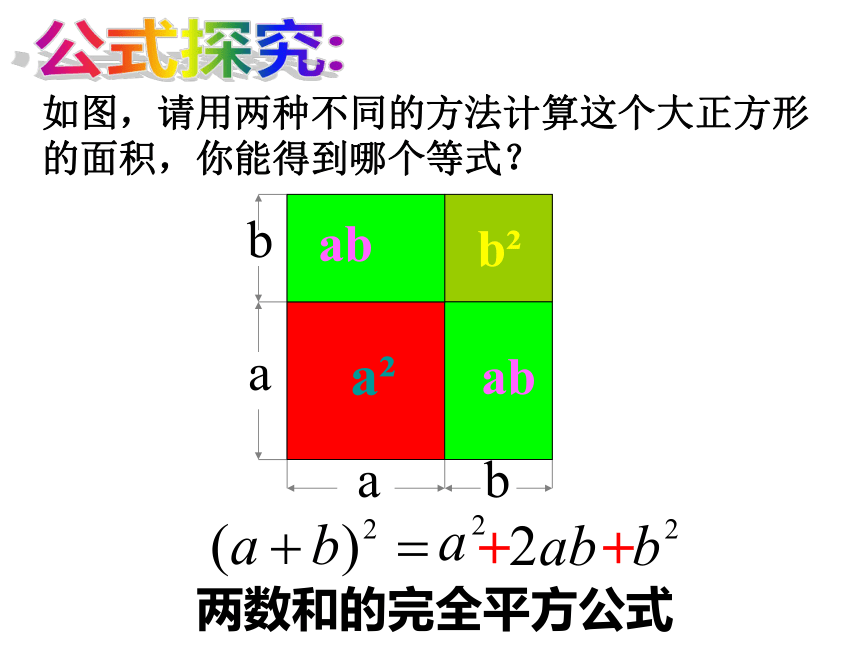
两数和的完全平方公式
如图,请用两种不同的方法计算这个大正方形的面积,你能得到哪个等式?
公式探究:
(a+b)2=
a2
+ b2
两数和的完全平方公式
两数和的平方,等于这两数的平方和,加上这两数积的2倍
+2ab
口诀
首平方,尾平方,两倍首尾中间放
(首+尾)2=首2+2×首×尾+尾2
想一想 若将 中的“+”改为“-”,则
你有几种计算方法?
方法一:
方法二:
方法三:
(a-b)2 = a2-2ab+b2
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
完全平方公式
首平方,尾平方,首尾两倍中间放,符号看前方
以上两个公式统称完全平方公式.
平方差公式和完全平方公式也称乘法公式.
公式当中a,b的可以代表一个数,或一个单项式,多项式
与 相等吗?
与 相等吗?
互为相反数的偶次幂相等
与 相等吗?
比较下列各式之间的关系:
=
≠
(a+b)(-a-b)
= -(a+b)2
=
例1 用完全平方公式计算:
(1)(x+3y)2 (2)(2a-3)2
(3) (-3s+t)2 (4) (-4x-3y)2
方法总结:
确定中间项符号
要点部分:
下列各式的计算错在哪里?应怎样改正?
(1) (x+y)2 = x2 +y2
(2) (a –b)2 = a2 -b2
(4) (a+2b)2 = a2+2ab+2b2
(3) (x– 1)2 = x2 – 2x
(5) (2+x)2 = 2 + 4x+ x2
纠错练习:
活用公式:
1、用简便的方法计算:
(3)1.232+2.46×0.77+0.772
(1) 0.982 (2) 1012
例4:一花农有4块正方形茶花苗圃,边长分别为30.1m,29.5m,30m,27m。现将这4块苗圃的边长都增加1.5m,求各苗圃的面积分别增加了多少m ?
解:设原正方形苗圃边长为am,
∴新正方形的边长为(a+1.5)m,
(a+1.5)2-a2=a2+3a+2.25-a2=3a+2.25
当a=30.1时,
3a+2.25=3×30.1+2.25=92.55
当a=29.5时,
3a+2.25=3×29.5+2.25=90.75
类似地,当a=30, a=27时, 3a+2.25的值分别为92.25,83.25
答:苗圃面积分别增加了92.55m2,90.75m2 92.25m2,83.25m2.
a
a
1.5
1.5
生活在线:
要给一边长为a米的正方形桌子辅上正方形的桌布,桌布的四周均超出桌面0.1米,问需要多大面积的桌布?
解:由题意知,桌布的边长为(a+0.2)米
∴(a+0.2 )2 = a2 +0.4a+0.04(平方米)
答:所需桌布面积为a2+0.4a+0.04(平方米)
提高题
1.填空题:
(1+___ )2= 1+4x+4x2 ;
(2) (3x-___)2= 9x2-12xy+______.
2、计算:
发散思维,勇于创新
1.如果x2-6x+N是一个完全平方式,那么N是( )
(A ) 11 (B) 9 (C) -11 (D) -9
B
2、若 ,则 = 。
巩固提高
1、已知 求 的值。
2.已知(a+b)2=11 , ab=1 , 求(a-b)2的值.
思考 循着 的研究思路,我们还有一些值得研究的问题…
杨辉三角
你能计算 和 吗?
…
六.
计算:
方法一:
方法二:
整体思想
数形结合思想
六.
完全平方公式
多项式相乘
顺用
逆用
数形结合思想
整体思想
转化思想
巧用
3.4乘法公式(2)
b
b
a
a
(a+b)
a
b
ab
ab
+
+
两数和的完全平方公式
如图,请用两种不同的方法计算这个大正方形的面积,你能得到哪个等式?
公式探究:
(a+b)2=
a2
+ b2
两数和的完全平方公式
两数和的平方,等于这两数的平方和,加上这两数积的2倍
+2ab
口诀
首平方,尾平方,两倍首尾中间放
(首+尾)2=首2+2×首×尾+尾2
想一想 若将 中的“+”改为“-”,则
你有几种计算方法?
方法一:
方法二:
方法三:
(a-b)2 = a2-2ab+b2
(a+b)2= a2 +2ab+b2
(a-b)2= a2 - 2ab+b2
完全平方公式
首平方,尾平方,首尾两倍中间放,符号看前方
以上两个公式统称完全平方公式.
平方差公式和完全平方公式也称乘法公式.
公式当中a,b的可以代表一个数,或一个单项式,多项式
与 相等吗?
与 相等吗?
互为相反数的偶次幂相等
与 相等吗?
比较下列各式之间的关系:
=
≠
(a+b)(-a-b)
= -(a+b)2
=
例1 用完全平方公式计算:
(1)(x+3y)2 (2)(2a-3)2
(3) (-3s+t)2 (4) (-4x-3y)2
方法总结:
确定中间项符号
要点部分:
下列各式的计算错在哪里?应怎样改正?
(1) (x+y)2 = x2 +y2
(2) (a –b)2 = a2 -b2
(4) (a+2b)2 = a2+2ab+2b2
(3) (x– 1)2 = x2 – 2x
(5) (2+x)2 = 2 + 4x+ x2
纠错练习:
活用公式:
1、用简便的方法计算:
(3)1.232+2.46×0.77+0.772
(1) 0.982 (2) 1012
例4:一花农有4块正方形茶花苗圃,边长分别为30.1m,29.5m,30m,27m。现将这4块苗圃的边长都增加1.5m,求各苗圃的面积分别增加了多少m ?
解:设原正方形苗圃边长为am,
∴新正方形的边长为(a+1.5)m,
(a+1.5)2-a2=a2+3a+2.25-a2=3a+2.25
当a=30.1时,
3a+2.25=3×30.1+2.25=92.55
当a=29.5时,
3a+2.25=3×29.5+2.25=90.75
类似地,当a=30, a=27时, 3a+2.25的值分别为92.25,83.25
答:苗圃面积分别增加了92.55m2,90.75m2 92.25m2,83.25m2.
a
a
1.5
1.5
生活在线:
要给一边长为a米的正方形桌子辅上正方形的桌布,桌布的四周均超出桌面0.1米,问需要多大面积的桌布?
解:由题意知,桌布的边长为(a+0.2)米
∴(a+0.2 )2 = a2 +0.4a+0.04(平方米)
答:所需桌布面积为a2+0.4a+0.04(平方米)
提高题
1.填空题:
(1+___ )2= 1+4x+4x2 ;
(2) (3x-___)2= 9x2-12xy+______.
2、计算:
发散思维,勇于创新
1.如果x2-6x+N是一个完全平方式,那么N是( )
(A ) 11 (B) 9 (C) -11 (D) -9
B
2、若 ,则 = 。
巩固提高
1、已知 求 的值。
2.已知(a+b)2=11 , ab=1 , 求(a-b)2的值.
思考 循着 的研究思路,我们还有一些值得研究的问题…
杨辉三角
你能计算 和 吗?
…
六.
计算:
方法一:
方法二:
整体思想
数形结合思想
六.
完全平方公式
多项式相乘
顺用
逆用
数形结合思想
整体思想
转化思想
巧用
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
