浙教版七年级下册 5.2.1 分式的基本性质 课件(共17张PPT)
文档属性
| 名称 | 浙教版七年级下册 5.2.1 分式的基本性质 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 401.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-05 20:32:59 | ||
图片预览






文档简介
(共17张PPT)
5.2.1 分式的基本性质
温故知新
分数的基本性质
上列各数中,哪些数相等?请说明理由.
分数的分子与分母都乘(或除以)同一个不等于零的数,分数的值不变.
性质猜想
分数的基本性质
分数的分子与分母都乘(或除以)同一个不等于零的数 ,分数的值不变.
分式的基本性质
分式
整式
分式
( 其中 是不等于零的数 )
整式
性质推导
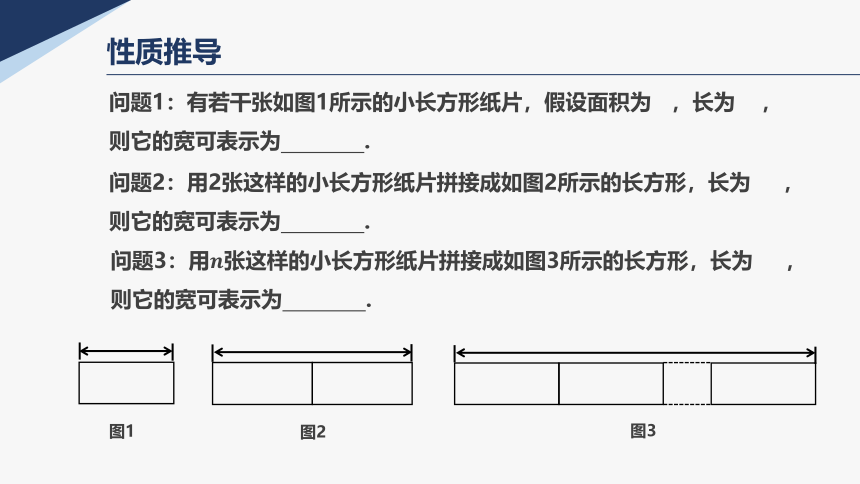
问题1:有若干张如图1所示的小长方形纸片,假设面积为 ,长为 ,
则它的宽可表示为 .
问题2:用2张这样的小长方形纸片拼接成如图2所示的长方形,长为 ,则它的宽可表示为 .
图1
图3
问题3:用张这样的小长方形纸片拼接成如图3所示的长方形,长为 ,则它的宽可表示为 .
图2
性质归纳
分式的分子与分母都乘(或除以)同一个不等于零的整式,分式的值不变.
分式的基本性质
(其中 是不等于零的整式)
性质辨析
√
√
×
×
×
×
判一判:下列各式从左到右的变形是否正确?说明理由.
(1)
(2)
性质应用
填一填:
化整
做一做:不改变分式的值,把下列分式的分子与分母中各项的系数都化为整数.
(1) (2)
系数为分数时:
同乘以系数的分母的最小公倍数.
系数为小数时:
一般情况下,同乘以10的倍数.
(1) (2) (3)
做一做:不改变分式的值,把下列分式的分子与分母的最高次项的系数都化为正数.
法则探索
上列分式中,哪些分式相等?
分式的符号法则
分子、分母及分式的符号,改变其中任何 个,分式的值不变.
两
法则探索
试一试:不改变分式的值,使下列分式的分子与分母都不含“”号.
(1) (2) (3)
化正
做一做:不改变分式的值,把下列分式的分子与分母的最高次项的系数都化为正数.
(1) (2) (3)
(1)分子、分母降幂排列;
(2)若首项为负,则添上带“”的括号;
(3)化去分子分母中的“” .
约分
例1. 化简下列分式:
(1) (2)
分子、分母都是单项式时:
直接约去最大公因式.
分子、分母中含有多项式:
先因式分解;再约去最大公因式.
分式的约分:约去一个分式的分子和分母的公因式.
最简分式:分子、分母不含公因式.
(1) (2)
练习巩固
练1-1化简下列分式:
(3) (4)
练1-2用分式表示下列各式的商,并约分:
课堂小结
分式的分子与分母都乘(或除以)同一个不等于零的整式,分式的值不变.
分式的基本性质
(其中 是不等于零的整式)
符号法则
化整
化正
约分
最简
分式
1.先因式分解
2.再约去最大公因式
1.所有系数都为整数;
2.首项系数为正.
知识
应用
方法
特殊
一般
类比
稳步提升
练2. 化简下列各式:
(1) (2)
拓展提升
拓1:如图,为了制作贺卡,需在边长为 的正方形纸片上剪下边长为的正方形。若合理剪裁可将剩下的纸片恰好拼成一长为 的长方形,拼成的长方形的宽是多少
2
+
5.2.1 分式的基本性质
温故知新
分数的基本性质
上列各数中,哪些数相等?请说明理由.
分数的分子与分母都乘(或除以)同一个不等于零的数,分数的值不变.
性质猜想
分数的基本性质
分数的分子与分母都乘(或除以)同一个不等于零的数 ,分数的值不变.
分式的基本性质
分式
整式
分式
( 其中 是不等于零的数 )
整式
性质推导
问题1:有若干张如图1所示的小长方形纸片,假设面积为 ,长为 ,
则它的宽可表示为 .
问题2:用2张这样的小长方形纸片拼接成如图2所示的长方形,长为 ,则它的宽可表示为 .
图1
图3
问题3:用张这样的小长方形纸片拼接成如图3所示的长方形,长为 ,则它的宽可表示为 .
图2
性质归纳
分式的分子与分母都乘(或除以)同一个不等于零的整式,分式的值不变.
分式的基本性质
(其中 是不等于零的整式)
性质辨析
√
√
×
×
×
×
判一判:下列各式从左到右的变形是否正确?说明理由.
(1)
(2)
性质应用
填一填:
化整
做一做:不改变分式的值,把下列分式的分子与分母中各项的系数都化为整数.
(1) (2)
系数为分数时:
同乘以系数的分母的最小公倍数.
系数为小数时:
一般情况下,同乘以10的倍数.
(1) (2) (3)
做一做:不改变分式的值,把下列分式的分子与分母的最高次项的系数都化为正数.
法则探索
上列分式中,哪些分式相等?
分式的符号法则
分子、分母及分式的符号,改变其中任何 个,分式的值不变.
两
法则探索
试一试:不改变分式的值,使下列分式的分子与分母都不含“”号.
(1) (2) (3)
化正
做一做:不改变分式的值,把下列分式的分子与分母的最高次项的系数都化为正数.
(1) (2) (3)
(1)分子、分母降幂排列;
(2)若首项为负,则添上带“”的括号;
(3)化去分子分母中的“” .
约分
例1. 化简下列分式:
(1) (2)
分子、分母都是单项式时:
直接约去最大公因式.
分子、分母中含有多项式:
先因式分解;再约去最大公因式.
分式的约分:约去一个分式的分子和分母的公因式.
最简分式:分子、分母不含公因式.
(1) (2)
练习巩固
练1-1化简下列分式:
(3) (4)
练1-2用分式表示下列各式的商,并约分:
课堂小结
分式的分子与分母都乘(或除以)同一个不等于零的整式,分式的值不变.
分式的基本性质
(其中 是不等于零的整式)
符号法则
化整
化正
约分
最简
分式
1.先因式分解
2.再约去最大公因式
1.所有系数都为整数;
2.首项系数为正.
知识
应用
方法
特殊
一般
类比
稳步提升
练2. 化简下列各式:
(1) (2)
拓展提升
拓1:如图,为了制作贺卡,需在边长为 的正方形纸片上剪下边长为的正方形。若合理剪裁可将剩下的纸片恰好拼成一长为 的长方形,拼成的长方形的宽是多少
2
+
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
