浙教版数学七年级下册 5.5.1 分式方程 课件(共15张PPT)
文档属性
| 名称 | 浙教版数学七年级下册 5.5.1 分式方程 课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 633.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-06 10:59:51 | ||
图片预览




文档简介
(共15张PPT)
《数学》(浙江版 七年级 下册)
5.5 分式方程(1)
分式方程的概念及解法
某地电话公司调低了长途电话的话费标准,每分费用降低了25%,因此按原收费标准6元话费的通话时间,在新收费标准下可多通话5分时间,问前后两种收费标准每分收费各是多少
合作学习
在上面的问题中,主要等量关系是什么
6元话费 按原收费标准的通话时间+5
= 按新收费标准的通话时间
=
+5
如果设原来的收费标准是 元/分,可列怎样的方程
下列各方程有什么共同的特点?
以上这些方程有什么共同的特点吗?
像这样只含分式,或分式和整式,并且分母里含有未知数的方程叫做分式方程.
下列方程中,哪些是分式方程?哪些不是分式方程?为什么?
不是
不是
是
是
不是
辨一辨
不是
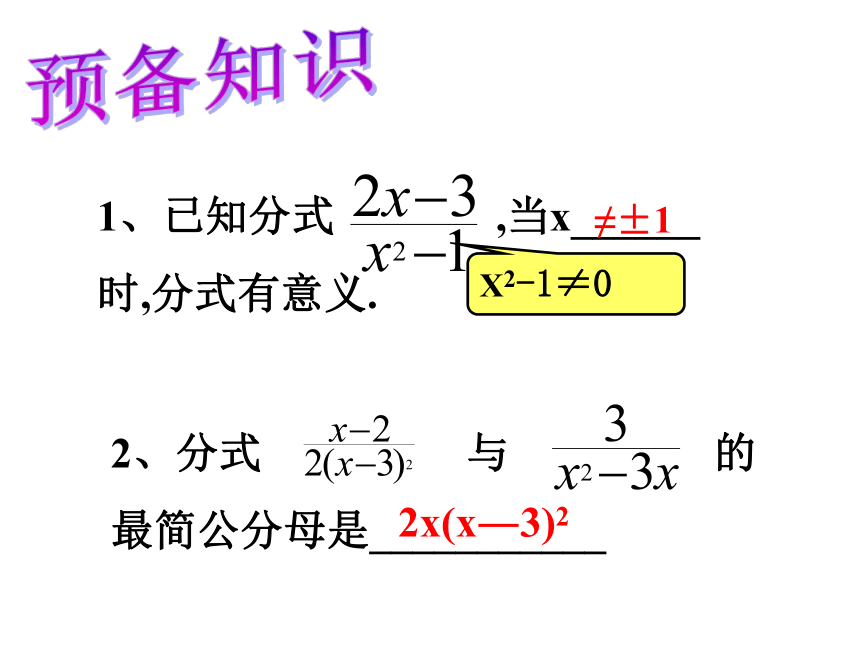
1、已知分式 ,当x______
时,分式有意义.
2、分式 与 的
最简公分母是___________
X2-1≠0
≠±1
2x(x―3)2
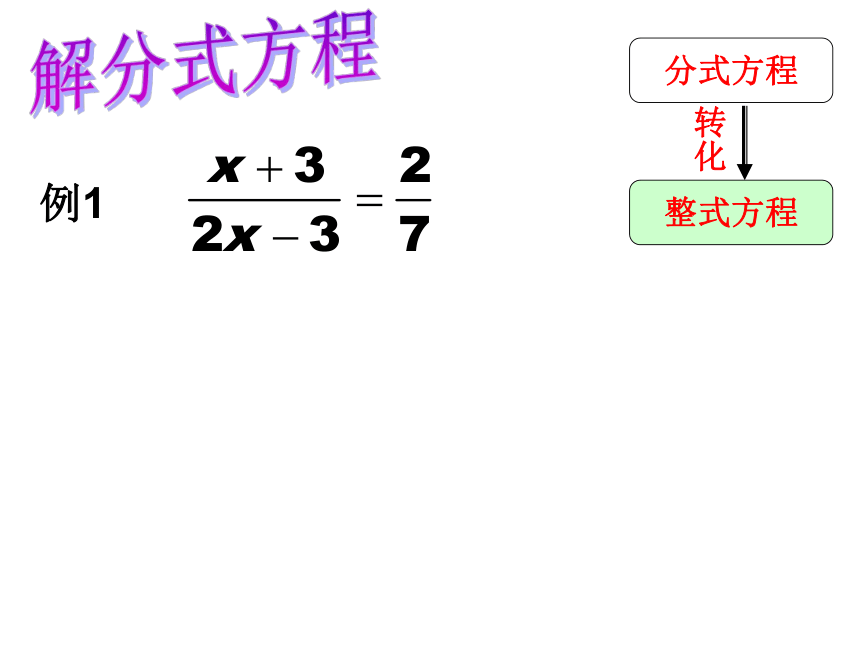
分式方程
整式方程
转化
例1
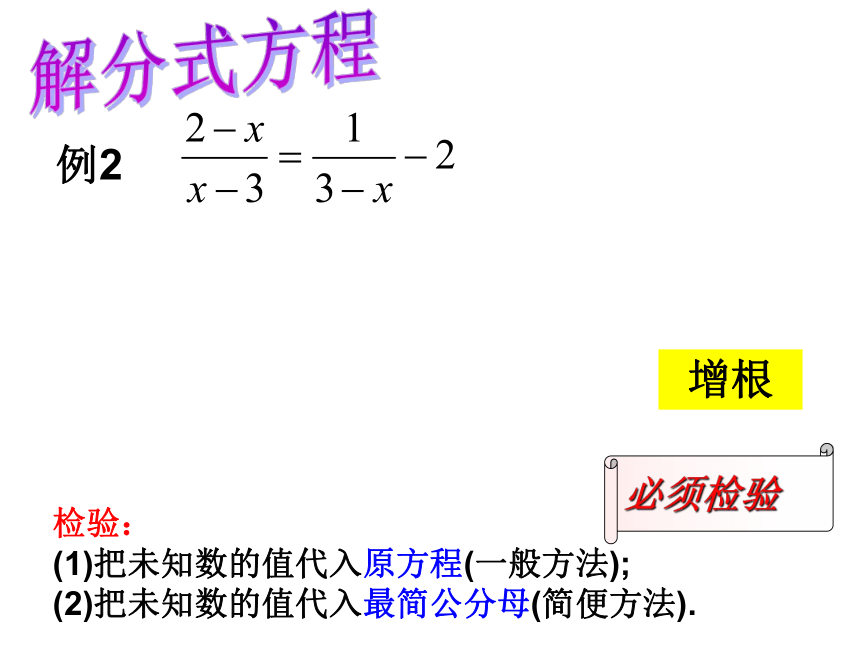
例2
增根
必须检验
检验:
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
解分式方程的一般步骤:
1.去分母(方程两边同乘以最简公分母),把分式方程转化为整式方程;
2.解这个整式方程;
3. 验根,写出方程的解(把方程的解代入最简公分母,使最简公分母为零的根是增根,应舍去).
转化
验根
纠错:下列运算对吗?如果不对,请改正
两边去分母 得 x -2= - 3 ∴x= -1
(1)
(2)
两边去分母 得
∴x= 4
(3)
两边去分母 得
∴x= -2
解方程:
拓展提高
(2)方程会产生增根
(3)方程无解
解分式方程一般需要哪几个步骤
去分母,化为整式方程:
⑴把各分母分解因式;
⑵找出各分母的最简公分母;
⑶方程两边各项乘以最简公分母;
解整式方程.
检验.
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
结论 :确定分式方程的解.
解题小结
这里的检验要以计算正确为前提
解分式方程容易犯的错误主要有:
(1)去分母时,原方程整式部分漏乘即每一项都需乘以最简公分母。
(2)约去分母后,分子是多项式时, 要注意添括号.
(3)增根不舍掉.
(4)……
想一想
(填空)1、解方程:
解:方程两边同乘以 ,
化简,得 .
解得 x1= , x2= .
检验:把x1= ,代入最简公分母,
x(x-2)= = ≠0;
把x2= ,代入最简公分母,
x(x-2)= =0
∴x= 是增根,舍去. ∴原方程的根是x= .
x(x-2)
x 2+ x -6=0 或x(x+1)-6=0
-3 2
-3
-3(-3-2) 15
2
2(2-2)
2
-3
············
·· ·······
① ② ③
课堂检测
2、分式方程 的最简公分母是 .
3、如果 有增根,那么增根为 .
5、若分式方程 有增根x=2,则
a= .
X=2
X-1
分析:
原分式方程去分母,两边同乘以(x2 -4),得 a(x+2)+4=0 ①
把x=2代入整式方程①,得 4a+4=0, a=-1
∴ a=-1时,x=2是原方程的增根.
-1
4、关于x的方程 =4 的解是x= ,则a= .
2
《数学》(浙江版 七年级 下册)
5.5 分式方程(1)
分式方程的概念及解法
某地电话公司调低了长途电话的话费标准,每分费用降低了25%,因此按原收费标准6元话费的通话时间,在新收费标准下可多通话5分时间,问前后两种收费标准每分收费各是多少
合作学习
在上面的问题中,主要等量关系是什么
6元话费 按原收费标准的通话时间+5
= 按新收费标准的通话时间
=
+5
如果设原来的收费标准是 元/分,可列怎样的方程
下列各方程有什么共同的特点?
以上这些方程有什么共同的特点吗?
像这样只含分式,或分式和整式,并且分母里含有未知数的方程叫做分式方程.
下列方程中,哪些是分式方程?哪些不是分式方程?为什么?
不是
不是
是
是
不是
辨一辨
不是
1、已知分式 ,当x______
时,分式有意义.
2、分式 与 的
最简公分母是___________
X2-1≠0
≠±1
2x(x―3)2
分式方程
整式方程
转化
例1
例2
增根
必须检验
检验:
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
解分式方程的一般步骤:
1.去分母(方程两边同乘以最简公分母),把分式方程转化为整式方程;
2.解这个整式方程;
3. 验根,写出方程的解(把方程的解代入最简公分母,使最简公分母为零的根是增根,应舍去).
转化
验根
纠错:下列运算对吗?如果不对,请改正
两边去分母 得 x -2= - 3 ∴x= -1
(1)
(2)
两边去分母 得
∴x= 4
(3)
两边去分母 得
∴x= -2
解方程:
拓展提高
(2)方程会产生增根
(3)方程无解
解分式方程一般需要哪几个步骤
去分母,化为整式方程:
⑴把各分母分解因式;
⑵找出各分母的最简公分母;
⑶方程两边各项乘以最简公分母;
解整式方程.
检验.
(1)把未知数的值代入原方程(一般方法);
(2)把未知数的值代入最简公分母(简便方法).
结论 :确定分式方程的解.
解题小结
这里的检验要以计算正确为前提
解分式方程容易犯的错误主要有:
(1)去分母时,原方程整式部分漏乘即每一项都需乘以最简公分母。
(2)约去分母后,分子是多项式时, 要注意添括号.
(3)增根不舍掉.
(4)……
想一想
(填空)1、解方程:
解:方程两边同乘以 ,
化简,得 .
解得 x1= , x2= .
检验:把x1= ,代入最简公分母,
x(x-2)= = ≠0;
把x2= ,代入最简公分母,
x(x-2)= =0
∴x= 是增根,舍去. ∴原方程的根是x= .
x(x-2)
x 2+ x -6=0 或x(x+1)-6=0
-3 2
-3
-3(-3-2) 15
2
2(2-2)
2
-3
············
·· ·······
① ② ③
课堂检测
2、分式方程 的最简公分母是 .
3、如果 有增根,那么增根为 .
5、若分式方程 有增根x=2,则
a= .
X=2
X-1
分析:
原分式方程去分母,两边同乘以(x2 -4),得 a(x+2)+4=0 ①
把x=2代入整式方程①,得 4a+4=0, a=-1
∴ a=-1时,x=2是原方程的增根.
-1
4、关于x的方程 =4 的解是x= ,则a= .
2
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
