浙教版七年级下册 第二章 二元一次方程组 复习学案(无答案)
文档属性
| 名称 | 浙教版七年级下册 第二章 二元一次方程组 复习学案(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 156.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-09 00:00:00 | ||
图片预览

文档简介
七下第二章 二元一次方程组复习学案
班级: 姓名:
复习目标: 1.了解二元一次方程和二元一次方程组的概念;
2.掌握代入消元法和加减消元法;
3.用方程组解决实际问题。
例题讲解:
例1:关于x、y方程(k2-1)x2+(k+1)x+2ky=k+3,当k= ______ 时,它为一元一次方程,
当k= ______ 时,它为二元一次方程.
例2:已知m为正整数,且关于x,y的二元一次方程组有整数解,则m2的值为( )A.4: B.1,4 C.1,4,49 D.无法确定
例3:已知关于,的方程组,给出下列结论:①是方程组的一个解; ②当时,,的值互为相反数; ③当时,方程组的解也是方程的解;④,间的数量关系是.其中正确的是( )
A.②③ B.①②③ C.②③④ D.①②③④
例4:(2018·湖北武汉中考)将正整数1至2 018按一定规律排列如下表:
平移表中带阴影的方框,方框中三个数的和可能是( )
A.2 019 B.2 018 C.2 016 D.2 013
例5:.已知关于x,y的方程组的解为正数,则|k-6|+|k+1|= .
例6:关于x,y的二元一次方程(a-1)x+(a+2)y+5-2a=0,当a取一个确定的值时就得到一个方程,所有这些方程有一个公共解,则这个公共解是( ).
例7:已知t满足方程组 则x和y之间满足的关系是x= .
例8:若方程的解为,则方程组
的解为___ __________
例9:甲、乙两人同解方程组 时,甲看错了方程①中的a,解得,乙看错了②中的b,解得 HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4 的值.2
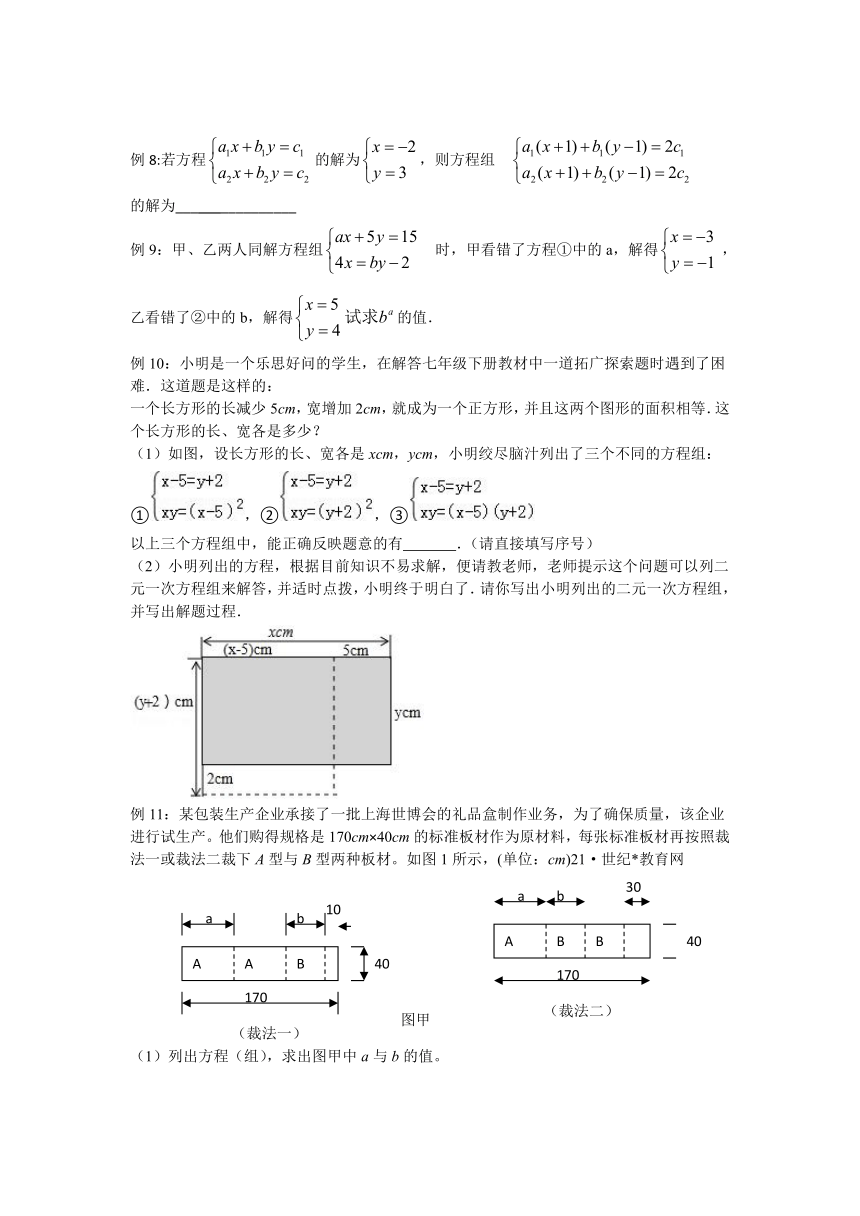
例10:小明是一个乐思好问的学生,在解答七年级下册教材中一道拓广探索题时遇到了困难.这道题是这样的:
一个长方形的长减少5cm,宽增加2cm,就成为一个正方形,并且这两个图形的面积相等.这个长方形的长、宽各是多少?
(1)如图,设长方形的长、宽各是xcm,ycm,小明绞尽脑汁列出了三个不同的方程组:
①,②,③
以上三个方程组中,能正确反映题意的有 .(请直接填写序号)
(2)小明列出的方程,根据目前知识不易求解,便请教老师,老师提示这个问题可以列二元一次方程组来解答,并适时点拨,小明终于明白了.请你写出小明列出的二元一次方程组,并写出解题过程.
例11:某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产。他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材。如图1所示,(单位:cm)21·世纪*教育网
(1)列出方程(组),求出图甲中a与b的值。
(2)在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙的竖式与横式两种无盖礼品盒。
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:
竖式无盖(个) 横式无盖(个)
x y
A型(张) 4x 3y
B型(张) x
③做成的竖式和横式两种无盖礼品盒总数最多是 个;
此时,横式无盖礼品盒可以做 个。
例12:在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建一条210米长的公路,甲队每天修建15米,乙队每天修建25米,一共用10天完成.
根据题意,小红和小芳同学分别列出了下面尚不完整的方程组:
小红:小芳:
(1)请你分别写出小红和小芳所列方程组中未知数x,y表示的意义:
小红:x表示 ,y表示 ;
小芳:x表示 ,y表示 ;
(2)在题中“( )”内把小红和小芳所列方程组补充完整;
(3)甲工程队一共修建了 天,乙工程队一共修建了 米.
例13:我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[﹣2.5]=﹣3,用<a>表示大于a的最小整数.例如:<2.5>=3,<4>=5,<﹣1.5>=﹣1.解决下列问题:
(1)[﹣2.6]= ,<6.2>= .
(2)已知x,y满足方程组,则[x]= ,<y>= ,x的取值范围是 ,y的取值范围是 .
例14:某校举办“迎亚运“学生书画展览,现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品.
(1)如图1,若大长方形的长和宽分别为45米和30米,求小长方形的长和宽.
(2)如图2,若大长方形的长和宽分别为a和b
①直接写出1个小长方形周长与大长方形周长之比;
②若作品展览区域(阴影部分)面积占展厅面积的,试求的值.
例15:.[阅读 领会]
怎样判断两条直线是否平行?
如图①,很难看出直线a、b是否平行,可添加“第三条线”(截线c),把判断两条直线的位置关系转化为判断两个角的数量关系.我们称直线c为“辅助线”.
在部分代数问题中,很难用算术直接计算出结果,于是,引入字母解决复杂问题,我们称引入的字母为“辅助元素”
事实上,使用“辅助线”、“辅助元”等“辅助元素”可以更容易地解决问题
【实践 体悟】
(1)计算(2+++)(+++)—(++)(2++++),这个算式直接计算很麻烦,请你引入合适的“辅助元”完成计算
(2)如图②,已知∠C+∠E=∠EAB,求证AB∥CD,请你添加适当的“辅助线”,并完成证明
【创造 突破】
(3)若关于xy的方程组的解是的解是 则关于x、y的方程组的解为
(4)如图③∠A1=∠A5=120°,∠A2=∠A4=70°,∠A6=∠A8=90°,我们把大于平角的角称为“优角”,若优角∠A3=270°,则优角∠A7=
例16:小明和小红同解同一个方程组时,小红不慎将一滴墨水滴在了题目上使得方程组的系数看不清了,显示如下,同桌的小明说:“我正确的求出这个方程组的解为”,而小红说:“我求出的解是,于是小红检查后发现,这是她看错了方程组中第二个方程中x的系数所致”,请你根据他们的对话,把原方程组还原出来.
A
B
B
170
40
a
b
30
(裁法二)
图甲
b
170
a
40
A
A
B
10
(裁法一)
图乙
礼品盒
板 材
班级: 姓名:
复习目标: 1.了解二元一次方程和二元一次方程组的概念;
2.掌握代入消元法和加减消元法;
3.用方程组解决实际问题。
例题讲解:
例1:关于x、y方程(k2-1)x2+(k+1)x+2ky=k+3,当k= ______ 时,它为一元一次方程,
当k= ______ 时,它为二元一次方程.
例2:已知m为正整数,且关于x,y的二元一次方程组有整数解,则m2的值为( )A.4: B.1,4 C.1,4,49 D.无法确定
例3:已知关于,的方程组,给出下列结论:①是方程组的一个解; ②当时,,的值互为相反数; ③当时,方程组的解也是方程的解;④,间的数量关系是.其中正确的是( )
A.②③ B.①②③ C.②③④ D.①②③④
例4:(2018·湖北武汉中考)将正整数1至2 018按一定规律排列如下表:
平移表中带阴影的方框,方框中三个数的和可能是( )
A.2 019 B.2 018 C.2 016 D.2 013
例5:.已知关于x,y的方程组的解为正数,则|k-6|+|k+1|= .
例6:关于x,y的二元一次方程(a-1)x+(a+2)y+5-2a=0,当a取一个确定的值时就得到一个方程,所有这些方程有一个公共解,则这个公共解是( ).
例7:已知t满足方程组 则x和y之间满足的关系是x= .
例8:若方程的解为,则方程组
的解为___ __________
例9:甲、乙两人同解方程组 时,甲看错了方程①中的a,解得,乙看错了②中的b,解得 HYPERLINK "http://www.21cnjy.com/" EMBED Equation.DSMT4 的值.2
例10:小明是一个乐思好问的学生,在解答七年级下册教材中一道拓广探索题时遇到了困难.这道题是这样的:
一个长方形的长减少5cm,宽增加2cm,就成为一个正方形,并且这两个图形的面积相等.这个长方形的长、宽各是多少?
(1)如图,设长方形的长、宽各是xcm,ycm,小明绞尽脑汁列出了三个不同的方程组:
①,②,③
以上三个方程组中,能正确反映题意的有 .(请直接填写序号)
(2)小明列出的方程,根据目前知识不易求解,便请教老师,老师提示这个问题可以列二元一次方程组来解答,并适时点拨,小明终于明白了.请你写出小明列出的二元一次方程组,并写出解题过程.
例11:某包装生产企业承接了一批上海世博会的礼品盒制作业务,为了确保质量,该企业进行试生产。他们购得规格是170cm×40cm的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下A型与B型两种板材。如图1所示,(单位:cm)21·世纪*教育网
(1)列出方程(组),求出图甲中a与b的值。
(2)在试生产阶段,若将30张标准板材用裁法一裁剪,4张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成图乙的竖式与横式两种无盖礼品盒。
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒x个,横式无盖礼品盒的y个,根据题意完成表格:
竖式无盖(个) 横式无盖(个)
x y
A型(张) 4x 3y
B型(张) x
③做成的竖式和横式两种无盖礼品盒总数最多是 个;
此时,横式无盖礼品盒可以做 个。
例12:在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建一条210米长的公路,甲队每天修建15米,乙队每天修建25米,一共用10天完成.
根据题意,小红和小芳同学分别列出了下面尚不完整的方程组:
小红:小芳:
(1)请你分别写出小红和小芳所列方程组中未知数x,y表示的意义:
小红:x表示 ,y表示 ;
小芳:x表示 ,y表示 ;
(2)在题中“( )”内把小红和小芳所列方程组补充完整;
(3)甲工程队一共修建了 天,乙工程队一共修建了 米.
例13:我们用[a]表示不大于a的最大整数,例如:[2.5]=2,[3]=3,[﹣2.5]=﹣3,用<a>表示大于a的最小整数.例如:<2.5>=3,<4>=5,<﹣1.5>=﹣1.解决下列问题:
(1)[﹣2.6]= ,<6.2>= .
(2)已知x,y满足方程组,则[x]= ,<y>= ,x的取值范围是 ,y的取值范围是 .
例14:某校举办“迎亚运“学生书画展览,现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品.
(1)如图1,若大长方形的长和宽分别为45米和30米,求小长方形的长和宽.
(2)如图2,若大长方形的长和宽分别为a和b
①直接写出1个小长方形周长与大长方形周长之比;
②若作品展览区域(阴影部分)面积占展厅面积的,试求的值.
例15:.[阅读 领会]
怎样判断两条直线是否平行?
如图①,很难看出直线a、b是否平行,可添加“第三条线”(截线c),把判断两条直线的位置关系转化为判断两个角的数量关系.我们称直线c为“辅助线”.
在部分代数问题中,很难用算术直接计算出结果,于是,引入字母解决复杂问题,我们称引入的字母为“辅助元素”
事实上,使用“辅助线”、“辅助元”等“辅助元素”可以更容易地解决问题
【实践 体悟】
(1)计算(2+++)(+++)—(++)(2++++),这个算式直接计算很麻烦,请你引入合适的“辅助元”完成计算
(2)如图②,已知∠C+∠E=∠EAB,求证AB∥CD,请你添加适当的“辅助线”,并完成证明
【创造 突破】
(3)若关于xy的方程组的解是的解是 则关于x、y的方程组的解为
(4)如图③∠A1=∠A5=120°,∠A2=∠A4=70°,∠A6=∠A8=90°,我们把大于平角的角称为“优角”,若优角∠A3=270°,则优角∠A7=
例16:小明和小红同解同一个方程组时,小红不慎将一滴墨水滴在了题目上使得方程组的系数看不清了,显示如下,同桌的小明说:“我正确的求出这个方程组的解为”,而小红说:“我求出的解是,于是小红检查后发现,这是她看错了方程组中第二个方程中x的系数所致”,请你根据他们的对话,把原方程组还原出来.
A
B
B
170
40
a
b
30
(裁法二)
图甲
b
170
a
40
A
A
B
10
(裁法一)
图乙
礼品盒
板 材
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
