浙教版七年级下册 1.3 平行线的判定 课件(共17张PPT)
文档属性
| 名称 | 浙教版七年级下册 1.3 平行线的判定 课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-10 19:10:59 | ||
图片预览




文档简介
(共17张PPT)
1.3 平行线的判定(1)
P
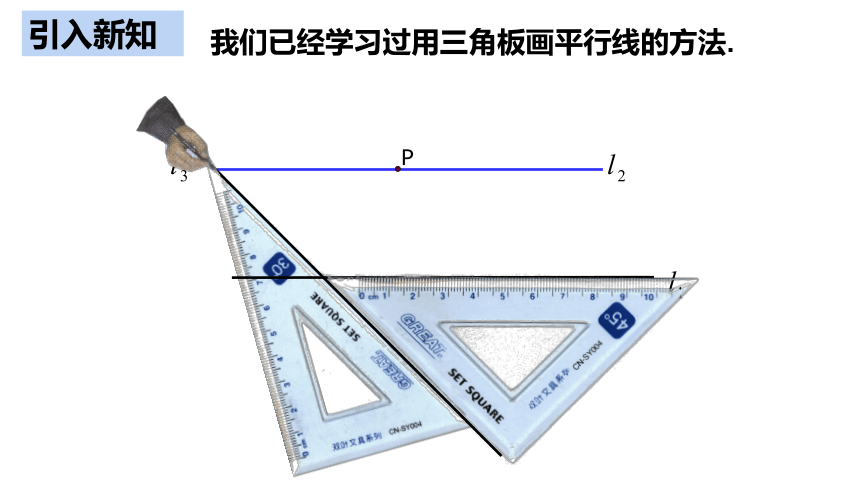
引入新知
我们已经学习过用三角板画平行线的方法.
2
P
1
探索新知
探索新知
平行线的判定方法:
两条直线被第三条直线所截,
如果同位角相等,
那么这两条直线平行.
即同位角相等,两直线平行.
几何语言:
∵∠1=∠2
∴a∥b
(同位角相等,两直线平行)
3
4
6
5
8
7
辨析判定
如图,三根木条相交成∠1,∠2,固定木条b、c,
转动木条a,请问:∠1,∠2满足什么条件时,直线a与
b平行.
当∠1=∠2时,
a∥b
(同位角相等,两直线平行)
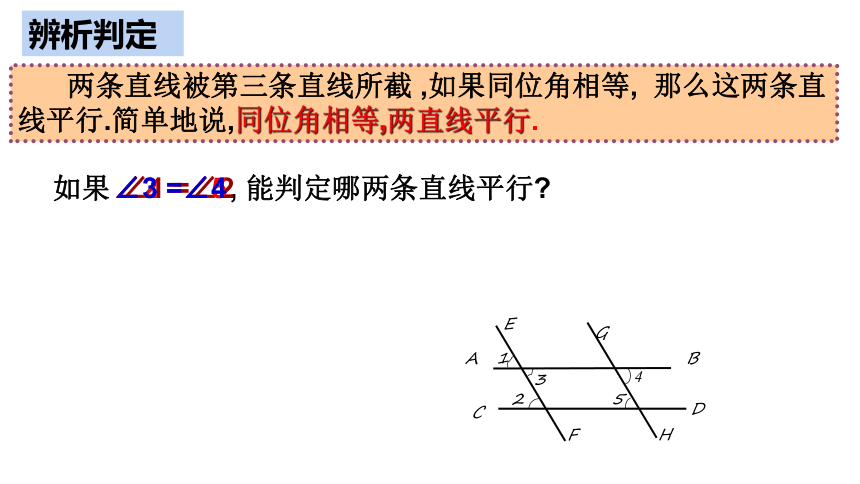
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.简单地说,同位角相等,两直线平行.
4
1
2
3
A
B
C
E
F
D
5
H
G
如果 , 能判定哪两条直线平行
∠1 =∠2
∠2 =∠5
∠3 =∠4
辨析判定
∥
×
√
50°
×
A
B
C
D
E
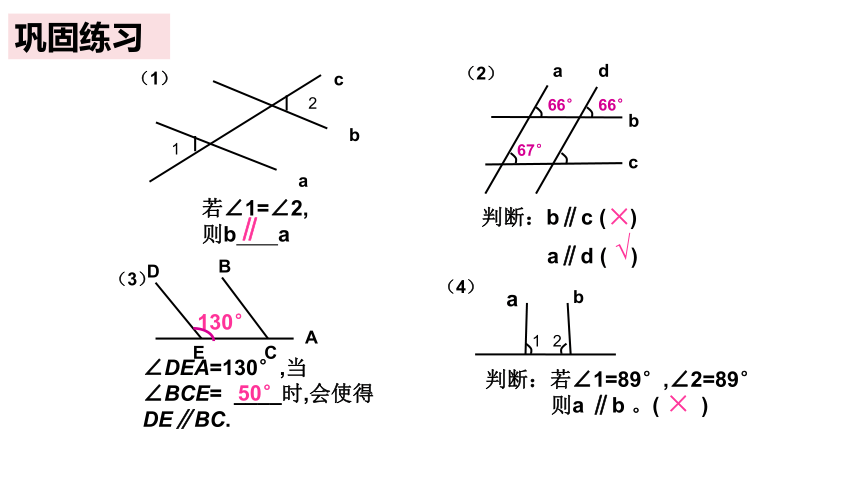
∠DEA=130°,当∠BCE= ____时,会使得DE∥BC.
130°
(1)
(2)
(4)
(3)
a
b
c
1
2
若∠1=∠2,
则b a
判断:b∥c ( )
a∥d ( )
b
c
a
d
66°
66°
67°
1
2
a
b
判断:若∠1=89°,∠2=89°
则a ∥b 。( )
巩固练习
火眼金睛,找出图中的平行线
C
A
D
B
E
F
如果∠ADE=∠ABC,则__∥ __
如果∠ACD=∠F, 则__∥ __
如果∠DEC=∠BCF,则__∥ __
巩固练习
DE
BC
CD
BF
DE
BC
解:∵∠2+∠3=180°且∠2=∠135°
∴∠3=180°- 135°=45°
∵∠1=45°
∴∠1=∠3
∴l1//l2(同位角相等,两直线平行)
例 已知直线 被 所截,如图,
试判断 与 是否平行.并说明理由.
1
2
3
变1:条件弱化为∠1+∠2=180°,结论是否仍然成立?
4
变2:条件变为∠1=∠4,结论是否仍然成立?请说明理由.
变式2:
解:∵∠3=∠4(对顶角相等)
∵∠1=∠4
∴∠1=∠3
∴l1//l2(同位角相等,两直线平行)
变式1:
解:∵∠2+∠3=180°
∵∠1+∠2=180°
∴∠1=∠3
∴l1//l2(同位角相等,两直线平行)
若∠1=45°
,∠2=135
例题讲解
如图,已知∠ABD=∠ACE,BF、CG分别是∠ABD、∠ACE的平分线,请判断BF与CG是否平行,并说明理由。
A
B
C
D
E
F
G
解:
BF∥CG
1
2
∵BF、CG分别是∠ABD、∠ACE的平分线
∴ ∠1= ∠ABD,∠2= ∠ACE
∵
∠ABD=∠ACE
∴ ∠1=∠2
∴
BF∥CG( )
同位角相等,两直线平行
变式练习
如图,木工师傅用角尺画出工件边缘的两条垂线, 则这两条垂线就平行了.为什么呢
解
1
2
(同位角相等,两直线平行)
.
探究与发现——木工师傅为什么可以这样画?
推论:在同一平面内,垂直于同一条直线的两条直线互相平行.
几何语言:
∵a⊥c,b⊥c
∴a∥b
通过观察,我们知道图中一排旗杆都平行。 那么,任意找两根旗杆,请说说明一下它们为什么平行 你是如何作判断的 。
因为旗杆同垂直于经过旗杆与地面交点的直线,所以它们互相平行。
依据:在同一平面内,垂直于同一直线的两直线平行。
探究与发现——旗杆为什么平行
小明骑自行车从A地出发,沿正东方向前进至B处后,右转15°,沿直线向前行驶到C处(如图) .这时他想仍按正东方向行驶,那么他应怎样调整行驶方向?请画出他应继续行驶的路线,并说明理由.
活动—怎样调整行驶方向?
东
15°
1.调整后的路线和原路线所在的直线是什么位置关系?
2.如何理解“怎样调整行驶方向” ?
解: 向左拐 15°.如图
(同位角相等,两直线平行).
∵∠1=∠2=15°
∴AB//CD
画一画:已知直线AB和直线外一点C(如图).你能用一把三角尺过点C画AB的平行线吗?如果能,说明方法,并画出图形.
A
B
C
E
如图,直线CE就是所求的平行线.
D
想一想 如图,AB⊥CD于点B,AE与BF相交于点G,且FGE=60°,∠ABG=30°.判段AE与CD是否平行?
(1)平行线的判定方法。
(2)判定两直线平行的关键步骤:一找到截线与同位角,二说明同位角相等。
(3)注意说理过程的严密性。
(4)体会数学来源于生活,又应用于生活的用数学的思想。
A
B
C
D
E
F
若 AB⊥EF,CD⊥EF
则 AB∥ CD
∵
∴
E
1
2
A
B
C
D
F
∵ ∠.1=∠2
∴ AB∥CD
1.3 平行线的判定(1)
P
引入新知
我们已经学习过用三角板画平行线的方法.
2
P
1
探索新知
探索新知
平行线的判定方法:
两条直线被第三条直线所截,
如果同位角相等,
那么这两条直线平行.
即同位角相等,两直线平行.
几何语言:
∵∠1=∠2
∴a∥b
(同位角相等,两直线平行)
3
4
6
5
8
7
辨析判定
如图,三根木条相交成∠1,∠2,固定木条b、c,
转动木条a,请问:∠1,∠2满足什么条件时,直线a与
b平行.
当∠1=∠2时,
a∥b
(同位角相等,两直线平行)
两条直线被第三条直线所截 ,如果同位角相等, 那么这两条直线平行.简单地说,同位角相等,两直线平行.
4
1
2
3
A
B
C
E
F
D
5
H
G
如果 , 能判定哪两条直线平行
∠1 =∠2
∠2 =∠5
∠3 =∠4
辨析判定
∥
×
√
50°
×
A
B
C
D
E
∠DEA=130°,当∠BCE= ____时,会使得DE∥BC.
130°
(1)
(2)
(4)
(3)
a
b
c
1
2
若∠1=∠2,
则b a
判断:b∥c ( )
a∥d ( )
b
c
a
d
66°
66°
67°
1
2
a
b
判断:若∠1=89°,∠2=89°
则a ∥b 。( )
巩固练习
火眼金睛,找出图中的平行线
C
A
D
B
E
F
如果∠ADE=∠ABC,则__∥ __
如果∠ACD=∠F, 则__∥ __
如果∠DEC=∠BCF,则__∥ __
巩固练习
DE
BC
CD
BF
DE
BC
解:∵∠2+∠3=180°且∠2=∠135°
∴∠3=180°- 135°=45°
∵∠1=45°
∴∠1=∠3
∴l1//l2(同位角相等,两直线平行)
例 已知直线 被 所截,如图,
试判断 与 是否平行.并说明理由.
1
2
3
变1:条件弱化为∠1+∠2=180°,结论是否仍然成立?
4
变2:条件变为∠1=∠4,结论是否仍然成立?请说明理由.
变式2:
解:∵∠3=∠4(对顶角相等)
∵∠1=∠4
∴∠1=∠3
∴l1//l2(同位角相等,两直线平行)
变式1:
解:∵∠2+∠3=180°
∵∠1+∠2=180°
∴∠1=∠3
∴l1//l2(同位角相等,两直线平行)
若∠1=45°
,∠2=135
例题讲解
如图,已知∠ABD=∠ACE,BF、CG分别是∠ABD、∠ACE的平分线,请判断BF与CG是否平行,并说明理由。
A
B
C
D
E
F
G
解:
BF∥CG
1
2
∵BF、CG分别是∠ABD、∠ACE的平分线
∴ ∠1= ∠ABD,∠2= ∠ACE
∵
∠ABD=∠ACE
∴ ∠1=∠2
∴
BF∥CG( )
同位角相等,两直线平行
变式练习
如图,木工师傅用角尺画出工件边缘的两条垂线, 则这两条垂线就平行了.为什么呢
解
1
2
(同位角相等,两直线平行)
.
探究与发现——木工师傅为什么可以这样画?
推论:在同一平面内,垂直于同一条直线的两条直线互相平行.
几何语言:
∵a⊥c,b⊥c
∴a∥b
通过观察,我们知道图中一排旗杆都平行。 那么,任意找两根旗杆,请说说明一下它们为什么平行 你是如何作判断的 。
因为旗杆同垂直于经过旗杆与地面交点的直线,所以它们互相平行。
依据:在同一平面内,垂直于同一直线的两直线平行。
探究与发现——旗杆为什么平行
小明骑自行车从A地出发,沿正东方向前进至B处后,右转15°,沿直线向前行驶到C处(如图) .这时他想仍按正东方向行驶,那么他应怎样调整行驶方向?请画出他应继续行驶的路线,并说明理由.
活动—怎样调整行驶方向?
东
15°
1.调整后的路线和原路线所在的直线是什么位置关系?
2.如何理解“怎样调整行驶方向” ?
解: 向左拐 15°.如图
(同位角相等,两直线平行).
∵∠1=∠2=15°
∴AB//CD
画一画:已知直线AB和直线外一点C(如图).你能用一把三角尺过点C画AB的平行线吗?如果能,说明方法,并画出图形.
A
B
C
E
如图,直线CE就是所求的平行线.
D
想一想 如图,AB⊥CD于点B,AE与BF相交于点G,且FGE=60°,∠ABG=30°.判段AE与CD是否平行?
(1)平行线的判定方法。
(2)判定两直线平行的关键步骤:一找到截线与同位角,二说明同位角相等。
(3)注意说理过程的严密性。
(4)体会数学来源于生活,又应用于生活的用数学的思想。
A
B
C
D
E
F
若 AB⊥EF,CD⊥EF
则 AB∥ CD
∵
∴
E
1
2
A
B
C
D
F
∵ ∠.1=∠2
∴ AB∥CD
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
