浙教版七年级下册 3.1 同底数幂的乘法 课件(共18张PPT)
文档属性
| 名称 | 浙教版七年级下册 3.1 同底数幂的乘法 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-07-11 21:32:04 | ||
图片预览






文档简介
(共18张PPT)
§3.1 同底数幂的乘法 (2)
温 故
知 新
计算下列各式,并用幂的形式表示结果:
(1) 104×104 = _______________ ;
(2) 32×32×32 = _______________ ;
(3) a3·a3·a3·a3·a3 = _______________ ;
(4) ym·ym·ym·ym·ym·ym·ym = _______________________ .
【想一想】根据乘方的意义,将以上各式进行改写,于是可得:
(1) (2)
(3) (4)
104+4
=108
32+2+2
=36
a3+3+3+3+3
=a15
ym+m+m+m+m+m+m
=y7m
(104)2
=108
=104×2
(32)3
=36
=32×3
(a3)5
=a15
=a3×5
(ym)7
=y7m
=ym×7
【猜一猜】
(其中m , n都是正整数)
一 探
究 竟
【猜想】
(其中m , n都是正整数)
【证明】
n个
n个
幂的乘方法则:
归纳小结
幂的乘方,底数不变,指数相乘。
下式从左边到右边是怎样变化的?
幂的乘方法则:
底数不变
指数相乘
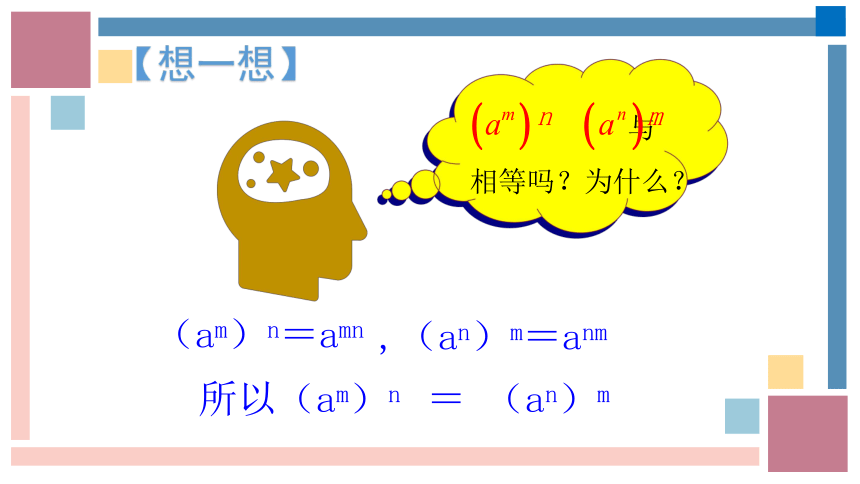
【想一想】
(am)n=amn
(an)m=anm
,
所以(am)n = (an)m
与 相等吗?为什么?
n
m
【例1】计算下列各式,并用幂的形式表示结果.
例 题
演 练
课内练习
作业题
2.
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
课内练习
二 探
究 竟
多重乘方可以重复运用上述法则:
(m ,n 都是正整数).
幂的乘方,底数不变,指数相乘.
幂的乘方性质:
(p是正整数).
归纳小结
4.
课内练习
二 探
究 竟
假设一个边长为a 的正方体魔方,现将它的边长变为原来的b 倍,所得的魔方的体积是多少?
你能发现有何运算规律吗?
积的乘方:
根据乘方的意义和乘法的运算律,计算:
(n是正整数).
(n是正整数).
【证明】
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
归纳小结
【想一想】
积的乘方:
(n是正整数).
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
当n 是正整数时,三个或三个以上因式的积的乘方,也具有这一性质吗?
推广:
巧 妙
应 用
计算:( )5×35
解法1: 原式=
解法2: 原式=
原来积的乘方法则可以逆用
即 anbn =(ab)n
你能计算吗?有没有简便方法?
课堂小结
1. 幂的乘方运算法则:底数不变,指数相乘
(am)n=amn(m,n都是正整数)
3. 同底数幂相乘法则、同底数幂相乘法则的联系与区别?
联系 区别
同底数幂相乘法则
幂的乘方法则
底数不变
底数不变
指数相乘
指数相加
2. 积的乘方法则:积的乘方等于把积的每个因式分别乘方,再把所得的幂相乘.
(ab)n =anbn (n为正整数)
§3.1 同底数幂的乘法 (2)
温 故
知 新
计算下列各式,并用幂的形式表示结果:
(1) 104×104 = _______________ ;
(2) 32×32×32 = _______________ ;
(3) a3·a3·a3·a3·a3 = _______________ ;
(4) ym·ym·ym·ym·ym·ym·ym = _______________________ .
【想一想】根据乘方的意义,将以上各式进行改写,于是可得:
(1) (2)
(3) (4)
104+4
=108
32+2+2
=36
a3+3+3+3+3
=a15
ym+m+m+m+m+m+m
=y7m
(104)2
=108
=104×2
(32)3
=36
=32×3
(a3)5
=a15
=a3×5
(ym)7
=y7m
=ym×7
【猜一猜】
(其中m , n都是正整数)
一 探
究 竟
【猜想】
(其中m , n都是正整数)
【证明】
n个
n个
幂的乘方法则:
归纳小结
幂的乘方,底数不变,指数相乘。
下式从左边到右边是怎样变化的?
幂的乘方法则:
底数不变
指数相乘
【想一想】
(am)n=amn
(an)m=anm
,
所以(am)n = (an)m
与 相等吗?为什么?
n
m
【例1】计算下列各式,并用幂的形式表示结果.
例 题
演 练
课内练习
作业题
2.
底数不变
指数相乘
指数相加
同底数幂相乘
幂的乘方
其中m , n都是正整数
课内练习
二 探
究 竟
多重乘方可以重复运用上述法则:
(m ,n 都是正整数).
幂的乘方,底数不变,指数相乘.
幂的乘方性质:
(p是正整数).
归纳小结
4.
课内练习
二 探
究 竟
假设一个边长为a 的正方体魔方,现将它的边长变为原来的b 倍,所得的魔方的体积是多少?
你能发现有何运算规律吗?
积的乘方:
根据乘方的意义和乘法的运算律,计算:
(n是正整数).
(n是正整数).
【证明】
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
归纳小结
【想一想】
积的乘方:
(n是正整数).
积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相乘.
当n 是正整数时,三个或三个以上因式的积的乘方,也具有这一性质吗?
推广:
巧 妙
应 用
计算:( )5×35
解法1: 原式=
解法2: 原式=
原来积的乘方法则可以逆用
即 anbn =(ab)n
你能计算吗?有没有简便方法?
课堂小结
1. 幂的乘方运算法则:底数不变,指数相乘
(am)n=amn(m,n都是正整数)
3. 同底数幂相乘法则、同底数幂相乘法则的联系与区别?
联系 区别
同底数幂相乘法则
幂的乘方法则
底数不变
底数不变
指数相乘
指数相加
2. 积的乘方法则:积的乘方等于把积的每个因式分别乘方,再把所得的幂相乘.
(ab)n =anbn (n为正整数)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
