第5章《分式》章节复习课件

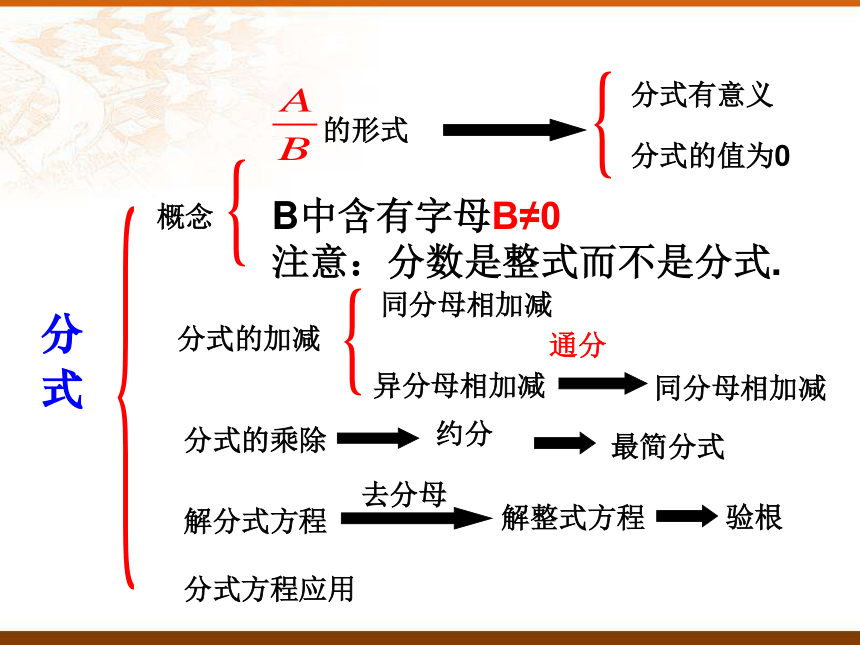
课件29张PPT。分式复习分式分式有意义分式的值为0同分母相加减异分母相加减概念 的形式B中含有字母B≠0
注意：分数是整式而不是分式. 分式的加减分式的乘除通分约分最简分式解分式方程去分母解整式方程验根分式方程应用同分母相加减考点一分式的概念问题典型例题解析【例1】 当a取何值时，分式
(1)值为零；(2)分式有意义?解： =
(1)当 时，有
即a=4或a=-1时，分式的值为零.(2)当2a-3=0即a=3/2时无意义.
故当a≠3/2时，分式有意义.思考变题：当a为何值时， 的值
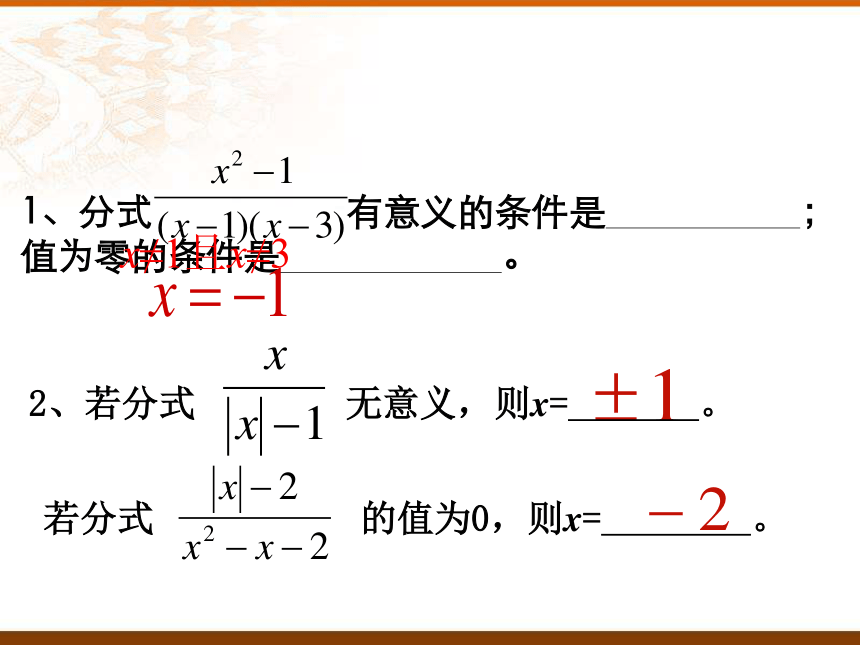
(1)为正；(2)为零.1、分式 有意义的条件是 ；值为零的条件是 。x≠1且x≠3 2、若分式 无意义，则x= 。若分式 的值为0，则x= 。
3、在代数式 、 、 、 中，分式共有
(A)1个 (B)2个 (C)3个 (D)4个4、当x<0时，化简 的结果是（ ）
(A) – 2 (B) 0 (C)2 (D)无法确定考点二分式的基本性质分式的符号法则：
分式的分子、分母与分式本身的符号，
改变其中任意两个，分式的值不变.【例2】 不改变分式的值，先把分式：
的分子、分母的最高次项系数化为正整数，然后约分， 化成最简分式.
解：原式= =
= =
=
=
典型例题解析AD课时训练分式约分的主要步骤是：
1、把分式的分子与分母分解因式。
2、然后约去分子与分母的公因式.
约分一般是将一个分式化为最简分式，将分式约分所得的结果有时可能是整式. 分式的乘法法则：
分式乘以分式，用分子的积做积的分子，分母的积做积的分母. 1、下列等式从左到右的变形一定正确的是（ ）2、写出一个分母含有两项且能够约分的分式 。课时训练A（2）不改变分式的值，使它的分子、分母的最高次项的系数都是正数，则=考点三分式的运算分式的除法法则：分式除以分式，把除式的分子、分
母颠倒位置，与被除式相乘. 分式的乘方法则：分式乘方是将分子、分母各自乘方。
同分母的分式加减法法则：同分母分式相加减分母不变
，把分子相加减，式子表示为： ± = 异分母的分式加减法法则：异分母的分式相加减先
通分，变为同分母的分式，然后相加减，式子表示为：
± = ± = 【例4】 计算：(1) ；
(2) ；
(3)［( )( )-3］÷( ).解：(1)原式=
=
=
典型例题解析(2)原式=
= =
=典型例题解析(3)原式=［ ］÷( )
=［ ］
=( ) =
= =【例5】 (2013年·山西省)化简求值：
( ) ÷ ，其中a满足：a2-2a-1=0. 解：原式=［ ］×
= × = ×
= =典型例题解析又∵a2+2a-1=0，
∴a2+2a=1
∴原式=1【例6】 化简： + + + .
解：原式=
=
=
=
典型例题解析计算或化简xxxx-+--+11211)1()2(
)3(考点四分式方程及应用分式方程去分母整式方程验根例 解方程：解：两边都乘以，并整理得；解得检验：x=1是原方程的根，x=2是增根∴原方程的根是x=1解方程：无解列分式方程解应用题的一般步骤1.审:分析题意,找出研究对象，建立等量关系.2.设:选择恰当的未知数,注意单位.3.列:根据等量关系正确列出方程.4.解:认真仔细.5.验:有二次检验.6.答:不要忘记写.(1)一件工作甲单独做要m小时完成，乙单独做要n小时完成，如果两人合做，完成这
件工作的时间是 小时；　(2)某食堂有米m公斤，原计划每天用粮a公斤，现在每天节约用粮b公斤，则可以比原计划
多用天数是 ;　解:设江水每小时的流速是x千米，根据题意得：2.已知轮船在静水中每小时行20千米，如果此船在某江中顺流航行72千米所用的时间与逆流航行48千米所用的时间相同，那么此江水每小时的流速是多少千米?当x 时，分式 有意义。 3.计算： = . 4.在分式① ,② ,③ ,④ 中 ，最
简分式的个数是 ( )
A.1 B.2 C.3 D.4≠12. (2013年·南京)计算： = . B1课时训练3.(2004年·杭州)甲、乙两人分别从两地同时出发，
若相向而行，则a小时相遇；若同向而行，则b小时
甲追上乙，那么甲的速度是乙速度的 ( )
A. B. C. D.
课时训练(2004年·上海)函数 的定义域是 .2.(2004 年·重庆)若分式 的值为零，则x
的值为 ( )
A.3 B.3或-3 C.-3 D.0x>-1CC课时训练5.(2012年·青海)化简： 4.（2013年· 黄冈）化简： 的结果是： 。感悟与收获这堂课你收获了什么？