2022-2023学年浙教版数学七年级下册5.2 分式的基本性质 课件(共25张PPT)
文档属性
| 名称 | 2022-2023学年浙教版数学七年级下册5.2 分式的基本性质 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1016.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-08-13 10:01:18 | ||
图片预览







文档简介
(共25张PPT)
浙教版数学 七年级下
5.2 分式的基本性质
学习目标
1. 掌握分式的基本性质;
2. 理解约分的概念,并能对分式约分.
这三个分数之间有何数量关系? 你的依据是什么?
分数的分子与分母都乘以(或除以)同一个不等于零的数,分数的值不变.
类 比 猜 想
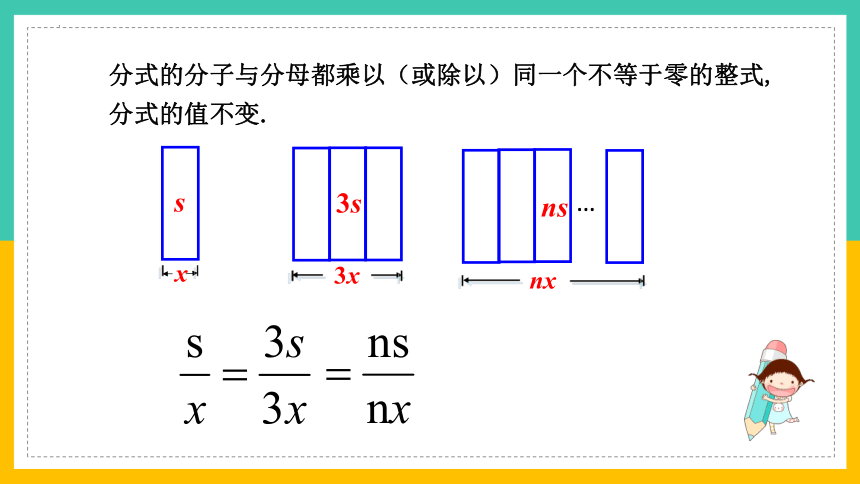
分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
s
x
3s
3x
…
ns
nx
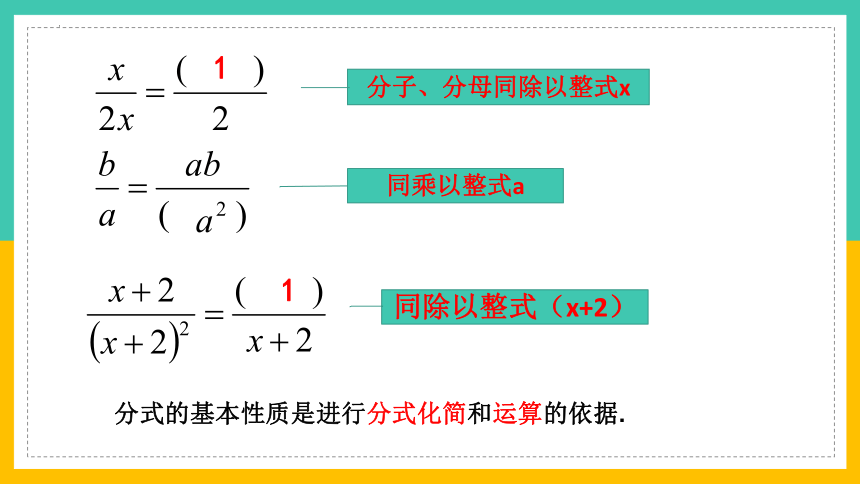
1
分子、分母同除以整式x
同乘以整式a
1
同除以整式(x+2)
分式的基本性质是进行分式化简和运算的依据.
你认为分式 与 相等吗?
与 呢?
相等, 两边同时除以a可得到 .
相等, 两边同时乘以n可得到 .
结论:分式的分子、分母都乘(或除以)同一个不等于零的整式,分式的值不变.
分式的基本性质:
分式的分子、分母都乘(或除以)同一个不等于零的整式,分式的值不变.
, (其中M是不等于零的整式).
填空(在括号内填入适当的整式,使分式的值不变):
(1) ;(2) ;(3) .
解:(1)∵ ,故填1;
(2) ∵ ,故填x+2 ;
(3) ∵ ,故填a.
不改变分式的值,把下列分式的分子与分母中各项的系数都 化为整数.
(1) ; (2) .
解:(1) ;
(2) .
做一做
系数化为整数
当系数是分数时,分式的分子、分母都乘以每一项系数的分母的最小公倍数;
当系数是小数时,一般情况下,分式的分子分母都乘以10的倍数.
针对练习
不改变分式的值,把下列分式的分子与分母中各项的系数都 化为整数.
(1) ; (2) .
解:(1)原式= ;(2)原式= .
分式中负号的位置变化
, , .
不改变分式的值,使下列分式的分子与分母都不含“-”号.
(1) ;(2) ;(3) .
解:(1)原式= ;
(2)原式= ;
(3)原式= .
活动探究
分式的变号法则
针对练习
不改变分式的值,使下列分式的分子与分母的最高次项的系数
都化为正数.
(1) ;(2) .
解:(1)原式= ;
(2)原式= .
1、计算: = .
2、观察下列式子与第1题的异同,试一试计算:
(1) ; (2) .
解:(1) ;
(2) .
活动探究
分式的约分
例1 化简下列各式:
(1) ; (2) .
解:(1) ;
根据什么?
(2) .
运用分式的基本性质,把一个分式中分子和分母的公因式约去,叫做分式的约分.
约分要约去分子、分母所有的公因式.
分子、分母没有公因式的分式叫做最简分式.
把分式化为最简分式的一般步骤:
2.确定分子、分母的公因式;
1.分式的分子、分母能分解因式的先把分式的分子、分母分解因式;
3.约去分子、分母的公因式.
问题:如何找分子分母的公因式?
(1)系数:
最大公约数
(2)字母:
相同字母取最低次幂
先分解因式,再找公因式
(3)多项式:
针对练习
约分:
(1) ; (2) ;
(3) ; (4) .
解:(1) ;
(2) ;
(3) ;
(4) .
拓展应用
例2 已知x-3y=0,求分式 的值.
解:由已知x-3y=0,得x=3y.
∴
=
=
= .
你还有不同的解法吗?
用分式表示下列各式的商,并约分.
(1) ;
(2) .
解:(1)原式= ;
(2) .
利用分式的意义和分式约分,进行多项式除法的步骤:
1、把两个多项式相除表示成分式的形式;
2、把分子、分母分别进行因式分解;
3、约分,用最简分式或整式表示所求的商.
例3 计算:
(1) ;(2) .
解:(1)
=
=
=-(2x+3)
=- 2x-3;
(2)
=
=
=
= .
1、下列各式中,从左到右变形正确的是( )
A、 B、 C、 D、
C
2、将分式 中分子与分母的各项系数都化成整数,正确的是( )
A、 B、 C、 D、
A
3、若把分式 中的x和y都扩大3倍,且x+y≠0,那么分式的值( )
A.不变 B.扩大3倍 C.缩小3倍 D.缩6倍
A
2、约分:把一个分式中分子和分母的公因式约去,叫做分式的约分.
3、最简分式:分子、分母没有公因式的分式叫做最简分式.
1、分式的基本性质:分式的分子、分母都乘(或除以)同一个不等于零的整式,分式的值不变.
4、分式基本性质的应用:
(1)求值;(2)多项式除法.
本节课我们学习了:
浙教版数学 七年级下
5.2 分式的基本性质
学习目标
1. 掌握分式的基本性质;
2. 理解约分的概念,并能对分式约分.
这三个分数之间有何数量关系? 你的依据是什么?
分数的分子与分母都乘以(或除以)同一个不等于零的数,分数的值不变.
类 比 猜 想
分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
s
x
3s
3x
…
ns
nx
1
分子、分母同除以整式x
同乘以整式a
1
同除以整式(x+2)
分式的基本性质是进行分式化简和运算的依据.
你认为分式 与 相等吗?
与 呢?
相等, 两边同时除以a可得到 .
相等, 两边同时乘以n可得到 .
结论:分式的分子、分母都乘(或除以)同一个不等于零的整式,分式的值不变.
分式的基本性质:
分式的分子、分母都乘(或除以)同一个不等于零的整式,分式的值不变.
, (其中M是不等于零的整式).
填空(在括号内填入适当的整式,使分式的值不变):
(1) ;(2) ;(3) .
解:(1)∵ ,故填1;
(2) ∵ ,故填x+2 ;
(3) ∵ ,故填a.
不改变分式的值,把下列分式的分子与分母中各项的系数都 化为整数.
(1) ; (2) .
解:(1) ;
(2) .
做一做
系数化为整数
当系数是分数时,分式的分子、分母都乘以每一项系数的分母的最小公倍数;
当系数是小数时,一般情况下,分式的分子分母都乘以10的倍数.
针对练习
不改变分式的值,把下列分式的分子与分母中各项的系数都 化为整数.
(1) ; (2) .
解:(1)原式= ;(2)原式= .
分式中负号的位置变化
, , .
不改变分式的值,使下列分式的分子与分母都不含“-”号.
(1) ;(2) ;(3) .
解:(1)原式= ;
(2)原式= ;
(3)原式= .
活动探究
分式的变号法则
针对练习
不改变分式的值,使下列分式的分子与分母的最高次项的系数
都化为正数.
(1) ;(2) .
解:(1)原式= ;
(2)原式= .
1、计算: = .
2、观察下列式子与第1题的异同,试一试计算:
(1) ; (2) .
解:(1) ;
(2) .
活动探究
分式的约分
例1 化简下列各式:
(1) ; (2) .
解:(1) ;
根据什么?
(2) .
运用分式的基本性质,把一个分式中分子和分母的公因式约去,叫做分式的约分.
约分要约去分子、分母所有的公因式.
分子、分母没有公因式的分式叫做最简分式.
把分式化为最简分式的一般步骤:
2.确定分子、分母的公因式;
1.分式的分子、分母能分解因式的先把分式的分子、分母分解因式;
3.约去分子、分母的公因式.
问题:如何找分子分母的公因式?
(1)系数:
最大公约数
(2)字母:
相同字母取最低次幂
先分解因式,再找公因式
(3)多项式:
针对练习
约分:
(1) ; (2) ;
(3) ; (4) .
解:(1) ;
(2) ;
(3) ;
(4) .
拓展应用
例2 已知x-3y=0,求分式 的值.
解:由已知x-3y=0,得x=3y.
∴
=
=
= .
你还有不同的解法吗?
用分式表示下列各式的商,并约分.
(1) ;
(2) .
解:(1)原式= ;
(2) .
利用分式的意义和分式约分,进行多项式除法的步骤:
1、把两个多项式相除表示成分式的形式;
2、把分子、分母分别进行因式分解;
3、约分,用最简分式或整式表示所求的商.
例3 计算:
(1) ;(2) .
解:(1)
=
=
=-(2x+3)
=- 2x-3;
(2)
=
=
=
= .
1、下列各式中,从左到右变形正确的是( )
A、 B、 C、 D、
C
2、将分式 中分子与分母的各项系数都化成整数,正确的是( )
A、 B、 C、 D、
A
3、若把分式 中的x和y都扩大3倍,且x+y≠0,那么分式的值( )
A.不变 B.扩大3倍 C.缩小3倍 D.缩6倍
A
2、约分:把一个分式中分子和分母的公因式约去,叫做分式的约分.
3、最简分式:分子、分母没有公因式的分式叫做最简分式.
1、分式的基本性质:分式的分子、分母都乘(或除以)同一个不等于零的整式,分式的值不变.
4、分式基本性质的应用:
(1)求值;(2)多项式除法.
本节课我们学习了:
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
