5.1同底数幂的乘法(2)

课件27张PPT。同底数幂的乘法回顾一下吧a·a·a·······an个= an同底数幂相乘的法则：am·an = a m+n（m,n是正整数）乘方的意义：同底数幂相乘，底数不变，指数相加。猜想足球的体积是乒乓球的几倍？若已知足球的半径是10cm，乒乓球的半径是2cm，那么能不能算一算足球与乒乓球的体积，其中球体的体积公式是∴= 125= 5= 53 从计算的结果我们看出，球体的体积与半径的大小有着紧密的联系，如果甲球的半径是乙球的n倍，那么甲球的体积是乙球的体积的n3倍地球、木星、太阳可以近似看成球体，木星、太阳的半径分别约为地球的10倍和102倍，他们的体积约是地球的多少倍？地球木星太阳木星的体积是地球的体积的103倍，而太阳的体积则是地球的体积的(102)3你知道(102)3到底是多少倍吗？猜想一下，并说明你的理由 半径扩大的倍数与体积扩大的倍数哪个变化更大？这节课我们共同研究“幂的乘方”。计算下列各式，并说明理由
（1）（102）3 （2）（34）2
（3）（a3）5 （4）（am）n解（1）（102）3＝102×102×102（根据幂的意义）
＝102＋2＋2（根据同底幂相乘法则）
＝102×3
（2）（34）2＝34×34＝34＋4＝34×2=38
（3）（a3）5＝a3·a3·a3·a3·a3＝a3＋3＋3＋3＋3
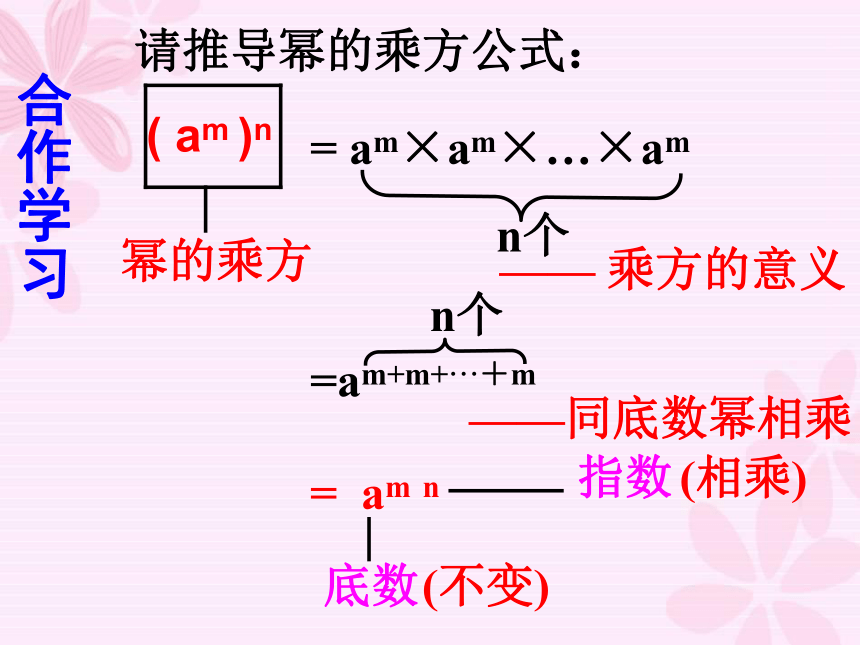
＝a3×5＝a15试一试,做一做 ( am )n= am×am×…×am=am+m+···＋mn个n个= am n底数(不变)(相乘)合作学习请推导幂的乘方公式：—— 乘方的意义——同底数幂相乘幂的乘方法则：这就是说，例1 计算
1) (107)3 2) (a4)8
3) (－5 3)3 4) 〔(－3)6〕2
5) －(y4)3 6) (a-b)3 2
解:= 10 7×3= 10212) (a4)83) (－53)34)〔(－3)6〕2= a 4×8= a 32= － 5 3×3=－5 9= (36)2= 3 121) (107)3运用新知 5) － (y4)3 =－ y4×3 =－y12(a-b)3 ×2 =(a-b)6抢答：⑵ (a3)6⑶ - (x5)2⑴ x4·x3⑷ [(x+y)3]4=x7=(x+y)12=a18=-x10 如果这个正方体的棱长是 42 cm,那么它的体积是　　　cm3. 你知道 (42)3 是多少个 4 相乘吗?你知道吗？(42)3练习：(口答)
1) (a3)4
2) a3·a4
3) ( y4)2
4) y4 · y 2
5) ( b m )2
6) b m · b 2= a7= b2m= b2+m= a12= y8= y6幂的乘方同底数幂相乘巩固新知由此你能对两个法则进行比较吗？你有什么发现？幂的乘方法则：其中m , n都是正整数同底数幂的乘法法则：底数不变指数相乘指数相加其中m , n都是正整数 下面的计算对吗?如果不对 ,
应怎样改正?
(43) 5 = 4 8
（-28）3= （-2）24
(-3) 5 3 = -315
(52 )4 ×5 = 58
巩固新知（×） 415（×） 224（√） （×） 59想一想:2.说出下面每一步计算理由,并将它们填入括号内:
(p2)3.(p5)2
=p6.p10 ( )
=p6+10 ( )
=p16幂的乘方法则同底数幂的乘法法则练一练:1.填空:(用幂的形式表示结果)
(a3)4= ; a3.a4 = ;
(bm)2= ; x3+x3= ;
-(-y2)4= ; (x2n)2n= .2.计算下列各式,结果用幂的形式表示:
(73)4 (2) [(-10)3]5 (3) (a2)3.a4
(4) (b3)2+(b2)3 (5) -(-y2)5 (6) [(x+1)3]4a12a7b2m2x3-y8 解: ⑴x2·x4+(x3)2 =⑴x2·x4+(x3)2 ⑵(a3)3· (a4)3x2+4+x3×2=x6+x6=2 x6⑵(a3)3· (a4)3=a3×3·a4×3=a9·a12=a9+12=a21思考：和相等吗?（am）n与（an）m相等吗？为什么？（am）n=（an）m思考题：1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672动脑筋！（ ）变一变，试试看
⑴ 85＝2⑵ a12=(a3)( )
=(a2)( )
= a3 ·a( )注：幂运算性质 均可逆向应用am·an=am+n(am) n=am n15469探索(我相信你一定会成功）⑴ 22与32⑶ 340与 430哪个
大呢？⑵ 43与53想： 340＝（ ）在255，344，433，522，这四个幂的数值中，最大的一个是_______ 344你玩过魔方吗？ 魔方是匈牙利建筑师鲁比克
发明的一种智力玩具。 ★设组成魔方的每一个小立方块
（我们称它为基本单元）的棱长
为1，那么一个魔方的体积
是 。33探究活动你知道魔方的结构吗？探究活动★ 以这种魔方为基本单元做一个
大魔方，那么这个大魔方的体
积可以怎么表示呢？★ 如果再以这个大魔方为基本单
元做一个更大的魔方呢？( 3 2)3( 3 3)3本节课的收获？？相加相乘不变
不变想一想：同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点？