【四清导航】2015春七年级数学下册(浙教版,A本)同步习题精讲课件:第1章+平行线(共21张PPT)
文档属性
| 名称 | 【四清导航】2015春七年级数学下册(浙教版,A本)同步习题精讲课件:第1章+平行线(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-31 11:43:38 | ||
图片预览




文档简介
课件21张PPT。
(A本)第1章 平行线 1.1 平行线
1.(4分)下列说法中,正确的是( )
A.若两条直线不相交,则它们平行
B.若两条直线不平行,则它们相交
C.若两条线段平行,则它们不相交
D.若两条线段不相交,则它们平行
2.(4分)下列表示两条直线平行的方法正确的是( )
A.a∥A B.AB∥cd
C.A∥B D.a∥b
3.(4分)在同一平面内有三条直线,其中只有两条是平行线,那么交点共有( )
A.0个 B.1个
C.2个 D.3个
4.(4分)如图,过点C作线段AB的平行线,下列说法正确的是( )
A.不能作出 B.只能作一条
C.能作两条 D.能作无数条
5.(4分)下列说法不正确的是( )
A.过任意一点P可作已知直线l的一条平行线
B.同一平面内的两条不重合不相交的直线是平行线
C.过直线外一点只能画一条直线与已知直线平行
D.平行于同一条直线的两条直线平行
第1章 平行线 1.1 平行线 6.(4分)把下图中互相平行的线段一一写出来:
GH∥MN,EF∥AB,CD∥PQ__.
7.(6分)在同一平面内,直线l1与l2满足下列条件:
(1)l1与l2没有公共点,则l1与l2__ __;
(2)l1与l2有且只有一个公共点,则l1与l2__ __;
(3)l1与l2有两个公共点,则l1与l2__ __.
8.(4分)如图所示的长方体,用符号表示下列棱的位置关系:A1B1____AB,AA1____BB1, A1D1____C1D1,AD____BC.
第1章 平行线 1.1 平行线
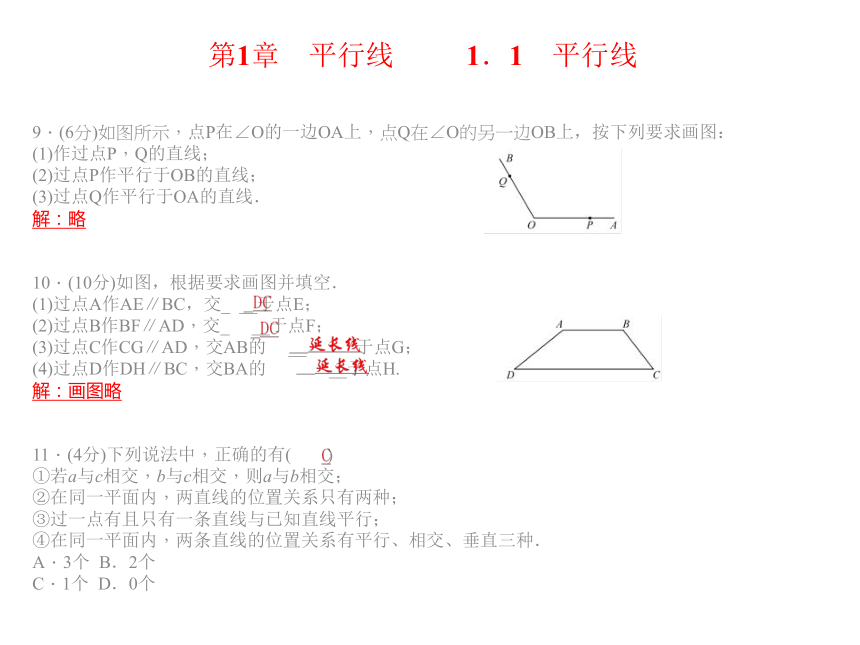
9.(6分)如图所示,点P在∠O的一边OA上,点Q在∠O的另一边OB上,按下列要求画图:
(1)作过点P,Q的直线;
(2)过点P作平行于OB的直线;
(3)过点Q作平行于OA的直线.
解:略
??
?
10.(10分)如图,根据要求画图并填空.
(1)过点A作AE∥BC,交_ __于点E;
(2)过点B作BF∥AD,交_ __于点F;
(3)过点C作CG∥AD,交AB的 __ 于点G;
(4)过点D作DH∥BC,交BA的 __于点H.
解:画图略
??
?
11.(4分)下列说法中,正确的有( )
①若a与c相交,b与c相交,则a与b相交;
②在同一平面内,两直线的位置关系只有两种;
③过一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
A.3个 B.2个
C.1个 D.0个
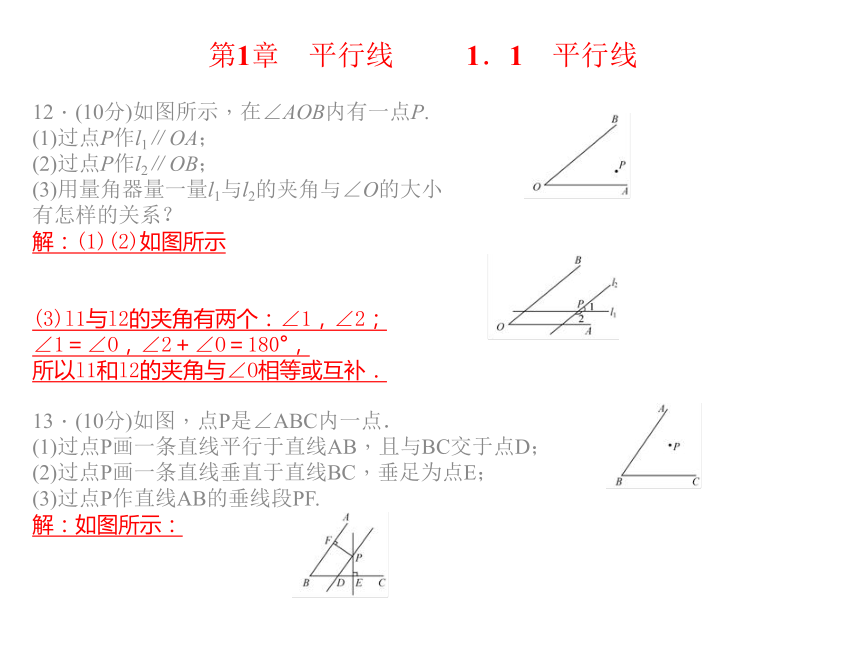
第1章 平行线 1.1 平行线 12.(10分)如图所示,在∠AOB内有一点P.
(1)过点P作l1∥OA;
(2)过点P作l2∥OB;
(3)用量角器量一量l1与l2的夹角与∠O的大小
有怎样的关系?
解:(1)(2)如图所示
(3)l1与l2的夹角有两个:∠1,∠2;
∠1=∠O,∠2+∠O=180°,
所以l1和l2的夹角与∠O相等或互补.
?
13.(10分)如图,点P是∠ABC内一点.
(1)过点P画一条直线平行于直线AB,且与BC交于点D;
(2)过点P画一条直线垂直于直线BC,垂足为点E;
(3)过点P作直线AB的垂线段PF.
解:如图所示:
?
?
第1章 平行线 1.1 平行线 14.(10分)如图所示,在写艺术字时,常常运用画“平行线段”这种基本作图方法,此图是在书写字母“M”.
(1)请从正面,上面,右侧三个不同方向上各找出一组平行线段,并用字母表示出来;
(2)EF与A′B′有何位置关系,CC′与DH有何位置关系?
解:(1)答案不唯一,如正面:C′⊥DHAB∥EF;上面:A′B′∥AB;右侧DD′∥HR
(2)EF∥A′B′,C
?
?
?
?
?
?
?
【综合运用】
15.(16分)如图所示,点D,E是线段AC的三等分点.
(1)过点D作DF∥BC交AB于点F,过点E作EG∥BC交AB于点G;
(2)量出AF,FG,GB的长度(精确到0.1 cm),你有什么发现?
(3)量出FD,GE,BC的长度(精确到0.1 cm),你有什么发现?
(4)根据(3)中发现的规律,若FD=1.5 cm,则EG=__3__ cm,BC=__4.5__ cm.
解:(1)略 (2)量线段长度略,AF=FG=GB
(3)量线段长度略,FD∶GE∶BC=1∶2∶3或FD+BC=2GE (4)3 4.5
?
1.3 平行线的判定 第1课时 平行线的判定(一) 1.(4分)下列说法中正确的是( )
A.两条不相交的直线叫平行线
B.一条直线的平行线有且只有一条
C.同位角相等,两直线平行
D.若两条直线不相交,则它们平行
2.(4分)如图所示,∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
3.(4分)已知同一平面内有三条直线l1,l2,l3,如果l1⊥l2,l2⊥l3,则l1与l3的位置关系是( )
A.平行 B.相交
C.垂直 D.以上都不对
4.(4分)如图所示,直线l1和l2被直线l所截,下列说法中正确的是( )
A.因为∠1和∠2互补,所以l1∥l2
B.当∠2=∠3时,l1∥l2
C.当∠1=∠2时,l1∥l2
D.如果∠1=∠3,那么l1∥l2
5.(4分)如图所示,由∠2=∠1,可以得出的结论是( )
A.AD∥CEB.AD∥BC
C.FG∥CED.FG∥BC
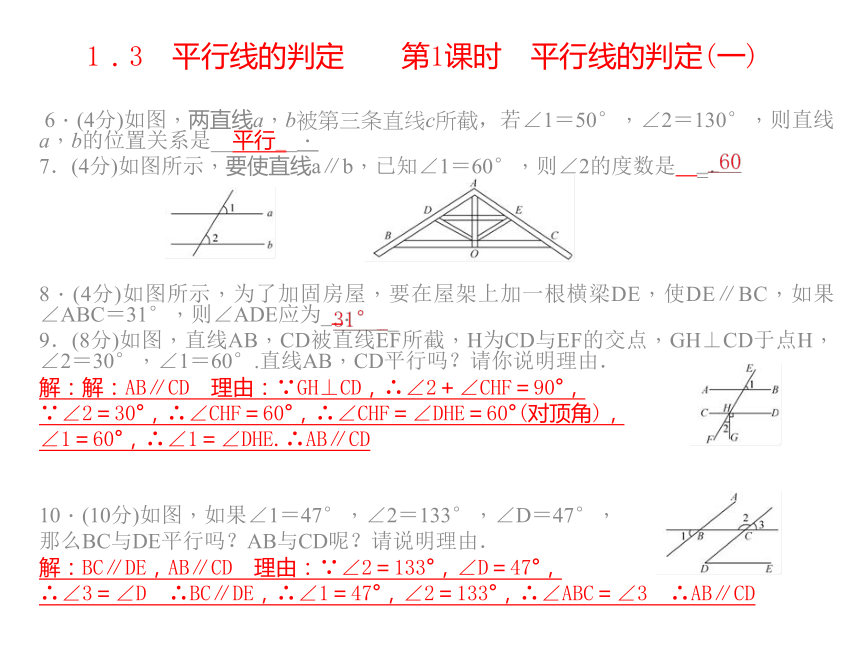
1.3 平行线的判定 第1课时 平行线的判定(一) 6.(4分)如图,两直线a,b被第三条直线c所截,若∠1=50°,∠2=130°,则直线a,b的位置关系是__平行__.
7.(4分)如图所示,要使直线a∥b,已知∠1=60°,则∠2的度数是 _.
8.(4分)如图所示,为了加固房屋,要在屋架上加一根横梁DE,使DE∥BC,如果∠ABC=31°,则∠ADE应为__.
9.(8分)如图,直线AB,CD被直线EF所截,H为CD与EF的交点,GH⊥CD于点H,∠2=30°,∠1=60°.直线AB,CD平行吗?请你说明理由.
解:解:AB∥CD 理由:∵GH⊥CD,∴∠2+∠CHF=90°,
∵∠2=30°,∴∠CHF=60°,∴∠CHF=∠DHE=60°(对顶角),
∠1=60°,∴∠1=∠DHE.∴AB∥CD
?
?
10.(10分)如图,如果∠1=47°,∠2=133°,∠D=47°,
那么BC与DE平行吗?AB与CD呢?请说明理由.
解:BC∥DE,AB∥CD 理由:∵∠2=133°,∠D=47°,
∴∠3=∠D ∴BC∥DE,∴∠1=47°,∠2=133°,∴∠ABC=∠3 ∴AB∥CD
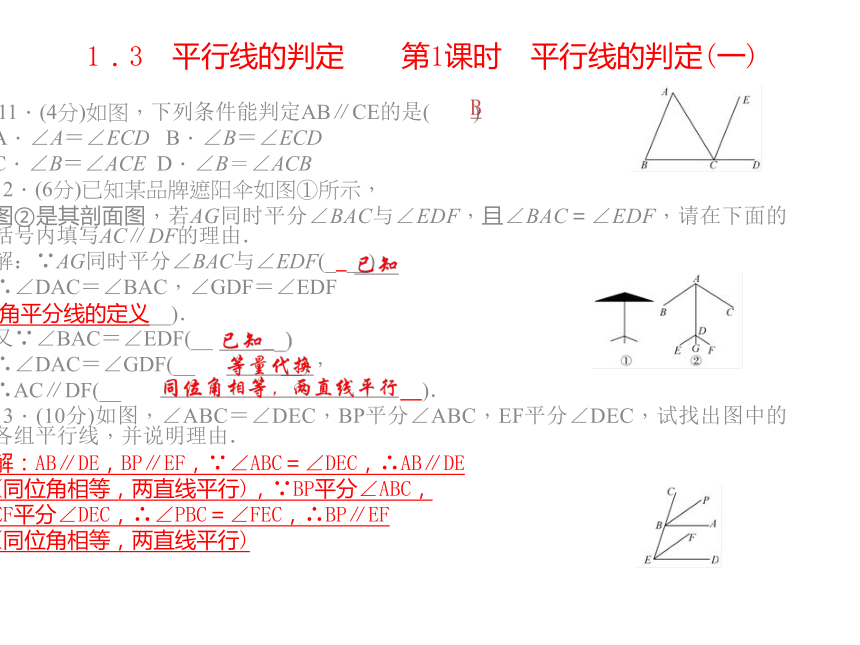
1.3 平行线的判定 第1课时 平行线的判定(一) 11.(4分)如图,下列条件能判定AB∥CE的是( )
A.∠A=∠ECD B.∠B=∠ECD
C.∠B=∠ACE D.∠B=∠ACB
12.(6分)已知某品牌遮阳伞如图①所示,
图②是其剖面图,若AG同时平分∠BAC与∠EDF,且∠BAC=∠EDF,请在下面的括号内填写AC∥DF的理由.
解:∵AG同时平分∠BAC与∠EDF(____),
∴∠DAC=∠BAC,∠GDF=∠EDF
(角平分线的定义__).
又∵∠BAC=∠EDF(__ ,
∴∠DAC=∠GDF(__ __),
∴AC∥DF(__ __).
13.(10分)如图,∠ABC=∠DEC,BP平分∠ABC,EF平分∠DEC,试找出图中的各组平行线,并说明理由.
解:AB∥DE,BP∥EF,∵∠ABC=∠DEC,∴AB∥DE
(同位角相等,两直线平行),∵BP平分∠ABC,
EF平分∠DEC,∴∠PBC=∠FEC,∴BP∥EF
(同位角相等,两直线平行)
?
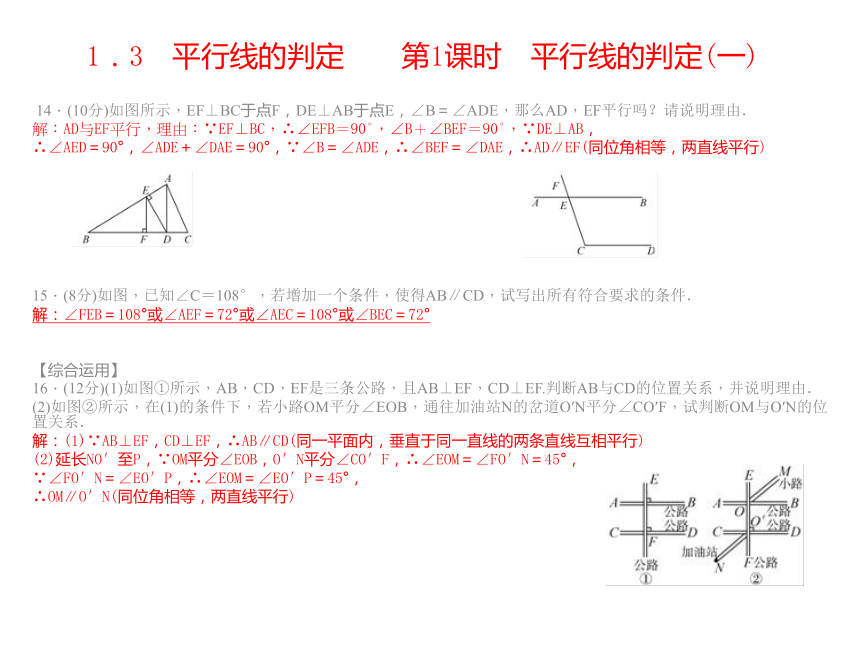
1.3 平行线的判定 第1课时 平行线的判定(一) 14.(10分)如图所示,EF⊥BC于点F,DE⊥AB于点E,∠B=∠ADE,那么AD,EF平行吗?请说明理由.
解:AD与EF平行,理由:∵EF⊥BC,∴∠EFB=90°,∠B+∠BEF=90°,∵DE⊥AB,
∴∠AED=90°,∠ADE+∠DAE=90°,∵∠B=∠ADE,∴∠BEF=∠DAE,∴AD∥EF(同位角相等,两直线平行)
?
15.(8分)如图,已知∠C=108°,若增加一个条件,使得AB∥CD,试写出所有符合要求的条件.
解:∠FEB=108°或∠AEF=72°或∠AEC=108°或∠BEC=72°
???
【综合运用】
16.(12分)(1)如图①所示,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由.
(2)如图②所示,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N的位置关系.
解:(1)∵AB⊥EF,CD⊥EF,∴AB∥CD(同一平面内,垂直于同一直线的两条直线互相平行)
(2)延长NO′至P,∵OM平分∠EOB,O′N平分∠CO′F,∴∠EOM=∠FO′N=45°,
∵∠FO′N=∠EO′P,∴∠EOM=∠EO′P=45°,
∴OM∥O′N(同位角相等,两直线平行)
1.4 平行线的性质 第1课时 平行线的性质(一) 1.(4分)如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=60°,则∠2的度数( )
A.50° B.45° C.35° D.30°
2.(4分)如图,已知直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数为( )
A.30° B.60° C.120° D.150°
3.(4分)如图,AC∥DF,AB∥EF,点D,E分别在AB,AC上,若∠2=50°,则∠1的大小是( )
A.30° B.40° C.50° D.60°
4.(4分)如图所示,AB∥CD,直线AF分别交AB,CD于点A,C,CE平分∠DCF,∠1=100°,则∠2的度数为( )
A.40° B.50° C.60° D.70°
5.(4分)两条平行线被第三条直线所截,则一对同位角的角平分线( )
A.相交 B.平行 C.垂直 D.不能确定
1.4 平行线的性质 第1课时 平行线的性质(一)
6.(4分)已知直线a∥b,若∠1=40°50′,则∠2=__.
7.(4分)如图,直尺一边AB与量角器的零刻度线CD平行,若量角器的一条刻度线OF的读数为70°,OF与AB交于点E,那么∠AEF=____度.
8.(6分)如图所示,已知AB∥DE,EF∥BC,∠B=45°,求∠E的度数.
解:∵AB∥DE(已知),
∴∠B=∠COE(__ __).
∵EF∥BC(已知),
∴∠BOD=∠E(__.
又∵∠BOD=∠COE(__,
∴∠E=∠B=45°(等量代换).
9.(6分)完成下列推理:
如图所示,已知∠1=36°,∠C=74°,∠B=36°,求∠2的度数.
解:因为∠1=__ =36°,所以__ __(同位角相等,两直线平行).
所以∠2=__ 两直线平行,同位角相等).
10.(10分)如图所示,已知∠1=∠2,∠3=90°,求∠4的度数.
解:∵∠1=∠2,∴a∥b(同位角相等,两直线平行),∴∠3=∠4(
两直线平行,同位角相等),∵∠3=90°,∴∠4=90°
?
?
?
?
1.4 平行线的性质 第1课时 平行线的性质(一)
11.(4分)如图所示,∠AOB的两边OA,OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则∠DEB的度数是( )
A.35° B.70° C.110° D.120°
12.(4分)如图所示,直线a,b被直线c所截,构成8个角,若a∥b,则这8个角中与∠1相等的角共有___个(不含∠1).
13.(10分)如图所示,已知点D,E,F,分别在AB,AC,BC上,DE∥BC,EF∥AB,则∠1=∠2吗?为什么?
解:∠1=∠2,理由:∵DE∥BC,∴∠1=∠B(两直线平行,同位角相等),∵EF∥AB,∴∠B=∠2(两直线平行,同位角相等),∴∠1=∠2
?
?
14.(10分)如图所示,直线a∥b,∠1=54°,那么∠2,∠3,∠4各是多少度?
解:∠2=54°,∠3=126°,∠4=54°
?
?
?
?
?
?
?
1.4 平行线的性质 第1课时 平行线的性质(一)
15.(10分)如图,EF⊥AB,EF⊥CD,直线GH与AB,CD相交,试说明∠1+∠2=180°.
解:∵EF⊥AB,EF⊥CD,∴AB∥CD(同一平面内,垂直于同一条直线的两条直线互相平行),∵AB∥CD,∴∠1=∠5(两直线平行,同位角相等),∵∠5+∠2=180°,∴∠1+∠2=180°
?
?
?
?
?
?
【综合运用】
16.(12分)如图所示,水渠的两岸互相平行,修渠时要求拐弯处∠1=110°,那么∠2应等于多少度?为什么?
解:∠2=110°,理由:连接BE并延长至G点,∵AB∥DE,∴∠ABE=∠DEG(两直线平行,同位角相等).∵EF∥BC,∴∠CBE=∠FEG(两直线平行,同位角相等),∵∠1=∠ABE+∠CBE=110°,∴∠2=∠DEG+∠FEG=110°
?
专题一 与平行线的判定和性质有关的计算与证明
一 与平行线的判定有关的计算和证明
教材母题?(教材P11作业题第3题)
如图,已知直线l1,l2被直线AB所截,AC⊥l2于点C.若∠1=50°,∠2=40°,则l1与l2平行吗?请说明理由.
解:l1∥l2,理由:∵∠1=50°,∠2=40°,∴∠1+∠2=90°,
∴AC⊥l1,又∵AC⊥l2,∴l1∥l2
?
?【思想方法】 平行线的判定可用“由角定线”这四个字来概括,即通过说明
某些角相等(或互补)来判定两直线平行.
变形1 如图1,已知直线a,b,c,d,其中c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2等于( )
A.60° B.50° C.40° D.30°
变形2 如图2,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=__.
变形3 如图3,∠1+∠2=180°,∠3=100°,则∠4等于( )
A.70° B.80° C.90° D.100°
变形4 如图4,∠1=∠2,∠3=40°,则∠4等于( )
A.120° B.130° C.140° D.40°
专题一 与平行线的判定和性质有关的计算与证明
变形5 如图,已知∠1的度数是它的补角的3倍,∠2=45°,那么AB∥CD吗?为什么?
解:AB∥CD,理由:∵∠1的度数是它的补角的3倍,∴∠1=135°,∴∠MNC=45°,∴∠2=∠MNC,∴AB∥CD(同位角相等,两直线平行)
?
?
?
变形6 如图所示,已知∠1=50°,∠2=130°,∠4=50°,∠6=130°,试说明a∥b,b∥c,d∥e,a∥c.
证明:∵∠1=50°,∠2=130°,∠1+∠2=180°,∴a∥b(同旁内角互补,两直线平行),∵∠6=130°,∴∠5=50°,又∵∠4=50°,∴∠4=∠5,∴b∥c(同错角相等,两直线平行),同理可证:d∥e,a∥c
?
?二 与平行线的性质有关的计算和证明
教材母题?(教材P14作业题第2题)
如图,D,E分别是AB,AC上的点.已知∠AED=60°,∠C=60°,∠ADE=40°.
(1)DE与BC平行吗?请说明理由;
(2)求∠B的度数.
解:(1)DE∥BC,理由略 (2)∠B=40°
?
?
?【思想方法】平行线的性质可用“由线定角”这四个字来概括,即通过某两条直线平行来说明某些角相等(或互补).
专题一 与平行线的判定和性质有关的计算与证明
变形1 如图5,两平行直线a,b被直线l所截,且∠1=60°,则∠2的度数为( )
A.30° B.45°
C.60° D.120°
变形2 如图6,AB∥CD,∠C=52°,∠CEA=38°,则∠EAB的度数为( )
A.28° B.45°C.60° D.90°
变形3 如图7,已知AB∥CD,∠DFE=135°,则∠ABE的度数为( )
A.30° B.45°
C.60° D.90°
变形4 如图8,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=( )
A.60° B.120°C.150° D.180°
专题一 与平行线的判定和性质有关的计算与证明
变形5 (1)如图(a),如果∠B+∠E+∠D=360°,那么AB,CD有怎样的关系?为什么?
解:过点E作EF∥AB①,如图(b),
则∠ABE+∠BEF=180°.(__ )
因为∠ABE+∠BED+∠EDC=360°,( )
所以∠FED+∠EDC=__ _°.(等式的性质)
所以FE∥CD②(__ __)
由①,②得AB∥CD.
(2)如图(c),当∠1,∠2,∠3满足条件__ 时,有AB∥CD.
(3)如图(d),当∠B,∠E,∠F,∠D满足条件____
时,有AB∥CD.
变形6 如图①,已知AC∥BD,点P是直线AC,BD间的一点,连结AB,AP,BP,过点P作直线MN∥AC.
(1)MN与BD的位置关系是什么,请说明理由;
(2)试说明∠APB=∠PBD+∠PAC;
(3)如图②,当点P在直线AC上方时,(2)中的三个角的数量关系是否仍然成立?
如果成立,试说明理由;如果不成立,试探索它们存在的关系,并说明理由.
解:(1)平行,理由:∵AC∥BD,MN∥AC,∴MN∥BD
(2)∵AC∥BD,MN∥BD,
∴∠PBD=∠MPB,∠PAC=∠APM,∴∠APB=∠MPB+∠APM=∠PBD+∠PAC.
(3)不成立,它们之间的关系是∠APB=∠PBD-∠PAD.理由:如图②,过点P作PQ∥AC,
∵AC∥BD,∴PQ∥AC∥BD,∴∠PAC=∠APQ,∠PBD=∠BPQ,∴∠APB=∠BPQ-∠APQ=∠PBD-∠PAC.
?
?
?
?
?
一、选择题(每小题4分,共32分)
1.如图,将三角尺与直尺贴在一起,使三角尺的直角顶点C(∠ACB=90°)在直尺的一边上,若∠1=30°,则∠2的度数等于( )A.75° B.60° C.45° D.30°
2.如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )
A.80° B.100° C.110° D.120°
3.如图,△ABC的三个顶点分别在直线a,b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是( )
A.40° B.60° C.80° D.120°
4.一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是( )
A.75° B.115° C.65° D.105°
5.如图,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能判定a∥b的条件的序号是( )
A.①②
B.①③
C.①④
D.③④
6.一辆汽车在公路上行驶,两次拐弯后,仍在后来的方向上平行行驶,那么两次拐弯的角度可能是( )
A.先向左转130°,再向左转50°
B.先向左转50°,再向右转50°
C.先向左转50°,再向右转40°
D.先向左转50°,再向左转40°
7.如图所示,过点P画∠1=∠2,使直线a平行于直线b的依据是( )
A.两直线平行,同位角相等
B.同位角相等,两直线平行
C.两直线平行,内错角相等
D.内错角相等,两直线平行
8.如图所示,已知直线BF,CD相交于点O,∠D=60°,下面判定两条直线平行正确的是( )
A.当∠C=60°时,AB∥CD
B.当∠A=60°时,AC∥DE
C.当∠E=140°时,CD∥EF
D.当∠BOC=120°时,BF∥DE
9.如图,一个零件ABCD需要AB边与CD边平行,现只有一个
量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零
件合格吗?__ __(填“合格”或“不合格”).
10.如图,请填写一个适当的条件:使得DE∥AB
__答案不唯一,如∠ABD=∠D或∠ABE=∠DEC
或∠ABE+∠DEB=180°__,.
11.如图所示,BE是AB的延长线,由 可以判断∠CBE=∠C,根据是
两直线平行,内错角相__.
12.如图,线段CD是由线段AB向左平移____格,
再向下平移____格后得到的.
13.(8分)看图填空:
(1)∵∠BCD=∠ABC(已知),
∴__AB__∥__CD__(内错角相等,两直线平行);
(2)∵∠DBE=∠CAB(已知),
∴__AC__∥__BD__(同位角相等,两直线平行);
(3)∵∠ADF+__∠F__=180°(已知),
∴AD∥BF(__同旁内角互补,两直线平行__).
14.(10分)如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
解:a∥c,理由:∵∠1=∠2,∴a∥b(内错角相等,两直线平行),∵∠3+∠4=180°,∴b∥c(同旁内角互补,两直线平行),∴a∥c
?
?
?
?
15.(10分)如图,DB∥FG∥EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD的度数.
解:∵FG∥EC,∠ACE=36°,∴∠ACE=∠CAG=36°(两直线平行,内错角相等),∵AP平分∠BAC,∠PAG=12°,∴∠BAP=∠PAC=∠ACG+∠PAG=36°+12°=48°,∴∠BAG=∠BAP+∠PAG=48°+12°=60°,∵DB∥FG,∴∠ABD=∠BAG=60°(两直线平行,内错角相等)
?
?16.(12分)如图所示,点E在直线 DF上,点B在直线AC上,若∠1=∠2,∠C=∠D,试判断∠A与∠F的关系,并说明理由.
解:∠A=∠F,理由:∵∠1=∠DGF(对顶角相等),∠1=∠2,∴∠DGF=∠2,
∴DB∥EC(同位角相等,两直线平行),∴∠C=∠ABD(两直线平行,同位角相等),
∵∠C=∠D,∴∠ABD=∠D,∴AC∥DF(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等)
?
?
17.(12分)如图,在正方形网格中有一个△ABC,请按下列要求进行操作(只能借助于网格):
(1)请作出△ABC中BC边上的高AE;
(2)作出将△ABC向右平移6格,再向上平移3格后的△DEF;
(3)作一个锐角三角形MNP(要求各顶点在格点上),使其面积等于△ABC的面积.
解:作图略
A.若两条直线不相交,则它们平行
B.若两条直线不平行,则它们相交
C.若两条线段平行,则它们不相交
D.若两条线段不相交,则它们平行
2.(4分)下列表示两条直线平行的方法正确的是( )
A.a∥A B.AB∥cd
C.A∥B D.a∥b
3.(4分)在同一平面内有三条直线,其中只有两条是平行线,那么交点共有( )
A.0个 B.1个
C.2个 D.3个
4.(4分)如图,过点C作线段AB的平行线,下列说法正确的是( )
A.不能作出 B.只能作一条
C.能作两条 D.能作无数条
5.(4分)下列说法不正确的是( )
A.过任意一点P可作已知直线l的一条平行线
B.同一平面内的两条不重合不相交的直线是平行线
C.过直线外一点只能画一条直线与已知直线平行
D.平行于同一条直线的两条直线平行
第1章 平行线 1.1 平行线 6.(4分)把下图中互相平行的线段一一写出来:
GH∥MN,EF∥AB,CD∥PQ__.
7.(6分)在同一平面内,直线l1与l2满足下列条件:
(1)l1与l2没有公共点,则l1与l2__ __;
(2)l1与l2有且只有一个公共点,则l1与l2__ __;
(3)l1与l2有两个公共点,则l1与l2__ __.
8.(4分)如图所示的长方体,用符号表示下列棱的位置关系:A1B1____AB,AA1____BB1, A1D1____C1D1,AD____BC.
第1章 平行线 1.1 平行线
9.(6分)如图所示,点P在∠O的一边OA上,点Q在∠O的另一边OB上,按下列要求画图:
(1)作过点P,Q的直线;
(2)过点P作平行于OB的直线;
(3)过点Q作平行于OA的直线.
解:略
??
?
10.(10分)如图,根据要求画图并填空.
(1)过点A作AE∥BC,交_ __于点E;
(2)过点B作BF∥AD,交_ __于点F;
(3)过点C作CG∥AD,交AB的 __ 于点G;
(4)过点D作DH∥BC,交BA的 __于点H.
解:画图略
??
?
11.(4分)下列说法中,正确的有( )
①若a与c相交,b与c相交,则a与b相交;
②在同一平面内,两直线的位置关系只有两种;
③过一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂直三种.
A.3个 B.2个
C.1个 D.0个
第1章 平行线 1.1 平行线 12.(10分)如图所示,在∠AOB内有一点P.
(1)过点P作l1∥OA;
(2)过点P作l2∥OB;
(3)用量角器量一量l1与l2的夹角与∠O的大小
有怎样的关系?
解:(1)(2)如图所示
(3)l1与l2的夹角有两个:∠1,∠2;
∠1=∠O,∠2+∠O=180°,
所以l1和l2的夹角与∠O相等或互补.
?
13.(10分)如图,点P是∠ABC内一点.
(1)过点P画一条直线平行于直线AB,且与BC交于点D;
(2)过点P画一条直线垂直于直线BC,垂足为点E;
(3)过点P作直线AB的垂线段PF.
解:如图所示:
?
?
第1章 平行线 1.1 平行线 14.(10分)如图所示,在写艺术字时,常常运用画“平行线段”这种基本作图方法,此图是在书写字母“M”.
(1)请从正面,上面,右侧三个不同方向上各找出一组平行线段,并用字母表示出来;
(2)EF与A′B′有何位置关系,CC′与DH有何位置关系?
解:(1)答案不唯一,如正面:C′⊥DHAB∥EF;上面:A′B′∥AB;右侧DD′∥HR
(2)EF∥A′B′,C
?
?
?
?
?
?
?
【综合运用】
15.(16分)如图所示,点D,E是线段AC的三等分点.
(1)过点D作DF∥BC交AB于点F,过点E作EG∥BC交AB于点G;
(2)量出AF,FG,GB的长度(精确到0.1 cm),你有什么发现?
(3)量出FD,GE,BC的长度(精确到0.1 cm),你有什么发现?
(4)根据(3)中发现的规律,若FD=1.5 cm,则EG=__3__ cm,BC=__4.5__ cm.
解:(1)略 (2)量线段长度略,AF=FG=GB
(3)量线段长度略,FD∶GE∶BC=1∶2∶3或FD+BC=2GE (4)3 4.5
?
1.3 平行线的判定 第1课时 平行线的判定(一) 1.(4分)下列说法中正确的是( )
A.两条不相交的直线叫平行线
B.一条直线的平行线有且只有一条
C.同位角相等,两直线平行
D.若两条直线不相交,则它们平行
2.(4分)如图所示,∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
3.(4分)已知同一平面内有三条直线l1,l2,l3,如果l1⊥l2,l2⊥l3,则l1与l3的位置关系是( )
A.平行 B.相交
C.垂直 D.以上都不对
4.(4分)如图所示,直线l1和l2被直线l所截,下列说法中正确的是( )
A.因为∠1和∠2互补,所以l1∥l2
B.当∠2=∠3时,l1∥l2
C.当∠1=∠2时,l1∥l2
D.如果∠1=∠3,那么l1∥l2
5.(4分)如图所示,由∠2=∠1,可以得出的结论是( )
A.AD∥CEB.AD∥BC
C.FG∥CED.FG∥BC
1.3 平行线的判定 第1课时 平行线的判定(一) 6.(4分)如图,两直线a,b被第三条直线c所截,若∠1=50°,∠2=130°,则直线a,b的位置关系是__平行__.
7.(4分)如图所示,要使直线a∥b,已知∠1=60°,则∠2的度数是 _.
8.(4分)如图所示,为了加固房屋,要在屋架上加一根横梁DE,使DE∥BC,如果∠ABC=31°,则∠ADE应为__.
9.(8分)如图,直线AB,CD被直线EF所截,H为CD与EF的交点,GH⊥CD于点H,∠2=30°,∠1=60°.直线AB,CD平行吗?请你说明理由.
解:解:AB∥CD 理由:∵GH⊥CD,∴∠2+∠CHF=90°,
∵∠2=30°,∴∠CHF=60°,∴∠CHF=∠DHE=60°(对顶角),
∠1=60°,∴∠1=∠DHE.∴AB∥CD
?
?
10.(10分)如图,如果∠1=47°,∠2=133°,∠D=47°,
那么BC与DE平行吗?AB与CD呢?请说明理由.
解:BC∥DE,AB∥CD 理由:∵∠2=133°,∠D=47°,
∴∠3=∠D ∴BC∥DE,∴∠1=47°,∠2=133°,∴∠ABC=∠3 ∴AB∥CD
1.3 平行线的判定 第1课时 平行线的判定(一) 11.(4分)如图,下列条件能判定AB∥CE的是( )
A.∠A=∠ECD B.∠B=∠ECD
C.∠B=∠ACE D.∠B=∠ACB
12.(6分)已知某品牌遮阳伞如图①所示,
图②是其剖面图,若AG同时平分∠BAC与∠EDF,且∠BAC=∠EDF,请在下面的括号内填写AC∥DF的理由.
解:∵AG同时平分∠BAC与∠EDF(____),
∴∠DAC=∠BAC,∠GDF=∠EDF
(角平分线的定义__).
又∵∠BAC=∠EDF(__ ,
∴∠DAC=∠GDF(__ __),
∴AC∥DF(__ __).
13.(10分)如图,∠ABC=∠DEC,BP平分∠ABC,EF平分∠DEC,试找出图中的各组平行线,并说明理由.
解:AB∥DE,BP∥EF,∵∠ABC=∠DEC,∴AB∥DE
(同位角相等,两直线平行),∵BP平分∠ABC,
EF平分∠DEC,∴∠PBC=∠FEC,∴BP∥EF
(同位角相等,两直线平行)
?
1.3 平行线的判定 第1课时 平行线的判定(一) 14.(10分)如图所示,EF⊥BC于点F,DE⊥AB于点E,∠B=∠ADE,那么AD,EF平行吗?请说明理由.
解:AD与EF平行,理由:∵EF⊥BC,∴∠EFB=90°,∠B+∠BEF=90°,∵DE⊥AB,
∴∠AED=90°,∠ADE+∠DAE=90°,∵∠B=∠ADE,∴∠BEF=∠DAE,∴AD∥EF(同位角相等,两直线平行)
?
15.(8分)如图,已知∠C=108°,若增加一个条件,使得AB∥CD,试写出所有符合要求的条件.
解:∠FEB=108°或∠AEF=72°或∠AEC=108°或∠BEC=72°
???
【综合运用】
16.(12分)(1)如图①所示,AB,CD,EF是三条公路,且AB⊥EF,CD⊥EF.判断AB与CD的位置关系,并说明理由.
(2)如图②所示,在(1)的条件下,若小路OM平分∠EOB,通往加油站N的岔道O′N平分∠CO′F,试判断OM与O′N的位置关系.
解:(1)∵AB⊥EF,CD⊥EF,∴AB∥CD(同一平面内,垂直于同一直线的两条直线互相平行)
(2)延长NO′至P,∵OM平分∠EOB,O′N平分∠CO′F,∴∠EOM=∠FO′N=45°,
∵∠FO′N=∠EO′P,∴∠EOM=∠EO′P=45°,
∴OM∥O′N(同位角相等,两直线平行)
1.4 平行线的性质 第1课时 平行线的性质(一) 1.(4分)如图,直线a∥b,AC⊥AB,AC交直线b于点C,∠1=60°,则∠2的度数( )
A.50° B.45° C.35° D.30°
2.(4分)如图,已知直线a,b被直线c所截,a∥b,∠1=60°,则∠2的度数为( )
A.30° B.60° C.120° D.150°
3.(4分)如图,AC∥DF,AB∥EF,点D,E分别在AB,AC上,若∠2=50°,则∠1的大小是( )
A.30° B.40° C.50° D.60°
4.(4分)如图所示,AB∥CD,直线AF分别交AB,CD于点A,C,CE平分∠DCF,∠1=100°,则∠2的度数为( )
A.40° B.50° C.60° D.70°
5.(4分)两条平行线被第三条直线所截,则一对同位角的角平分线( )
A.相交 B.平行 C.垂直 D.不能确定
1.4 平行线的性质 第1课时 平行线的性质(一)
6.(4分)已知直线a∥b,若∠1=40°50′,则∠2=__.
7.(4分)如图,直尺一边AB与量角器的零刻度线CD平行,若量角器的一条刻度线OF的读数为70°,OF与AB交于点E,那么∠AEF=____度.
8.(6分)如图所示,已知AB∥DE,EF∥BC,∠B=45°,求∠E的度数.
解:∵AB∥DE(已知),
∴∠B=∠COE(__ __).
∵EF∥BC(已知),
∴∠BOD=∠E(__.
又∵∠BOD=∠COE(__,
∴∠E=∠B=45°(等量代换).
9.(6分)完成下列推理:
如图所示,已知∠1=36°,∠C=74°,∠B=36°,求∠2的度数.
解:因为∠1=__ =36°,所以__ __(同位角相等,两直线平行).
所以∠2=__ 两直线平行,同位角相等).
10.(10分)如图所示,已知∠1=∠2,∠3=90°,求∠4的度数.
解:∵∠1=∠2,∴a∥b(同位角相等,两直线平行),∴∠3=∠4(
两直线平行,同位角相等),∵∠3=90°,∴∠4=90°
?
?
?
?
1.4 平行线的性质 第1课时 平行线的性质(一)
11.(4分)如图所示,∠AOB的两边OA,OB均为平面反光镜,∠AOB=35°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行,则∠DEB的度数是( )
A.35° B.70° C.110° D.120°
12.(4分)如图所示,直线a,b被直线c所截,构成8个角,若a∥b,则这8个角中与∠1相等的角共有___个(不含∠1).
13.(10分)如图所示,已知点D,E,F,分别在AB,AC,BC上,DE∥BC,EF∥AB,则∠1=∠2吗?为什么?
解:∠1=∠2,理由:∵DE∥BC,∴∠1=∠B(两直线平行,同位角相等),∵EF∥AB,∴∠B=∠2(两直线平行,同位角相等),∴∠1=∠2
?
?
14.(10分)如图所示,直线a∥b,∠1=54°,那么∠2,∠3,∠4各是多少度?
解:∠2=54°,∠3=126°,∠4=54°
?
?
?
?
?
?
?
1.4 平行线的性质 第1课时 平行线的性质(一)
15.(10分)如图,EF⊥AB,EF⊥CD,直线GH与AB,CD相交,试说明∠1+∠2=180°.
解:∵EF⊥AB,EF⊥CD,∴AB∥CD(同一平面内,垂直于同一条直线的两条直线互相平行),∵AB∥CD,∴∠1=∠5(两直线平行,同位角相等),∵∠5+∠2=180°,∴∠1+∠2=180°
?
?
?
?
?
?
【综合运用】
16.(12分)如图所示,水渠的两岸互相平行,修渠时要求拐弯处∠1=110°,那么∠2应等于多少度?为什么?
解:∠2=110°,理由:连接BE并延长至G点,∵AB∥DE,∴∠ABE=∠DEG(两直线平行,同位角相等).∵EF∥BC,∴∠CBE=∠FEG(两直线平行,同位角相等),∵∠1=∠ABE+∠CBE=110°,∴∠2=∠DEG+∠FEG=110°
?
专题一 与平行线的判定和性质有关的计算与证明
一 与平行线的判定有关的计算和证明
教材母题?(教材P11作业题第3题)
如图,已知直线l1,l2被直线AB所截,AC⊥l2于点C.若∠1=50°,∠2=40°,则l1与l2平行吗?请说明理由.
解:l1∥l2,理由:∵∠1=50°,∠2=40°,∴∠1+∠2=90°,
∴AC⊥l1,又∵AC⊥l2,∴l1∥l2
?
?【思想方法】 平行线的判定可用“由角定线”这四个字来概括,即通过说明
某些角相等(或互补)来判定两直线平行.
变形1 如图1,已知直线a,b,c,d,其中c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2等于( )
A.60° B.50° C.40° D.30°
变形2 如图2,若∠1=40°,∠2=40°,∠3=116°30′,则∠4=__.
变形3 如图3,∠1+∠2=180°,∠3=100°,则∠4等于( )
A.70° B.80° C.90° D.100°
变形4 如图4,∠1=∠2,∠3=40°,则∠4等于( )
A.120° B.130° C.140° D.40°
专题一 与平行线的判定和性质有关的计算与证明
变形5 如图,已知∠1的度数是它的补角的3倍,∠2=45°,那么AB∥CD吗?为什么?
解:AB∥CD,理由:∵∠1的度数是它的补角的3倍,∴∠1=135°,∴∠MNC=45°,∴∠2=∠MNC,∴AB∥CD(同位角相等,两直线平行)
?
?
?
变形6 如图所示,已知∠1=50°,∠2=130°,∠4=50°,∠6=130°,试说明a∥b,b∥c,d∥e,a∥c.
证明:∵∠1=50°,∠2=130°,∠1+∠2=180°,∴a∥b(同旁内角互补,两直线平行),∵∠6=130°,∴∠5=50°,又∵∠4=50°,∴∠4=∠5,∴b∥c(同错角相等,两直线平行),同理可证:d∥e,a∥c
?
?二 与平行线的性质有关的计算和证明
教材母题?(教材P14作业题第2题)
如图,D,E分别是AB,AC上的点.已知∠AED=60°,∠C=60°,∠ADE=40°.
(1)DE与BC平行吗?请说明理由;
(2)求∠B的度数.
解:(1)DE∥BC,理由略 (2)∠B=40°
?
?
?【思想方法】平行线的性质可用“由线定角”这四个字来概括,即通过某两条直线平行来说明某些角相等(或互补).
专题一 与平行线的判定和性质有关的计算与证明
变形1 如图5,两平行直线a,b被直线l所截,且∠1=60°,则∠2的度数为( )
A.30° B.45°
C.60° D.120°
变形2 如图6,AB∥CD,∠C=52°,∠CEA=38°,则∠EAB的度数为( )
A.28° B.45°C.60° D.90°
变形3 如图7,已知AB∥CD,∠DFE=135°,则∠ABE的度数为( )
A.30° B.45°
C.60° D.90°
变形4 如图8,AB∥CD∥EF,AC∥DF,若∠BAC=120°,则∠CDF=( )
A.60° B.120°C.150° D.180°
专题一 与平行线的判定和性质有关的计算与证明
变形5 (1)如图(a),如果∠B+∠E+∠D=360°,那么AB,CD有怎样的关系?为什么?
解:过点E作EF∥AB①,如图(b),
则∠ABE+∠BEF=180°.(__ )
因为∠ABE+∠BED+∠EDC=360°,( )
所以∠FED+∠EDC=__ _°.(等式的性质)
所以FE∥CD②(__ __)
由①,②得AB∥CD.
(2)如图(c),当∠1,∠2,∠3满足条件__ 时,有AB∥CD.
(3)如图(d),当∠B,∠E,∠F,∠D满足条件____
时,有AB∥CD.
变形6 如图①,已知AC∥BD,点P是直线AC,BD间的一点,连结AB,AP,BP,过点P作直线MN∥AC.
(1)MN与BD的位置关系是什么,请说明理由;
(2)试说明∠APB=∠PBD+∠PAC;
(3)如图②,当点P在直线AC上方时,(2)中的三个角的数量关系是否仍然成立?
如果成立,试说明理由;如果不成立,试探索它们存在的关系,并说明理由.
解:(1)平行,理由:∵AC∥BD,MN∥AC,∴MN∥BD
(2)∵AC∥BD,MN∥BD,
∴∠PBD=∠MPB,∠PAC=∠APM,∴∠APB=∠MPB+∠APM=∠PBD+∠PAC.
(3)不成立,它们之间的关系是∠APB=∠PBD-∠PAD.理由:如图②,过点P作PQ∥AC,
∵AC∥BD,∴PQ∥AC∥BD,∴∠PAC=∠APQ,∠PBD=∠BPQ,∴∠APB=∠BPQ-∠APQ=∠PBD-∠PAC.
?
?
?
?
?
一、选择题(每小题4分,共32分)
1.如图,将三角尺与直尺贴在一起,使三角尺的直角顶点C(∠ACB=90°)在直尺的一边上,若∠1=30°,则∠2的度数等于( )A.75° B.60° C.45° D.30°
2.如图,梯子的各条横档互相平行,若∠1=80°,则∠2的度数是( )
A.80° B.100° C.110° D.120°
3.如图,△ABC的三个顶点分别在直线a,b上,且a∥b,若∠1=120°,∠2=80°,则∠3的度数是( )
A.40° B.60° C.80° D.120°
4.一只因损坏而倾斜的椅子,从背后看到的形状如图,其中两组对边的平行关系没有发生变化,若∠1=75°,则∠2的大小是( )
A.75° B.115° C.65° D.105°
5.如图,直线a,b被直线c所截,现给出下列四个条件:①∠1=∠5;②∠1=∠7;③∠2+∠3=180°;④∠4=∠7.其中能判定a∥b的条件的序号是( )
A.①②
B.①③
C.①④
D.③④
6.一辆汽车在公路上行驶,两次拐弯后,仍在后来的方向上平行行驶,那么两次拐弯的角度可能是( )
A.先向左转130°,再向左转50°
B.先向左转50°,再向右转50°
C.先向左转50°,再向右转40°
D.先向左转50°,再向左转40°
7.如图所示,过点P画∠1=∠2,使直线a平行于直线b的依据是( )
A.两直线平行,同位角相等
B.同位角相等,两直线平行
C.两直线平行,内错角相等
D.内错角相等,两直线平行
8.如图所示,已知直线BF,CD相交于点O,∠D=60°,下面判定两条直线平行正确的是( )
A.当∠C=60°时,AB∥CD
B.当∠A=60°时,AC∥DE
C.当∠E=140°时,CD∥EF
D.当∠BOC=120°时,BF∥DE
9.如图,一个零件ABCD需要AB边与CD边平行,现只有一个
量角器,测得拐角∠ABC=120°,∠BCD=60°,这个零
件合格吗?__ __(填“合格”或“不合格”).
10.如图,请填写一个适当的条件:使得DE∥AB
__答案不唯一,如∠ABD=∠D或∠ABE=∠DEC
或∠ABE+∠DEB=180°__,.
11.如图所示,BE是AB的延长线,由 可以判断∠CBE=∠C,根据是
两直线平行,内错角相__.
12.如图,线段CD是由线段AB向左平移____格,
再向下平移____格后得到的.
13.(8分)看图填空:
(1)∵∠BCD=∠ABC(已知),
∴__AB__∥__CD__(内错角相等,两直线平行);
(2)∵∠DBE=∠CAB(已知),
∴__AC__∥__BD__(同位角相等,两直线平行);
(3)∵∠ADF+__∠F__=180°(已知),
∴AD∥BF(__同旁内角互补,两直线平行__).
14.(10分)如图,已知直线a,b,c,d,e,且∠1=∠2,∠3+∠4=180°,则a与c平行吗?为什么?
解:a∥c,理由:∵∠1=∠2,∴a∥b(内错角相等,两直线平行),∵∠3+∠4=180°,∴b∥c(同旁内角互补,两直线平行),∴a∥c
?
?
?
?
15.(10分)如图,DB∥FG∥EC,∠ACE=36°,AP平分∠BAC,∠PAG=12°,求∠ABD的度数.
解:∵FG∥EC,∠ACE=36°,∴∠ACE=∠CAG=36°(两直线平行,内错角相等),∵AP平分∠BAC,∠PAG=12°,∴∠BAP=∠PAC=∠ACG+∠PAG=36°+12°=48°,∴∠BAG=∠BAP+∠PAG=48°+12°=60°,∵DB∥FG,∴∠ABD=∠BAG=60°(两直线平行,内错角相等)
?
?16.(12分)如图所示,点E在直线 DF上,点B在直线AC上,若∠1=∠2,∠C=∠D,试判断∠A与∠F的关系,并说明理由.
解:∠A=∠F,理由:∵∠1=∠DGF(对顶角相等),∠1=∠2,∴∠DGF=∠2,
∴DB∥EC(同位角相等,两直线平行),∴∠C=∠ABD(两直线平行,同位角相等),
∵∠C=∠D,∴∠ABD=∠D,∴AC∥DF(内错角相等,两直线平行),
∴∠A=∠F(两直线平行,内错角相等)
?
?
17.(12分)如图,在正方形网格中有一个△ABC,请按下列要求进行操作(只能借助于网格):
(1)请作出△ABC中BC边上的高AE;
(2)作出将△ABC向右平移6格,再向上平移3格后的△DEF;
(3)作一个锐角三角形MNP(要求各顶点在格点上),使其面积等于△ABC的面积.
解:作图略
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
