【四清导航】2015春七年级数学下册(浙教版,A本)同步习题精讲课件:第2章+二元一次方程组(共31张PPT)
文档属性
| 名称 | 【四清导航】2015春七年级数学下册(浙教版,A本)同步习题精讲课件:第2章+二元一次方程组(共31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-31 11:44:39 | ||
图片预览











文档简介
课件31张PPT。 第2章 二元一次方程组 2.1 二元一次方程
第2章 二元一次方程组 2.1 二元一次方程
第2章 二元一次方程组 2.1 二元一次方程
第2章 二元一次方程组 2.1 二元一次方程
第2章 二元一次方程组 2.1 二元一次方程 17.(9分)某长方形长为y cm,宽为x cm,若宽的3倍比长多2 cm,求:
(1)x,y满足的关系式; (2)当x=2时,y的值;
(3)当y=10时,x的值.
解:(1)3x-y=2 (2)当x=2时,y=4 (3)当y=10时,x=4
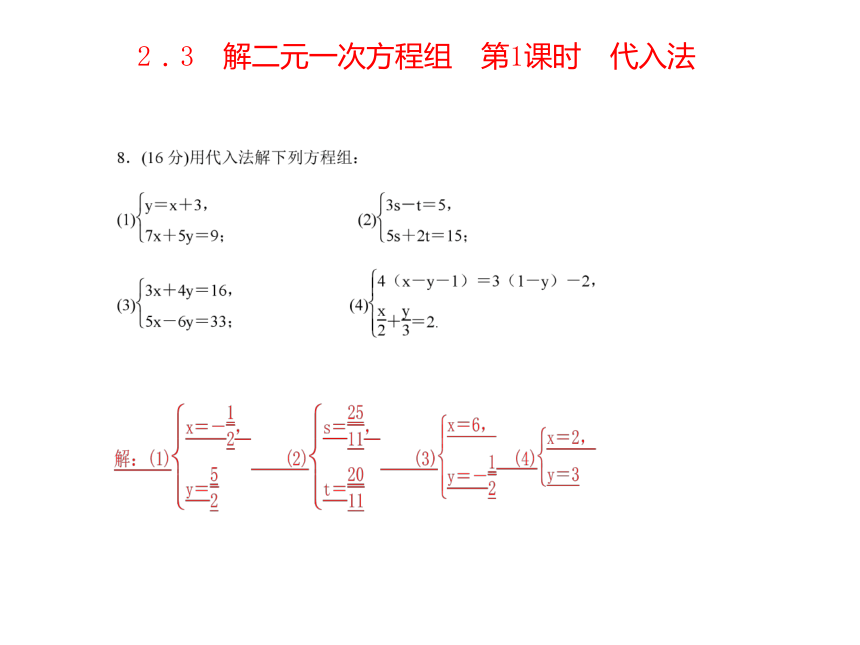
2.3 解二元一次方程组 第1课时 代入法
2.3 解二元一次方程组 第1课时 代入法
2.3 解二元一次方程组 第1课时 代入法
2.3 解二元一次方程组 第1课时 代入法
2.3 解二元一次方程组 第1课时 代入法
2.3 解二元一次方程组 第1课时 代入法
第2课时 应用二元一次方程组解决较复杂的实际问题 1.(5分)端午节时,王老师用72元钱买了荷包和五彩绳共20个.其中荷包每个4元,五彩绳每个3元,设王老师购买荷包x个,五彩绳y个,根据题意,下列列出的方程组正确的是( )
2.(5分)如图所示,射线OC的端点O在直线AB上,∠1的度数是x°,比∠2的度数y°的2倍多10°,则下列方程组正确的为( )
第2课时 应用二元一次方程组解决较复杂的实际问题 3.(5分)用彩色和单色的两种地砖铺地,彩色地砖14元/块,单色地砖12元/块,若买单色地砖的数量比彩色地砖的数量的2倍少15块,买两种地砖共用了1340元,设购买彩色地砖x块,单色地砖y块,则根据题意可列方程组____.
4.(5分)某校有150名学生参加数学智力竞赛.经统计,这些学生的平均分为60分,其中及格学生的平均分为70分,不及格学生的平均分为50分,则这些学生中,及格的有____人,不及格的有____人.
5.(10分)用甲、乙两种原料配制某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表所示:
现要求用72元钱配制含5 000单位的维生素C的这种饮料,问:应分别购买这两种原料各多少千克?
第2课时 应用二元一次方程组解决较复杂的实际问题
6.(10分)某城市规定:出租车起步价允许行驶的最远路程为3千米,超过3千米的部分按每千米另外收费.甲说:“我乘这种出租车走了11千米,付了17元”;乙说:“我乘这种出租车走了23千米,付了35元”.请你算一算这种出租车的起步价是多少元,以及超过3千米后,每千米的车费是多少元.
?
7.(10分)在水果店里,小李买了5 kg苹果,3 kg梨,老板少要了2元,收了50元;老王买了11 kg苹果,5 kg梨,老板按九折收钱,收了90元.该店的苹果和梨的单价各是多少元?
8.(5分)公式s=s0+vt表示的是路程s与时间t之间的关系(其中s0,v都是不等于零的常数),当t=5时,s=260;当t=7时,s=340,则s0,v的值分别是( )
A.s0=60,v=40 B.s0=-60,v=40
C.s0=60,v=-40 D.s0=-60,v=-40
9.(5分)甲种电影票每张20元,乙种电影票每张15元,若购买甲、乙两种电影票共40张,恰好用去700元,则甲种电影票买了____张.
第2课时 应用二元一次方程组解决较复杂的实际问题
10.(10分)老师布置了一个探究活动作业:仅用一架天平和一个10克的砝码测量壹元硬币和伍角硬币的质量(注:同种类的每枚硬币质量相同).聪明的孔明同学找来足够多的壹元和伍角的硬币,经过探究得到以下两个探究记录:
请你用所学的数学知识计算出一枚壹元硬币多少克,一枚伍角硬币多少克?
11.(12分)某学校组织学生乘汽车去自然保护区野营,先以60 km/h的速度走平路,后又以30 km/h的速度爬坡,共用了6.5 h;原路返回时,汽车以40 km/h的速度下坡,又以50 km/h的速度走平路,共用了6 h.问平路和坡路各有多远?
?
第2课时 应用二元一次方程组解决较复杂的实际问题 12.(18分)已知用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
2.5 三元一次方程组及其解法(选学)
2.5 三元一次方程组及其解法(选学) 5.(4分)为了奖励进步较大的学生,某班决定购买甲、乙、丙三种笔记本作为奖品,其单价分别为4元、5元、6元,购买这些笔记本需要花60元;经过协商,每种笔记本单价下降1元,结果只花了48元,那么甲种笔记本可能购买了( )
A.11本 B.9本 C.7本 D.4本
2.5 三元一次方程组及其解法(选学)
2.5 三元一次方程组及其解法(选学) 16.(8分)对于有理数x,y,定义新运算x*y=ax+by+c,其中a,b,c是常数,等式右边是通常的加法与乘法运算,已知1*2=9,(-3)*3=6,0*1=2,求(-2)*5的值.
17.(8分)一个三位数,如果把它的个位数与百位数字交换位置,那么所得的新数比原数小99,且各位数字之和为14,十位数字是个位数字与百位数字之和.求这个三位数
.
2.5 三元一次方程组及其解法(选学) 18.(10分)为了组织一个50人的旅游团开展“乡间民俗”游,旅游团计划住村民家,已知住宿客房有三人间、两人间、单人间三种,收费标准是三人间每人每晚20元,两人间每人每晚30元,单人间每人每晚50元,共住20间客房,每间客房都住满,问旅游团如何安排住宿才能够使住宿费最低,并说明理由.
检测内容:第2章
检测内容:第2章
检测内容:第2章14.我国古代数学名著《孙子算经》中有这样一题,今有鸡兔同笼,上有35头,下有94足,问鸡兔各几何?此题的答案是鸡有23只,兔有12只,现在小敏将此题改编为今有鸡兔同笼,上有33头,下有88足,问鸡免各几何?则此时的答案是:鸡有____只,兔有____只.
15.老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为____元.
检测内容:第2章18.(10分)编钟旅行社组织200人分别到台北和高雄旅游,到高雄的人数比到台北的人数的2倍少1人,求到两地旅游的人数各是多少?
19.(10分)为方便市民出行,减轻城市中心交通压力,某市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线,2号线每千米的平均造价分别是多少亿元?
(2)除1,2号线外,市政府规划到2018年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
检测内容:第2章
第2章 二元一次方程组 2.1 二元一次方程
第2章 二元一次方程组 2.1 二元一次方程
第2章 二元一次方程组 2.1 二元一次方程
第2章 二元一次方程组 2.1 二元一次方程 17.(9分)某长方形长为y cm,宽为x cm,若宽的3倍比长多2 cm,求:
(1)x,y满足的关系式; (2)当x=2时,y的值;
(3)当y=10时,x的值.
解:(1)3x-y=2 (2)当x=2时,y=4 (3)当y=10时,x=4
2.3 解二元一次方程组 第1课时 代入法
2.3 解二元一次方程组 第1课时 代入法
2.3 解二元一次方程组 第1课时 代入法
2.3 解二元一次方程组 第1课时 代入法
2.3 解二元一次方程组 第1课时 代入法
2.3 解二元一次方程组 第1课时 代入法
第2课时 应用二元一次方程组解决较复杂的实际问题 1.(5分)端午节时,王老师用72元钱买了荷包和五彩绳共20个.其中荷包每个4元,五彩绳每个3元,设王老师购买荷包x个,五彩绳y个,根据题意,下列列出的方程组正确的是( )
2.(5分)如图所示,射线OC的端点O在直线AB上,∠1的度数是x°,比∠2的度数y°的2倍多10°,则下列方程组正确的为( )
第2课时 应用二元一次方程组解决较复杂的实际问题 3.(5分)用彩色和单色的两种地砖铺地,彩色地砖14元/块,单色地砖12元/块,若买单色地砖的数量比彩色地砖的数量的2倍少15块,买两种地砖共用了1340元,设购买彩色地砖x块,单色地砖y块,则根据题意可列方程组____.
4.(5分)某校有150名学生参加数学智力竞赛.经统计,这些学生的平均分为60分,其中及格学生的平均分为70分,不及格学生的平均分为50分,则这些学生中,及格的有____人,不及格的有____人.
5.(10分)用甲、乙两种原料配制某种饮料,已知这两种原料的维生素C含量及购买这两种原料的价格如下表所示:
现要求用72元钱配制含5 000单位的维生素C的这种饮料,问:应分别购买这两种原料各多少千克?
第2课时 应用二元一次方程组解决较复杂的实际问题
6.(10分)某城市规定:出租车起步价允许行驶的最远路程为3千米,超过3千米的部分按每千米另外收费.甲说:“我乘这种出租车走了11千米,付了17元”;乙说:“我乘这种出租车走了23千米,付了35元”.请你算一算这种出租车的起步价是多少元,以及超过3千米后,每千米的车费是多少元.
?
7.(10分)在水果店里,小李买了5 kg苹果,3 kg梨,老板少要了2元,收了50元;老王买了11 kg苹果,5 kg梨,老板按九折收钱,收了90元.该店的苹果和梨的单价各是多少元?
8.(5分)公式s=s0+vt表示的是路程s与时间t之间的关系(其中s0,v都是不等于零的常数),当t=5时,s=260;当t=7时,s=340,则s0,v的值分别是( )
A.s0=60,v=40 B.s0=-60,v=40
C.s0=60,v=-40 D.s0=-60,v=-40
9.(5分)甲种电影票每张20元,乙种电影票每张15元,若购买甲、乙两种电影票共40张,恰好用去700元,则甲种电影票买了____张.
第2课时 应用二元一次方程组解决较复杂的实际问题
10.(10分)老师布置了一个探究活动作业:仅用一架天平和一个10克的砝码测量壹元硬币和伍角硬币的质量(注:同种类的每枚硬币质量相同).聪明的孔明同学找来足够多的壹元和伍角的硬币,经过探究得到以下两个探究记录:
请你用所学的数学知识计算出一枚壹元硬币多少克,一枚伍角硬币多少克?
11.(12分)某学校组织学生乘汽车去自然保护区野营,先以60 km/h的速度走平路,后又以30 km/h的速度爬坡,共用了6.5 h;原路返回时,汽车以40 km/h的速度下坡,又以50 km/h的速度走平路,共用了6 h.问平路和坡路各有多远?
?
第2课时 应用二元一次方程组解决较复杂的实际问题 12.(18分)已知用2辆A型车和1辆B型车装满货物一次可运货10吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都装满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
2.5 三元一次方程组及其解法(选学)
2.5 三元一次方程组及其解法(选学) 5.(4分)为了奖励进步较大的学生,某班决定购买甲、乙、丙三种笔记本作为奖品,其单价分别为4元、5元、6元,购买这些笔记本需要花60元;经过协商,每种笔记本单价下降1元,结果只花了48元,那么甲种笔记本可能购买了( )
A.11本 B.9本 C.7本 D.4本
2.5 三元一次方程组及其解法(选学)
2.5 三元一次方程组及其解法(选学) 16.(8分)对于有理数x,y,定义新运算x*y=ax+by+c,其中a,b,c是常数,等式右边是通常的加法与乘法运算,已知1*2=9,(-3)*3=6,0*1=2,求(-2)*5的值.
17.(8分)一个三位数,如果把它的个位数与百位数字交换位置,那么所得的新数比原数小99,且各位数字之和为14,十位数字是个位数字与百位数字之和.求这个三位数
.
2.5 三元一次方程组及其解法(选学) 18.(10分)为了组织一个50人的旅游团开展“乡间民俗”游,旅游团计划住村民家,已知住宿客房有三人间、两人间、单人间三种,收费标准是三人间每人每晚20元,两人间每人每晚30元,单人间每人每晚50元,共住20间客房,每间客房都住满,问旅游团如何安排住宿才能够使住宿费最低,并说明理由.
检测内容:第2章
检测内容:第2章
检测内容:第2章14.我国古代数学名著《孙子算经》中有这样一题,今有鸡兔同笼,上有35头,下有94足,问鸡兔各几何?此题的答案是鸡有23只,兔有12只,现在小敏将此题改编为今有鸡兔同笼,上有33头,下有88足,问鸡免各几何?则此时的答案是:鸡有____只,兔有____只.
15.老师打算购买气球装扮学校“六一”儿童节活动会场,气球的种类有笑脸和爱心两种,两种气球的价格不同,但同一种气球的价格相同,由于会场布置需要,购买时以一束(4个气球)为单位,已知第一、二束气球的价格如图所示,则第三束气球的价格为____元.
检测内容:第2章18.(10分)编钟旅行社组织200人分别到台北和高雄旅游,到高雄的人数比到台北的人数的2倍少1人,求到两地旅游的人数各是多少?
19.(10分)为方便市民出行,减轻城市中心交通压力,某市正在修建贯穿星城南北、东西的地铁1、2号线.已知修建地铁1号线24千米和2号线22千米共需投资265亿元;若1号线每千米的平均造价比2号线每千米的平均造价多0.5亿元.
(1)求1号线,2号线每千米的平均造价分别是多少亿元?
(2)除1,2号线外,市政府规划到2018年还要再建91.8千米的地铁线网.据预算,这91.8千米地铁线网每千米的平均造价是1号线每千米的平均造价的1.2倍,则还需投资多少亿元?
检测内容:第2章
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
