【四清导航】2015春七年级数学下册(浙教版,B本)同步习题精讲课件:第一章(共24张PPT)
文档属性
| 名称 | 【四清导航】2015春七年级数学下册(浙教版,B本)同步习题精讲课件:第一章(共24张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-12-31 15:10:30 | ||
图片预览





文档简介
课件24张PPT。第1章 平行线
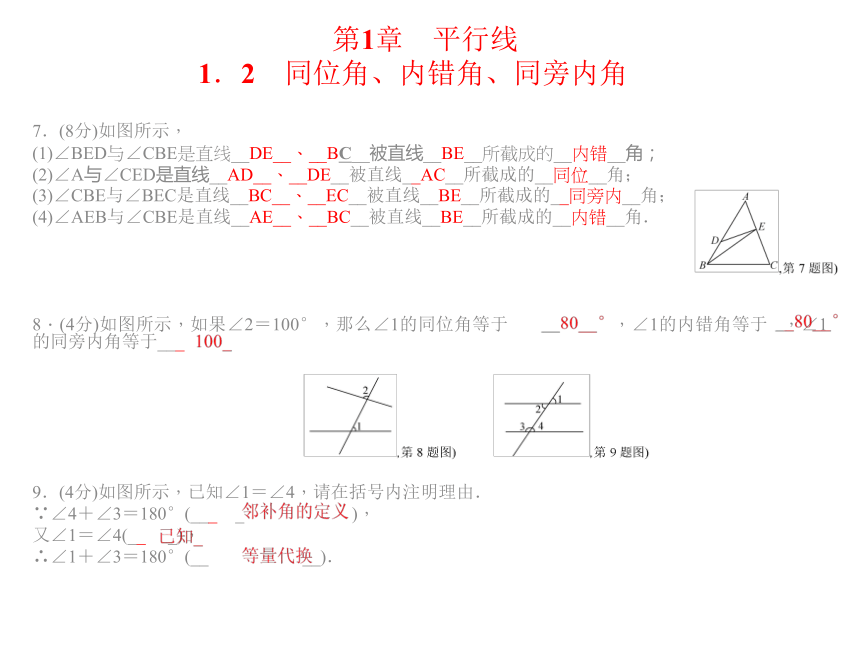
1.2 同位角、内错角、同旁内角1.(4分)如图,与∠1是同位角的是( )
A.∠2 B.∠3
C.∠4 D.∠5
2.(4分)如图, ∠CED和∠BDE是( )
A.同位角 B.内错角
C.同旁内角 D.互为补角
3.(4分)如图,与∠1是内错角的是( )
A.∠2 B.∠3
C.∠4 D.∠5第1章 平行线 1.2 同位角、内错角、同旁内角4.(4分)如图,若直线MN与△ABC的边AB,AC分别交于点E,F,则图中的内错角有( )
A.2对 B.4 C.6对 D.8对
5.(4分)下列图形中,∠1与∠2不是同位角的是( )
6.(4分)如图,∠B的同旁内角是
_∠BCD与∠BAD__.第1章 平行线 1.2 同位角、内错角、同旁内角7.(8分)如图所示,
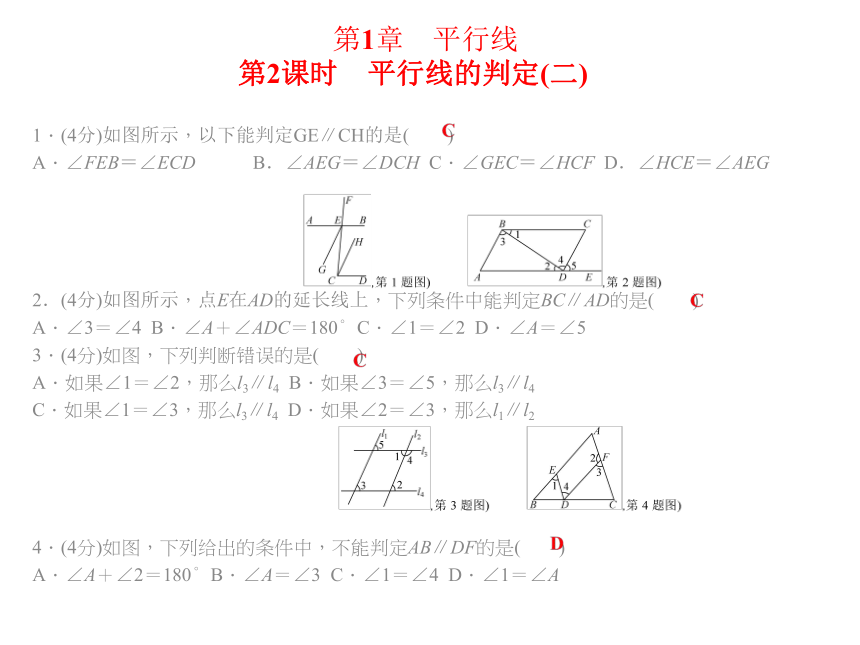
(1)∠BED与∠CBE是直线__DE__、__BC__被直线__BE__所截成的__内错__角;
(2)∠A与∠CED是直线__AD__、__DE__被直线__AC__所截成的__同位__角;
(3)∠CBE与∠BEC是直线__BC__、__EC__被直线__BE__所截成的__同旁内__角;
(4)∠AEB与∠CBE是直线__AE__、__BC__被直线__BE__所截成的__内错__角.
8.(4分)如图所示,如果∠2=100°,那么∠1的同位角等于 ,∠1的内错角等于 ,∠1的同旁内角等于___
9.(4分)如图所示,已知∠1=∠4,请在括号内注明理由.
∵∠4+∠3=180°(___ _ ),
又∠1=∠4(__ _),
∴∠1+∠3=180°(__ __).第1章 平行线 1.2 同位角、内错角、同旁内角9.(4分)如图所示,已知∠1=∠4,请在括号内注明理由.
∵∠4+∠3=180°(__ __),
又∠1=∠4(__ __),
∴∠1+∠3=180°(__ __).
10.(10分)如图,试回答:
(1)∠1与∠2,∠3与∠4分别是具有怎样位置关系的角?
(2)当∠1=∠2时,∠3与∠4是具有怎样大小关系的角?
解:(1)∠1与∠2是同位角,∠3与∠4是同旁内角
(2)∠3与∠4互补
?第1章 平行线 1.2 同位角、内错角、同旁内角11.(6分)如图所示,请从“A.同位角;B.内错角;C.同旁内角;D.对顶角;E.以上都不是”中选出正确答案,并把它的代号填入题后的括号内.
(1)∠1与∠B是( );
(2)∠2与∠B是( );
(3)∠3与∠B是( );
(4)∠C与∠BAE是( );
(5)∠BAF与∠DAG是( );
(6)∠B与∠BAF是( ).
12.(4分)如图所示,直线l是l1与l2的截线.找出∠1的同位角,标上∠2,找出∠1的同旁内角,标上∠3.图中∠2、∠3的标法正确的是( )
13.(4分)如图所示,与∠α构成同位角的角的个数为( )
A.1个 B.2个
C.3个 D.4个14.(4分)如图,有下列6种说法:(1)∠1与∠4是内错角;(2)∠1与∠2是同位角;(3)∠2与∠4是内错角;(4)∠4与∠5是同旁内角;(5)∠2与∠4是同位角;(6)∠2与∠5是内错角.其中正确的有( C )
A.1个 B.2个 C.3个 D.4个第1章 平行线 1.2 同位角、内错角、同旁内角15.(10分)如图,Rt△ABC中,∠C=90°,DE⊥AC,交AB于点D,交AC于点E.
(1)说出当BC,DE被AB所截时,∠3的同位角、内错角和同旁内角.
(2)试说明∠1=∠2=∠3的理由.
解:(1)∠3的同位角是∠1,∠3的内错角是∠2,∠3的同旁内角是∠BDE (2)理由:∵∠C=90°,∴∠A+∠3=90°,∵DE⊥AC,∴∠A+∠1=90°,∴∠1=∠3,又∵∠1=∠2(对顶角),∴∠1=∠2=∠3
?
?
?
16.(12分)如图所示,指出图中∠1和∠A,∠3和∠A,∠2和∠B,∠BCD和∠B,∠3和∠B,∠A和∠B各是什么位置关系的角?并指出各是由哪两条直线被哪一条直线所截形成的角?
解:∠1和∠A是同位角,是由直线CE和AB被直线AD所截形成; ∠3和∠A是同旁内角,是由直线BC和AB被直线AD所截形成; ∠2和∠B是内错角,是由直线CE和AB被直线BC所截形成; ∠BCD和∠B是内错角,是由直线AD和AB被直线BC所截形成;∠3和∠B是同旁内角,是由直线AD和AB被直线BC所截形成; ∠A和∠B是同旁内角,是由直线AD和BC被直线AB所截形成
?
17.(10分)如图所示,在标出的7个角中,与∠1是内错角、同旁内角的各是哪几个?与∠5是同位角的是哪几个?
解:与∠1是内错角的有∠4,∠7;与∠1是同旁内角的有∠5,∠6;与∠5是同位角的有∠7
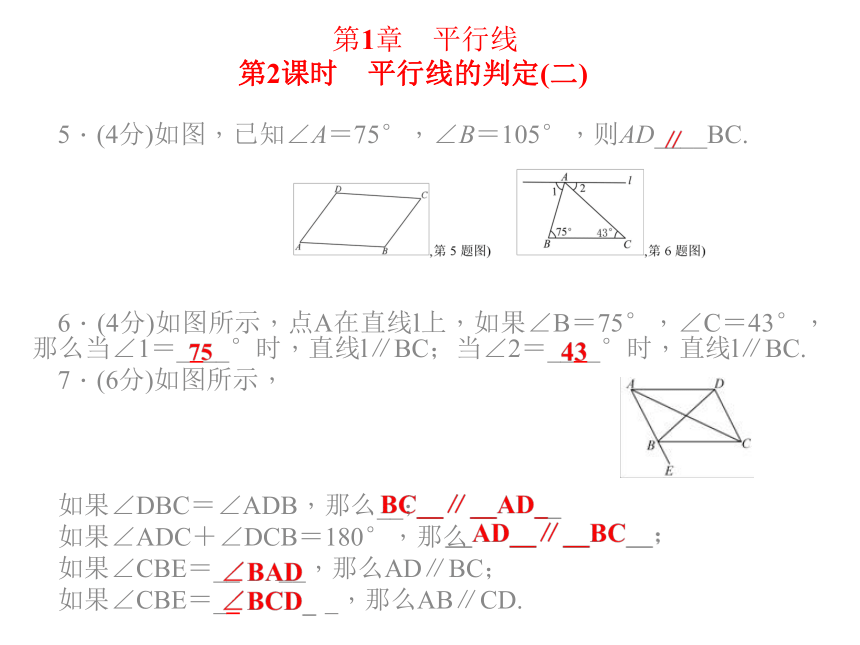
?第1章 平行线 第2课时 平行线的判定(二)1.(4分)如图所示,以下能判定GE∥CH的是( )
A.∠FEB=∠ECD B.∠AEG=∠DCH C.∠GEC=∠HCF D.∠HCE=∠AEG
2.(4分)如图所示,点E在AD的延长线上,下列条件中能判定BC∥AD的是( )
A.∠3=∠4 B.∠A+∠ADC=180° C.∠1=∠2 D.∠A=∠5
3.(4分)如图,下列判断错误的是( )
A.如果∠1=∠2,那么l3∥l4 B.如果∠3=∠5,那么l3∥l4
C.如果∠1=∠3,那么l3∥l4 D.如果∠2=∠3,那么l1∥l2
4.(4分)如图,下列给出的条件中,不能判定AB∥DF的是( )
A.∠A+∠2=180° B.∠A=∠3 C.∠1=∠4 D.∠1=∠A
第1章 平行线 第2课时 平行线的判定(二)5.(4分)如图,已知∠A=75°,∠B=105°,则AD____BC.
?
6.(4分)如图所示,点A在直线l上,如果∠B=75°,∠C=43°,那么当∠1=____°时,直线l∥BC;当∠2=____°时,直线l∥BC.
7.(6分)如图所示,
如果∠DBC=∠ADB,那么__;
如果∠ADC+∠DCB=180°,那么
如果∠CBE=__ __,那么AD∥BC;
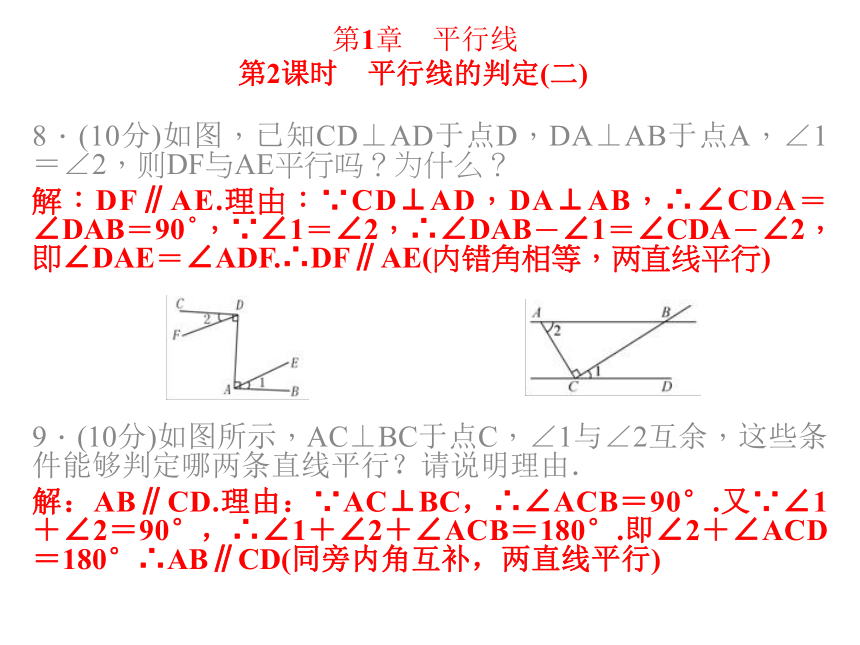
如果∠CBE=__ _,那么AB∥CD.第1章 平行线 第2课时 平行线的判定(二)8.(10分)如图,已知CD⊥AD于点D,DA⊥AB于点A,∠1=∠2,则DF与AE平行吗?为什么?
解:DF∥AE.理由:∵CD⊥AD,DA⊥AB,∴∠CDA=∠DAB=90°,∵∠1=∠2,∴∠DAB-∠1=∠CDA-∠2,即∠DAE=∠ADF.∴DF∥AE(内错角相等,两直线平行)
?
?
?
?
9.(10分)如图所示,AC⊥BC于点C,∠1与∠2互余,这些条件能够判定哪两条直线平行?请说明理由.
解:AB∥CD.理由:∵AC⊥BC,∴∠ACB=90°.又∵∠1+∠2=90°,∴∠1+∠2+∠ACB=180°.即∠2+∠ACD=180°∴AB∥CD(同旁内角互补,两直线平行)
?第1章 平行线 第2课时 平行线的判定(二)10.(4分)如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA
B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC
D.∠BAC=∠ACD
11.(4分)如图,若∠3=∠4,则下列条件中,不能判定AB∥CD的是( )
A.∠1=∠2
B.∠1=∠3且∠2=∠4
C.∠1+∠3=90°且∠2+∠4=90°
D.∠1与∠2互补
12.(4分)如图,已知∠ACB=∠ABC,∠A=68°,则当∠ECB=____时,AB∥CE.
13.(9分)如图,
(1)由∠ABD=∠BDC,可得__
(2)由∠DBC=∠ADB,可得__;
(3)由∠CBE=∠DCB,可得
(4)由∠CBE=∠A,可得____;
)第1章 平行线 第2课时 平行线的判定(二)(5)由∠A+∠ADC=180°,可得__AB__∥__DC__;
(6)由∠A+∠ABC=180°,可得__AD__∥__BC__;
(7)由__∠DBA=∠E__,可得DB∥CE(同位角相等,两直线平行);
(8)由__∠DBC=∠BCE__,可得DB∥CE(内错角相等,两直线平行);
(9)由__∠DBE+∠E=180°(或∠BDC+∠DCE=180°)__,可得DB∥CE(同旁内角互补,两直线平行);
14.(9分)将一副三角板拼成如图
所示的图形,过点C作CF平分∠DCE
交DE于点F.说明CF∥AB的理由.
解:∵∠DCE=90°,CF平分∠DCE
∴∠DCF=∠ECF=45°,
又∵∠BAC=∠B=45°∴∠BAC=∠DCF,
∴CF∥AB(内错解相等,两直线平行)
??
15.(10分)如图所示,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,∠EDC+∠DCE=90°,试说明AD∥BC.
第1章 平行线 第2课时 平行线的判定(二)【综合运用】
16.如图,∠1=∠2,能判定AB∥DF吗?若不能判定AB∥DF,你认为还需要再添加一个什么样的条件?请说明理由.
解:不能判定AB∥DF;添加条件:∠CBD=∠EDB,∵∠CBD=∠EDB,∠1=∠2,∴∠CBD+∠1=∠EDB+∠2,即∠ABD=∠FDB,∴AB∥DF.
? 第1章 平行线 第2课时 平行线的性质(二) 1.(5分)直线c与a,b均相交,当a∥b时(如图),则( )
A.∠1>∠2 B.∠1<∠2C.∠1=∠2 D.∠1+∠2=90°
2.(5分)如图,已知AB∥CD,E是AB上一点,DE平分∠BEC交CD于点D,∠BEC=100°,则∠D的度数是( )
A.100° B.80° C.60° D.50°
3.(5分)下列图形中,由AB∥CD,能得到∠1=∠2的是( )
4.(5分)如图,已知AB∥CD,则图中与∠1互补的角有( )
A.2个 B.3个 C.4个 D.5个
第1章 平行线 第2课时 平行线的性质(二) 5.(5分)如图,直线a,b被直线c所截,下列说法正确的是( )
A.当∠1=∠2时,一定有a∥b
C.当a∥b时,一定有∠1=∠2
B.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°时,一定有a∥b
6.(5分)下列说法中正确的是( )
A.两直线被第三条直线所截得的同位角相等
B.两直线被第三条直线所截得的同旁内角互补
C.两平行线被第三条直线所截得的同位角的平分线互相垂直
D.两平行线被第三条直线所截得的同旁内角的平分线互相垂直
7.(5分)如图,AB∥CD,AD∥BE,试说明∠ABE=∠D.
解:∵AB∥CD(已知),
∴∠ABE=__ ).
∵AD∥BE(已知),
∴∠D=__ ),
∴∠ABE=∠D(等量代换).
8.(5分)如图,直线AB,CD被直线BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=____度.
9.(5分)如图,已知a∥b,小亮把三角板的直角顶点放在直线b上,
若∠1=40°,则∠2的度数为__
第1章 平行线 第2课时 平行线的性质(二) 10.(5分)已知三条不同的直线a,b,c在同一平面内,有下列四种说法:
①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中正确的是____ .(填序号)
?
11.(5分)如图,a∥b,∠1=65°,∠2=140°,则∠3=( )
A.100° B.105° C.110° D.115°
12.(5分)某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是( ) A.30° B.45° C.60° D.75°
13.(5分)如图所示,一只电子猫从A点出发,沿北偏东60°方向走了4 m到达B点,再从B点向南偏西15°方向走了3 m到达C点,那么∠ABC的度数为( )
A.45° B.75° C.105° D.135°
14.(5分)如图所示,C岛在A岛的北偏东50°方向上,
C岛在B岛的北偏西40°方向上,则从C岛看A,B两岛
的视角∠ACB等于____.
第1章 平行线 第2课时 平行线的性质(二)15.(8分)光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气中时,会发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的,如图所示,图中两条虚线与容器底面平行,∠1=45°,∠2=122°,求图中其他含有标号的角的度数.
解:∠3=45°,∠4=122°,∠5=58°,∠6=58°,
∠7=135°,∠8=135°
?
?
?
?16.(8分)如图所示,∠1=∠2,CE∥BF,试说明AB∥CD.
解:∵CE∥BF(已知),∴∠1=∠B(两直线平行,同位角相等)
∵∠1=∠2(已知),∴∠2=∠B,
∴AB∥CD
(内错角相等,两直线平行)
?
?
?
?
?
?
?
?
?
【综合运用】
17.(14分)如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以证明.
解:(1)∠P=360°-∠A-∠C; (2)∠P=∠A+∠C; (3)∠P=∠C-∠A; (4)∠P=∠A-∠C(证明略)
第1章 平行线 1.5 图形的平移 1.(5分)将如图所示的图案通过平移后可以得到下图中的( )
2.(5分)如图所示,图形B经过怎样的平移得到图形A( )
A.向上平移2个单位,向左平移4个单位
B.向上平移1个单位,向左平移4个单位
C.向上平移1个单位,向左平移8个单位
D.向上平移2个单位,向左平移8个单位
3.(5分)如图所示,下列关于△FDE平移得到△ABC的过程说法正确的是( )
A.沿射线EC的方向移动DB的长度
B.沿射线EC的方向移动CD的长度
C.沿射线BD的方向移动BD的长度
D.沿射线BD的方向移动DC的长度
4.(5分)如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是( )
A.40° B.50°C.90° D.130°
5.(5分)如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8
C.10 D.12
第1章 平行线 1.5 图形的平移 6.(5分)下列图形中,可由基本图形平移得到的是__ .(填图形编号)
7.(5分)如图,在梯形ABCD中,AD∥BC,现将DC平移到AE处,则DC∥____.
8.(5分)如图所示,△A′B′C′是由△ABC沿射线AC方向平移得到的,若AC=3 cm,则A′C′=____cm.
9.(10分)如图,平移正五边形ABCDE,使点A平移到
点A′,作出平移后的图形.
解:作图略
10.(6分)如图,直径为4 cm的⊙O1平移5 cm到⊙O2,
则图中阴影部分的面积为 __cm2.
?
第1章 平行线 1.5 图形的平移 11.(6分)某宾馆在重新装修后,准备在大厅的
楼梯上铺上某种红色地毯,已知这种地毯每平
方米售价30元,主楼梯道宽2米,其侧面如图
所示,则购买地毯至少需要__ __元.
12.(6分)如图,长为a m,宽为b m的一块草坪上修了一条1 m宽的笔直小路,则余下草坪的面积的可表示为__ m2;
现在为了增加美感,把这条小路改为宽恒为1 m的
弯曲小路,则此时余下草坪的面积为__ m2.
13.(10分)如图,方格中有一条美丽可爱的小金鱼.
(1)若方格的边长为1,则小鱼的面积为____;
(2)画出小鱼向左平移3格后的图形(不要求写作图步骤和过程).
解:(2)作图略
?
第1章 平行线 1.5 图形的平移 14.(10分)在平面上,七个边长均为1的等边三角形分别用①到⑦表示(如图).从④⑤⑥⑦组成的图形中,取出一个三角形,使剩下的图形经过一次平移,与①②③组成的图形拼成一个正六边形,你取出的是哪个三角形?写出平移的方向和平移的距离.
解:取出⑦,向上平移1个单位
?
?
?【综合运用】
15.(12分)操作与探究:
对数轴上的点P进行如下操作:先把点P表示的数乘 ,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.
点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′.如图,若点A表示的数是-3,则点A′表示的数是____;若点B′表示的数是2,则点B表示的数是____;已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合,则点E表示的数是多少? 检测内容:第1章 一、选择题(每小题4分,共40分)
1.把左图向上平移1个单位,再向左平移1个单位,所得图形是( )
2.如图所示,直线l与直线a,b相交,且a∥b,∠1=50°,则∠2的度数是( )
A.130° B.50° C.100° D.120°
3.如图,在下列条件中,能判定AB∥CD的是( )
A.∠1=∠3 B.∠2=∠3
C.∠1=∠4 D.∠3=∠4
4.下列说法错误的是( )
A.两条平行线被第三条直线所截,同位角的平分线互相平行
B.两条平行线被第三条直线所截,同旁内角的平分线互相平行
C.同一平面内,垂直于同一条直线的两直线平行
D.同一平面内无公共点的两直线必平行
5.如图所示,AE是∠FAB的平分线,且∠1=∠C,
则下列结论错误的是( )
A.AE∥BC B.∠2=∠ABC
C.∠C=∠ABC D.∠FAB+∠C=180°
6.如图所示,已知AB∥CD,直线l分别交AB,CD于点E,F.EG平分∠BEF,若∠EFG=40°.则∠EGF的度数是( ) A.60° B.70° C.80° D.90°
检测内容:第1章 7.将一直角三角板与两边平行的纸条按如图所示放置,有下列结论:(1)∠1=∠2;(2)∠3=∠4;(3)∠2+∠4=90°;(4)∠4+∠5=180°,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
8.如图所示,已知AB∥CD,则有( )
A.∠1=∠2+∠3 B.∠1=2∠2+∠3
C.∠1=2∠2-∠3 D.∠1=180°-∠2-∠3
9.如图所示,已知∠CAD=∠ACB,∠D=78°,则∠BCD等于( )
A.78° B.102°
C.120° D.无法确定
10.学习了平行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的,如图(1)~(4)所示,从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等;
②两直线平行,内错角相等;
③同位角相等,两直线平行;
④内错角相等,两直线平行.
A.①② B.②③ C.③④ D.①④
?
11.如图,将△ABC平移到△DEF的位置,则EF∥____.
检测内容:第1章 12.如图所示,l1∥l2,则∠1=__ __度.
13.两条平行线被第三条直线所截,同旁内角的度数比是7∶11,则这两个角的大小分别为__
70°,110°__.
14.如图所示,甲、乙两地之间要修一条公路,从甲地测得公路的走向是北偏东50°方向,如果甲、乙两地同时开工并使公路准确接通,那么在乙地应按∠a为__ __度的方向开工.
15.(10分)如图所示,已知∠1=∠2,若直线b⊥m,则直线a⊥m,请说明理由.
解:因为∠1=∠2(__已知__),
所以a∥b(__同位角相等,两直线平行两直线平行__),
所以∠3=∠4(__同位角相等__).
因为b⊥m(__已知__),
所以∠4=90°(__垂直定义__),
所以∠3=90°,所以a⊥m.
16.(10分)已知:如图,CD⊥AB,DE∥BC,∠1+∠2=180°.试说明FG⊥AB.
解:∵DE∥BC,∴∠1=∠DCB,又∵∠1+∠2=180°,
∴∠DCB+∠2=180°,∴CD∥GF,∵CD⊥AB,∴FG⊥AB
?
检测内容:第1章 17.(10分)如图所示,CD平分∠ACB,DE∥BC交AC于点E,
若∠ACB=50°,∠B=76°,求∠EDC及∠BDC的度数.
解:∵CD平分∠ACB,∠ACB=50°,∴∠BCD=∠ACD=25°,
∵DE∥BC∴∠BCD=∠EDC=25°,又∵∠B=76°,
∴∠BDC=180°-∠B-∠BCD=180°-76°-25°=79°
??
18.(14分)如图①所示是一根木尺折断后的情形,你可能注意过,木尺折断后的断口一般是参差不齐的,那么请你深入考虑一下其中所包含的一类数学问题,我们不妨取名叫“木尺断口问题”.
(1)如图②所示,已知AB∥CD,请问∠B,∠D,∠E有何关系并说明理由;
(2)如图③所示,已知AB∥CD,请问∠B,∠E,∠D又有何关系并说理由;
(3)如图④所示,已知AB∥CD,请问∠E+∠G与∠B+∠F+∠D有
何关系并说明理由.
解:(1)∠B+∠D=∠E,理由:过E作EM∥AB,根据平行线的传递性,则EM∥CD,∵EM∥AB∥CD,∴∠MEB=∠B,∠MED=∠D,∴∠B+∠D=∠E.
(2)∠B+∠E+∠D=360°.方法同(1)
(3)∠E+∠G=∠B+∠F+∠D,分别过E,F,G作AB的平行线,充分运用平行线的性质,得∠E+∠G=∠B+∠F+∠D.
?
?
A.∠2 B.∠3
C.∠4 D.∠5
2.(4分)如图, ∠CED和∠BDE是( )
A.同位角 B.内错角
C.同旁内角 D.互为补角
3.(4分)如图,与∠1是内错角的是( )
A.∠2 B.∠3
C.∠4 D.∠5第1章 平行线 1.2 同位角、内错角、同旁内角4.(4分)如图,若直线MN与△ABC的边AB,AC分别交于点E,F,则图中的内错角有( )
A.2对 B.4 C.6对 D.8对
5.(4分)下列图形中,∠1与∠2不是同位角的是( )
6.(4分)如图,∠B的同旁内角是
_∠BCD与∠BAD__.第1章 平行线 1.2 同位角、内错角、同旁内角7.(8分)如图所示,
(1)∠BED与∠CBE是直线__DE__、__BC__被直线__BE__所截成的__内错__角;
(2)∠A与∠CED是直线__AD__、__DE__被直线__AC__所截成的__同位__角;
(3)∠CBE与∠BEC是直线__BC__、__EC__被直线__BE__所截成的__同旁内__角;
(4)∠AEB与∠CBE是直线__AE__、__BC__被直线__BE__所截成的__内错__角.
8.(4分)如图所示,如果∠2=100°,那么∠1的同位角等于 ,∠1的内错角等于 ,∠1的同旁内角等于___
9.(4分)如图所示,已知∠1=∠4,请在括号内注明理由.
∵∠4+∠3=180°(___ _ ),
又∠1=∠4(__ _),
∴∠1+∠3=180°(__ __).第1章 平行线 1.2 同位角、内错角、同旁内角9.(4分)如图所示,已知∠1=∠4,请在括号内注明理由.
∵∠4+∠3=180°(__ __),
又∠1=∠4(__ __),
∴∠1+∠3=180°(__ __).
10.(10分)如图,试回答:
(1)∠1与∠2,∠3与∠4分别是具有怎样位置关系的角?
(2)当∠1=∠2时,∠3与∠4是具有怎样大小关系的角?
解:(1)∠1与∠2是同位角,∠3与∠4是同旁内角
(2)∠3与∠4互补
?第1章 平行线 1.2 同位角、内错角、同旁内角11.(6分)如图所示,请从“A.同位角;B.内错角;C.同旁内角;D.对顶角;E.以上都不是”中选出正确答案,并把它的代号填入题后的括号内.
(1)∠1与∠B是( );
(2)∠2与∠B是( );
(3)∠3与∠B是( );
(4)∠C与∠BAE是( );
(5)∠BAF与∠DAG是( );
(6)∠B与∠BAF是( ).
12.(4分)如图所示,直线l是l1与l2的截线.找出∠1的同位角,标上∠2,找出∠1的同旁内角,标上∠3.图中∠2、∠3的标法正确的是( )
13.(4分)如图所示,与∠α构成同位角的角的个数为( )
A.1个 B.2个
C.3个 D.4个14.(4分)如图,有下列6种说法:(1)∠1与∠4是内错角;(2)∠1与∠2是同位角;(3)∠2与∠4是内错角;(4)∠4与∠5是同旁内角;(5)∠2与∠4是同位角;(6)∠2与∠5是内错角.其中正确的有( C )
A.1个 B.2个 C.3个 D.4个第1章 平行线 1.2 同位角、内错角、同旁内角15.(10分)如图,Rt△ABC中,∠C=90°,DE⊥AC,交AB于点D,交AC于点E.
(1)说出当BC,DE被AB所截时,∠3的同位角、内错角和同旁内角.
(2)试说明∠1=∠2=∠3的理由.
解:(1)∠3的同位角是∠1,∠3的内错角是∠2,∠3的同旁内角是∠BDE (2)理由:∵∠C=90°,∴∠A+∠3=90°,∵DE⊥AC,∴∠A+∠1=90°,∴∠1=∠3,又∵∠1=∠2(对顶角),∴∠1=∠2=∠3
?
?
?
16.(12分)如图所示,指出图中∠1和∠A,∠3和∠A,∠2和∠B,∠BCD和∠B,∠3和∠B,∠A和∠B各是什么位置关系的角?并指出各是由哪两条直线被哪一条直线所截形成的角?
解:∠1和∠A是同位角,是由直线CE和AB被直线AD所截形成; ∠3和∠A是同旁内角,是由直线BC和AB被直线AD所截形成; ∠2和∠B是内错角,是由直线CE和AB被直线BC所截形成; ∠BCD和∠B是内错角,是由直线AD和AB被直线BC所截形成;∠3和∠B是同旁内角,是由直线AD和AB被直线BC所截形成; ∠A和∠B是同旁内角,是由直线AD和BC被直线AB所截形成
?
17.(10分)如图所示,在标出的7个角中,与∠1是内错角、同旁内角的各是哪几个?与∠5是同位角的是哪几个?
解:与∠1是内错角的有∠4,∠7;与∠1是同旁内角的有∠5,∠6;与∠5是同位角的有∠7
?第1章 平行线 第2课时 平行线的判定(二)1.(4分)如图所示,以下能判定GE∥CH的是( )
A.∠FEB=∠ECD B.∠AEG=∠DCH C.∠GEC=∠HCF D.∠HCE=∠AEG
2.(4分)如图所示,点E在AD的延长线上,下列条件中能判定BC∥AD的是( )
A.∠3=∠4 B.∠A+∠ADC=180° C.∠1=∠2 D.∠A=∠5
3.(4分)如图,下列判断错误的是( )
A.如果∠1=∠2,那么l3∥l4 B.如果∠3=∠5,那么l3∥l4
C.如果∠1=∠3,那么l3∥l4 D.如果∠2=∠3,那么l1∥l2
4.(4分)如图,下列给出的条件中,不能判定AB∥DF的是( )
A.∠A+∠2=180° B.∠A=∠3 C.∠1=∠4 D.∠1=∠A
第1章 平行线 第2课时 平行线的判定(二)5.(4分)如图,已知∠A=75°,∠B=105°,则AD____BC.
?
6.(4分)如图所示,点A在直线l上,如果∠B=75°,∠C=43°,那么当∠1=____°时,直线l∥BC;当∠2=____°时,直线l∥BC.
7.(6分)如图所示,
如果∠DBC=∠ADB,那么__;
如果∠ADC+∠DCB=180°,那么
如果∠CBE=__ __,那么AD∥BC;
如果∠CBE=__ _,那么AB∥CD.第1章 平行线 第2课时 平行线的判定(二)8.(10分)如图,已知CD⊥AD于点D,DA⊥AB于点A,∠1=∠2,则DF与AE平行吗?为什么?
解:DF∥AE.理由:∵CD⊥AD,DA⊥AB,∴∠CDA=∠DAB=90°,∵∠1=∠2,∴∠DAB-∠1=∠CDA-∠2,即∠DAE=∠ADF.∴DF∥AE(内错角相等,两直线平行)
?
?
?
?
9.(10分)如图所示,AC⊥BC于点C,∠1与∠2互余,这些条件能够判定哪两条直线平行?请说明理由.
解:AB∥CD.理由:∵AC⊥BC,∴∠ACB=90°.又∵∠1+∠2=90°,∴∠1+∠2+∠ACB=180°.即∠2+∠ACD=180°∴AB∥CD(同旁内角互补,两直线平行)
?第1章 平行线 第2课时 平行线的判定(二)10.(4分)如图,在下列条件中,能判断AD∥BC的是( )
A.∠DAC=∠BCA
B.∠DCB+∠ABC=180°
C.∠ABD=∠BDC
D.∠BAC=∠ACD
11.(4分)如图,若∠3=∠4,则下列条件中,不能判定AB∥CD的是( )
A.∠1=∠2
B.∠1=∠3且∠2=∠4
C.∠1+∠3=90°且∠2+∠4=90°
D.∠1与∠2互补
12.(4分)如图,已知∠ACB=∠ABC,∠A=68°,则当∠ECB=____时,AB∥CE.
13.(9分)如图,
(1)由∠ABD=∠BDC,可得__
(2)由∠DBC=∠ADB,可得__;
(3)由∠CBE=∠DCB,可得
(4)由∠CBE=∠A,可得____;
)第1章 平行线 第2课时 平行线的判定(二)(5)由∠A+∠ADC=180°,可得__AB__∥__DC__;
(6)由∠A+∠ABC=180°,可得__AD__∥__BC__;
(7)由__∠DBA=∠E__,可得DB∥CE(同位角相等,两直线平行);
(8)由__∠DBC=∠BCE__,可得DB∥CE(内错角相等,两直线平行);
(9)由__∠DBE+∠E=180°(或∠BDC+∠DCE=180°)__,可得DB∥CE(同旁内角互补,两直线平行);
14.(9分)将一副三角板拼成如图
所示的图形,过点C作CF平分∠DCE
交DE于点F.说明CF∥AB的理由.
解:∵∠DCE=90°,CF平分∠DCE
∴∠DCF=∠ECF=45°,
又∵∠BAC=∠B=45°∴∠BAC=∠DCF,
∴CF∥AB(内错解相等,两直线平行)
??
15.(10分)如图所示,已知点E在AB上,且CE平分∠BCD,DE平分∠ADC,∠EDC+∠DCE=90°,试说明AD∥BC.
第1章 平行线 第2课时 平行线的判定(二)【综合运用】
16.如图,∠1=∠2,能判定AB∥DF吗?若不能判定AB∥DF,你认为还需要再添加一个什么样的条件?请说明理由.
解:不能判定AB∥DF;添加条件:∠CBD=∠EDB,∵∠CBD=∠EDB,∠1=∠2,∴∠CBD+∠1=∠EDB+∠2,即∠ABD=∠FDB,∴AB∥DF.
? 第1章 平行线 第2课时 平行线的性质(二) 1.(5分)直线c与a,b均相交,当a∥b时(如图),则( )
A.∠1>∠2 B.∠1<∠2C.∠1=∠2 D.∠1+∠2=90°
2.(5分)如图,已知AB∥CD,E是AB上一点,DE平分∠BEC交CD于点D,∠BEC=100°,则∠D的度数是( )
A.100° B.80° C.60° D.50°
3.(5分)下列图形中,由AB∥CD,能得到∠1=∠2的是( )
4.(5分)如图,已知AB∥CD,则图中与∠1互补的角有( )
A.2个 B.3个 C.4个 D.5个
第1章 平行线 第2课时 平行线的性质(二) 5.(5分)如图,直线a,b被直线c所截,下列说法正确的是( )
A.当∠1=∠2时,一定有a∥b
C.当a∥b时,一定有∠1=∠2
B.当a∥b时,一定有∠1+∠2=90°
D.当∠1+∠2=180°时,一定有a∥b
6.(5分)下列说法中正确的是( )
A.两直线被第三条直线所截得的同位角相等
B.两直线被第三条直线所截得的同旁内角互补
C.两平行线被第三条直线所截得的同位角的平分线互相垂直
D.两平行线被第三条直线所截得的同旁内角的平分线互相垂直
7.(5分)如图,AB∥CD,AD∥BE,试说明∠ABE=∠D.
解:∵AB∥CD(已知),
∴∠ABE=__ ).
∵AD∥BE(已知),
∴∠D=__ ),
∴∠ABE=∠D(等量代换).
8.(5分)如图,直线AB,CD被直线BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=____度.
9.(5分)如图,已知a∥b,小亮把三角板的直角顶点放在直线b上,
若∠1=40°,则∠2的度数为__
第1章 平行线 第2课时 平行线的性质(二) 10.(5分)已知三条不同的直线a,b,c在同一平面内,有下列四种说法:
①如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;
③如果b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c.
其中正确的是____ .(填序号)
?
11.(5分)如图,a∥b,∠1=65°,∠2=140°,则∠3=( )
A.100° B.105° C.110° D.115°
12.(5分)某商品的商标可以抽象为如图所示的三条线段,其中AB∥CD,∠EAB=45°,则∠FDC的度数是( ) A.30° B.45° C.60° D.75°
13.(5分)如图所示,一只电子猫从A点出发,沿北偏东60°方向走了4 m到达B点,再从B点向南偏西15°方向走了3 m到达C点,那么∠ABC的度数为( )
A.45° B.75° C.105° D.135°
14.(5分)如图所示,C岛在A岛的北偏东50°方向上,
C岛在B岛的北偏西40°方向上,则从C岛看A,B两岛
的视角∠ACB等于____.
第1章 平行线 第2课时 平行线的性质(二)15.(8分)光线在不同介质中的传播速度是不同的,因此当光线从水中射向空气中时,会发生折射,由于折射率相同,所以在水中平行的光线,在空气中也是平行的,如图所示,图中两条虚线与容器底面平行,∠1=45°,∠2=122°,求图中其他含有标号的角的度数.
解:∠3=45°,∠4=122°,∠5=58°,∠6=58°,
∠7=135°,∠8=135°
?
?
?
?16.(8分)如图所示,∠1=∠2,CE∥BF,试说明AB∥CD.
解:∵CE∥BF(已知),∴∠1=∠B(两直线平行,同位角相等)
∵∠1=∠2(已知),∴∠2=∠B,
∴AB∥CD
(内错角相等,两直线平行)
?
?
?
?
?
?
?
?
?
【综合运用】
17.(14分)如图所示,已知AB∥CD,分别探索下列四个图形中∠P与∠A,∠C的关系,请你从所得的四个关系中任选一个加以证明.
解:(1)∠P=360°-∠A-∠C; (2)∠P=∠A+∠C; (3)∠P=∠C-∠A; (4)∠P=∠A-∠C(证明略)
第1章 平行线 1.5 图形的平移 1.(5分)将如图所示的图案通过平移后可以得到下图中的( )
2.(5分)如图所示,图形B经过怎样的平移得到图形A( )
A.向上平移2个单位,向左平移4个单位
B.向上平移1个单位,向左平移4个单位
C.向上平移1个单位,向左平移8个单位
D.向上平移2个单位,向左平移8个单位
3.(5分)如图所示,下列关于△FDE平移得到△ABC的过程说法正确的是( )
A.沿射线EC的方向移动DB的长度
B.沿射线EC的方向移动CD的长度
C.沿射线BD的方向移动BD的长度
D.沿射线BD的方向移动DC的长度
4.(5分)如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是( )
A.40° B.50°C.90° D.130°
5.(5分)如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
A.6 B.8
C.10 D.12
第1章 平行线 1.5 图形的平移 6.(5分)下列图形中,可由基本图形平移得到的是__ .(填图形编号)
7.(5分)如图,在梯形ABCD中,AD∥BC,现将DC平移到AE处,则DC∥____.
8.(5分)如图所示,△A′B′C′是由△ABC沿射线AC方向平移得到的,若AC=3 cm,则A′C′=____cm.
9.(10分)如图,平移正五边形ABCDE,使点A平移到
点A′,作出平移后的图形.
解:作图略
10.(6分)如图,直径为4 cm的⊙O1平移5 cm到⊙O2,
则图中阴影部分的面积为 __cm2.
?
第1章 平行线 1.5 图形的平移 11.(6分)某宾馆在重新装修后,准备在大厅的
楼梯上铺上某种红色地毯,已知这种地毯每平
方米售价30元,主楼梯道宽2米,其侧面如图
所示,则购买地毯至少需要__ __元.
12.(6分)如图,长为a m,宽为b m的一块草坪上修了一条1 m宽的笔直小路,则余下草坪的面积的可表示为__ m2;
现在为了增加美感,把这条小路改为宽恒为1 m的
弯曲小路,则此时余下草坪的面积为__ m2.
13.(10分)如图,方格中有一条美丽可爱的小金鱼.
(1)若方格的边长为1,则小鱼的面积为____;
(2)画出小鱼向左平移3格后的图形(不要求写作图步骤和过程).
解:(2)作图略
?
第1章 平行线 1.5 图形的平移 14.(10分)在平面上,七个边长均为1的等边三角形分别用①到⑦表示(如图).从④⑤⑥⑦组成的图形中,取出一个三角形,使剩下的图形经过一次平移,与①②③组成的图形拼成一个正六边形,你取出的是哪个三角形?写出平移的方向和平移的距离.
解:取出⑦,向上平移1个单位
?
?
?【综合运用】
15.(12分)操作与探究:
对数轴上的点P进行如下操作:先把点P表示的数乘 ,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.
点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′.如图,若点A表示的数是-3,则点A′表示的数是____;若点B′表示的数是2,则点B表示的数是____;已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合,则点E表示的数是多少? 检测内容:第1章 一、选择题(每小题4分,共40分)
1.把左图向上平移1个单位,再向左平移1个单位,所得图形是( )
2.如图所示,直线l与直线a,b相交,且a∥b,∠1=50°,则∠2的度数是( )
A.130° B.50° C.100° D.120°
3.如图,在下列条件中,能判定AB∥CD的是( )
A.∠1=∠3 B.∠2=∠3
C.∠1=∠4 D.∠3=∠4
4.下列说法错误的是( )
A.两条平行线被第三条直线所截,同位角的平分线互相平行
B.两条平行线被第三条直线所截,同旁内角的平分线互相平行
C.同一平面内,垂直于同一条直线的两直线平行
D.同一平面内无公共点的两直线必平行
5.如图所示,AE是∠FAB的平分线,且∠1=∠C,
则下列结论错误的是( )
A.AE∥BC B.∠2=∠ABC
C.∠C=∠ABC D.∠FAB+∠C=180°
6.如图所示,已知AB∥CD,直线l分别交AB,CD于点E,F.EG平分∠BEF,若∠EFG=40°.则∠EGF的度数是( ) A.60° B.70° C.80° D.90°
检测内容:第1章 7.将一直角三角板与两边平行的纸条按如图所示放置,有下列结论:(1)∠1=∠2;(2)∠3=∠4;(3)∠2+∠4=90°;(4)∠4+∠5=180°,其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
8.如图所示,已知AB∥CD,则有( )
A.∠1=∠2+∠3 B.∠1=2∠2+∠3
C.∠1=2∠2-∠3 D.∠1=180°-∠2-∠3
9.如图所示,已知∠CAD=∠ACB,∠D=78°,则∠BCD等于( )
A.78° B.102°
C.120° D.无法确定
10.学习了平行线后,小敏想出了过已知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的,如图(1)~(4)所示,从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等;
②两直线平行,内错角相等;
③同位角相等,两直线平行;
④内错角相等,两直线平行.
A.①② B.②③ C.③④ D.①④
?
11.如图,将△ABC平移到△DEF的位置,则EF∥____.
检测内容:第1章 12.如图所示,l1∥l2,则∠1=__ __度.
13.两条平行线被第三条直线所截,同旁内角的度数比是7∶11,则这两个角的大小分别为__
70°,110°__.
14.如图所示,甲、乙两地之间要修一条公路,从甲地测得公路的走向是北偏东50°方向,如果甲、乙两地同时开工并使公路准确接通,那么在乙地应按∠a为__ __度的方向开工.
15.(10分)如图所示,已知∠1=∠2,若直线b⊥m,则直线a⊥m,请说明理由.
解:因为∠1=∠2(__已知__),
所以a∥b(__同位角相等,两直线平行两直线平行__),
所以∠3=∠4(__同位角相等__).
因为b⊥m(__已知__),
所以∠4=90°(__垂直定义__),
所以∠3=90°,所以a⊥m.
16.(10分)已知:如图,CD⊥AB,DE∥BC,∠1+∠2=180°.试说明FG⊥AB.
解:∵DE∥BC,∴∠1=∠DCB,又∵∠1+∠2=180°,
∴∠DCB+∠2=180°,∴CD∥GF,∵CD⊥AB,∴FG⊥AB
?
检测内容:第1章 17.(10分)如图所示,CD平分∠ACB,DE∥BC交AC于点E,
若∠ACB=50°,∠B=76°,求∠EDC及∠BDC的度数.
解:∵CD平分∠ACB,∠ACB=50°,∴∠BCD=∠ACD=25°,
∵DE∥BC∴∠BCD=∠EDC=25°,又∵∠B=76°,
∴∠BDC=180°-∠B-∠BCD=180°-76°-25°=79°
??
18.(14分)如图①所示是一根木尺折断后的情形,你可能注意过,木尺折断后的断口一般是参差不齐的,那么请你深入考虑一下其中所包含的一类数学问题,我们不妨取名叫“木尺断口问题”.
(1)如图②所示,已知AB∥CD,请问∠B,∠D,∠E有何关系并说明理由;
(2)如图③所示,已知AB∥CD,请问∠B,∠E,∠D又有何关系并说理由;
(3)如图④所示,已知AB∥CD,请问∠E+∠G与∠B+∠F+∠D有
何关系并说明理由.
解:(1)∠B+∠D=∠E,理由:过E作EM∥AB,根据平行线的传递性,则EM∥CD,∵EM∥AB∥CD,∴∠MEB=∠B,∠MED=∠D,∴∠B+∠D=∠E.
(2)∠B+∠E+∠D=360°.方法同(1)
(3)∠E+∠G=∠B+∠F+∠D,分别过E,F,G作AB的平行线,充分运用平行线的性质,得∠E+∠G=∠B+∠F+∠D.
?
?
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
