1.5 三角全等的条件（2）

1.5三角形全等的条件（2）教案
一、教学目标
知识目标：探索并掌握三角形全等的条件之一“SAS”，并能应用它来判定两个三角形全等。理解线段垂直平分线的性质和概念。
能力目标：经历探索三角形全等条件的过程，体会利用操作、归纳获得数学结论的方法。
情感目标：培养学生合作探究的学习意识，增强学生的自信心。
二、教学重点、难点
重点：三角形全等的条件 “SAS”及应用。
难点： 例题教学(改编)
三、教学过程
（一）创设情境
小红为了测出池塘两端A，B的距离，她在地面上选择了点O，D，C，使OA=OC，OB=OD，且点A，O，C和点B，O，D都在一条直线上，小红量出DC=18米，她就知道AB的距离了， 你想知道为什么吗？
（二）探索新知
活动一：（1）画一画：
用量角器和刻度尺每人画一个三角形，使一个角为30°,且夹这个角的两条边分别为3cm和2cm.
（2）判一判：
小组内比较，所画的三角形是否全等。
（3）说一说：
①判定全等所用的方法（可能会有“SSS”、重叠等方法）。
②从中你得到了什么结论？
一般地，有一个角和夹这个角的两边对应相等的两个三角形全等（简写成“边角边”或“SAS”）。
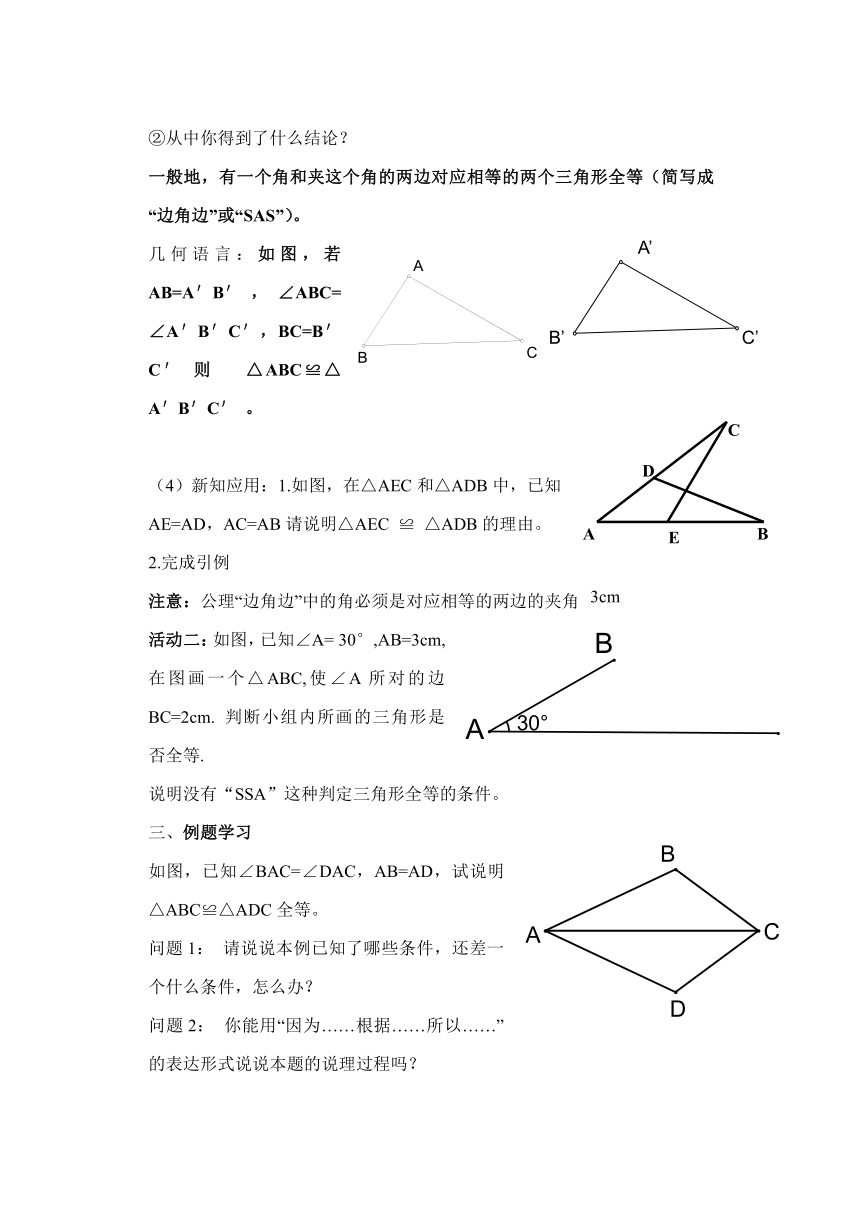
几何语言：如图，若 AB=A′B′ ， ∠ABC=∠A′B′C′，BC=B′C′ 则 △ABC≌△A′B′C′ 。
（4）新知应用：1.如图，在△AEC和△ADB中，已知AE=AD，AC=AB请说明△AEC ≌ △ADB的理由。
2.完成引例
注意：公理“边角边”中的角必须是对应相等的两边的夹角。
活动二：如图，已知∠A= 30°,AB=3cm,在图画一个△ABC,使∠A所对的边BC=2cm. 判断小组内所画的三角形是否全等.
说明没有“SSA”这种判定三角形全等的条件。
三、例题学习
如图，已知∠BAC=∠DAC，AB=AD，试说明△ABC≌△ADC全等。
问题1： 请说说本例已知了哪些条件，还差一个什么条件，怎么办？
问题2： 你能用“因为……根据……所以……”的表达形式说说本题的说理过程吗？
问题3： △ABC与△ADC全等了，你又能得到哪些结论？连接BD交AC于O，你能说明△BOC与△DOC全等吗？若全等，你又能得到哪些结论？
1.从中引出：垂直平分线定义
垂直于一条线段,并且平分这条线段的直线叫做这条线段的垂直平分线,简称中垂线
2.利用动画演示、几何说理得出：线段垂直平分线上的点到线段两端点的距离相等
几何语言：
∵ 点C在线段AB的中垂线上
∴ CA=CB
阐明：所得结论是说明两线段相等的一种重要方法。
四、巩固练习、延伸拓展
1、如图,AC是线段BD的垂直平分线,△ABC和△ADC全等吗 请说明理由.
2、如图,已知AB=CD,请你添加一个条件使得△ADC≌△CBA .
五、课堂小结
本节课你学习了什么？
发现了什么？
有什么收获？
本节课还存在什么没有解决的问题？
……
六、作业布置：见作业本
七、课后拓展
1.如图，已知AB⊥BD，
ED⊥CD，且AB=CD，
BC=DE，请问△ABC
是否全等于△CDE？AC
是否垂直于CE？为什么？
引伸：若将△CDE沿CB方向平移，且其余条件不变，则结 论AC1⊥C2E还成立吗？请说明理由。
D
C
B
A
O
C’
B’
A’
C
D
B
E
A
l
B
O
C
A
C
D
B
A
3cm
B
A
C
D