1.2同位角、内错角、同旁内角课件

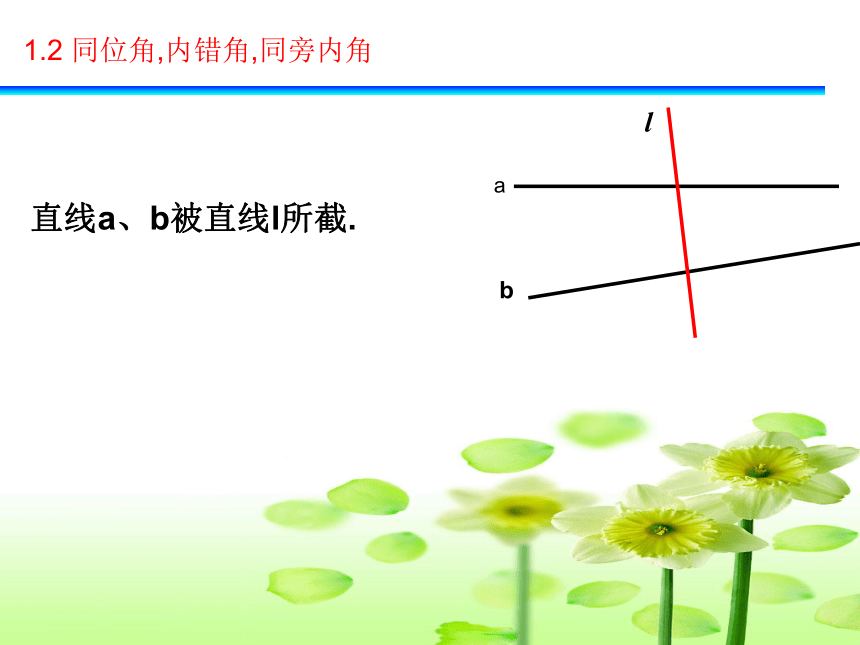
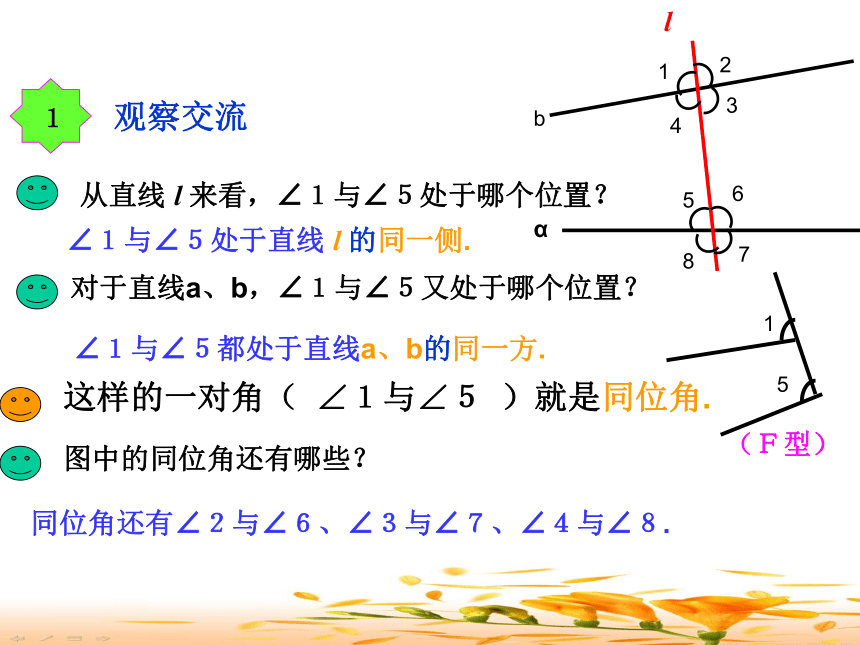
课件22张PPT。1.2 同位角,内错角,同旁内角中　　　山　　路中　　　山　　路平面上，两条直线有相交和平行两种位置关系.1.2 同位角,内错角,同旁内角直线a、b被直线l所截.1.2 同位角,内错角,同旁内角有4对对顶角, ∠2与∠4，∠5与∠7，∠6与∠8, ∠1和∠3分别是对顶角. 1.2 同位角,内错角,同旁内角直线a、b被直线l所截,有几对对顶角,它们分别是哪些角?∠１与∠５处于直线 l 的同一侧.∠１与∠５都处于直线a、b的同一方.同位角还有∠２与∠６、∠３与∠７、∠４与∠８.（Ｆ型）在形如字母“F”的图形中有同位角. 变式图形：图中的∠1与∠2都是同位角.二、探索交流三、类比交流∠4与∠6都处于直线 l 的两侧.∠4与∠6都处于直线a、b的内部.内错角还有∠3与∠5.（Z型）变式图形：图中的∠1与∠2都是内错角.图形特征：在形如“Z”的图形中有内错角.三、类比交流三、类比交流∠４与∠５处于直线 l 的同一侧.∠４与∠５都处于直线a、b的内部.同旁内角还有∠３与∠６.（n型）变式图形：图中的∠1与∠2都是同旁内角。图形特征：在形如“n”的图形中有同旁内角.　三、类比交流四、辩一辩两直线同侧两直线之间两直线之间在它的同旁在它的异侧在它的同侧 寻找同位角,内错角,同旁内角关键是什么？五、归纳小结
要分清哪两条直线和被第三条直线所截，
然后按相互的位置特征进行判别 .
例1 如图，直线DE截AB ，AC，构成8个角，
指出所有的同位角,内错角和同旁内角.
解：同位角是∠2与∠ 5 ，∠4与∠7， ∠1与∠8, ∠6和∠3；六、例题精讲 三线八角中同位角有4对,内错角有2对,同旁内有2对
内错角是∠4与∠5，∠1与∠6；同旁内角是∠1与∠5，∠4与∠6.
（3）归纳：两个角若有一边在同一直线上，这条直线就是截线，其余两边所在的直线是两直线（AB与DE 被AC所截，是内错角）∠A与∠6呢？∠A与∠5呢？（AB与DE 被AC所截，是同旁内角）（AB与DE 被AC所截，是同位角）（2）变式：∠A与∠8是哪两条直线被第3条直线所截的角？
它们是什么关系的角？
六、例题精讲解　　放　　路交通指南鞍马池路民人游乐场超市飞机场根据地图显示填空：学校与游乐场所在的角形成一（　　　）角
学校与超市所在的角形成一对（　　　　）角
学校与飞机场所在的角形成一对（　　　）角路练一练同位角同旁内角内错角解：因为∠1＝∠2（已知），∠2＝∠4（对顶角相等），所以∠1＝∠4. 因为∠2与∠3互补，所以∠2＋∠3＝180°，又因为∠1＝∠2，所以∠1＋∠3＝180°，
即∠1和∠3互补.例2 如图，直线DE交∠ABC的边BA于点F，如果∠1＝∠2，那么:
①同位角∠1和∠4相等，
②同旁内角∠1和∠3互补。
请说明理由.六、例题精讲F练一练：完成书本第8页作业题5七、课堂小结2、掌握辩别这些角的关键是看哪两条直线被哪一条直线所截、分清哪一条直线截哪两条直线形成了哪些角，是作出正确判定的前提，在截线的同旁找同位角，同旁内角，在截线的不同旁，找内错角，或者按不同字母类型进行分类（同位角“F”型，内错角“Z”型，同旁内角“n”型）。1、同位角、内错角、同旁内角都是两条直线被第三条直线所截时产生的，究其实质，它们主要是反映了直线相交产生的角中，相互位置所具有的特征：
(1) 同位角：具有“同上、同右”、“同上、同左”“同下、同右”或“同下、同左”
(2)内错角：同内、异侧
(3)同旁内角：同内、同侧八、布置作业作业本（2）及学习方法指导丛书
—— 1.2 同位角、内错角、同旁内角
预习 1.3 平行线的判定，完成相应预习内容