1.4 平行线的性质(2)课件

课件9张PPT。1.4 平行线的性质
（第2课时）如图，已知AG//CF，AB//CD，
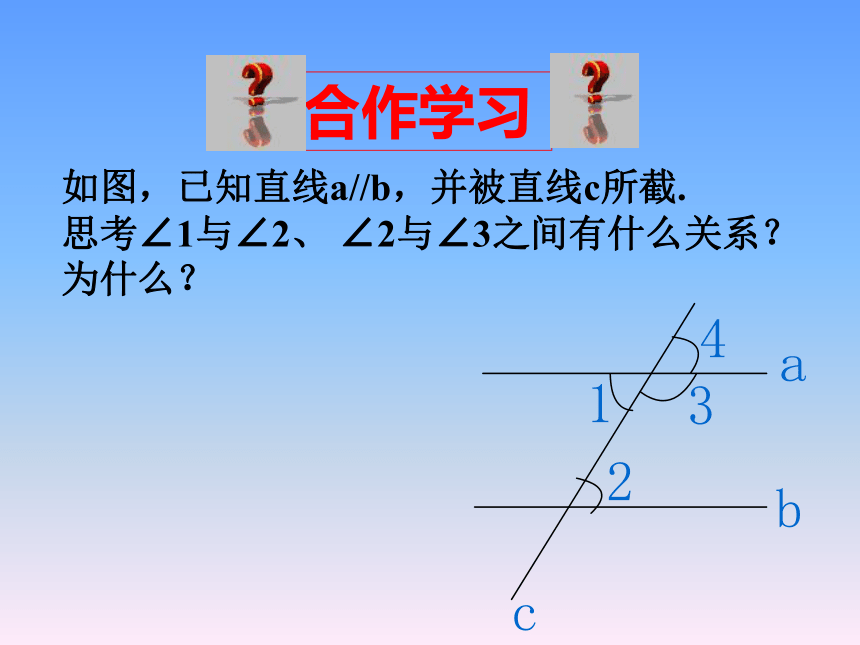
∠A＝40?，求∠C的度数。1解:∵ AG//CF(已知)∴ ∠A=∠1(两直线平行,同位角相等)又∵AB//CD(已知)∴ ∠1=∠C(两直线平行,同位角相等)∴ ∠A=∠C∵ ∠A＝40?∴ ∠C＝40?做一做合作学习如图，已知直线a//b，并被直线c所截.
思考∠1与∠2、 ∠2与∠3之间有什么关系？
为什么？
议一议性质两直线平行,内错角相等.
两直线平行,同旁内角互补. 两条平行直线被第三条直线所截，
内错角相等，同旁内角互补简记为:判定和性质的比较两条平行直线被第三条直线直线所截，互换。2、使用判定时是已知 ， 说明 。 角的相等或互补两直线平行 使用性质时是已知 ， 说明 。两直线平行角的相等或互补做一做例 1 如图所示，AB∥CD，AD∥BC，
判断∠1与∠2是否相等，并说明理由.
解： ∠1=∠2.理由如下：
∵AB∥CD（已知）
∴∠1+∠BAD=180°（两直线平行， 同旁内角互补）.
∵AD∥BC （已知）
∴∠2+∠BAD=180°（同理）.
∴∠1=∠2.
如图，已知 ∠1 =∠2
说明 ∠3 =∠4的理由.解：∵ ∠1 =∠2（已知） ∴a//b
(同位角相等,两直线平行) ∴ ∠3 =∠4
(两直线平行，内错角相等)变式练一练课本课内练习3例2 如图,已知∠ABC+∠C=1800,BD平分∠ABC,∠CBD与∠D相等吗? 请说明理由.解：∠CBD=∠D.
∵ ∠ABC+∠C=180°（已知）,
∴AB∥CD（同旁内角互补，两直线平行）.
∴∠D=∠ABD（两直线平行，内错角相等）.
又∴BD平分∠ABC,
所以∠CBD= ∠ABD= ∠D.ABCD作业题3、4作业作业本及学习方法指导丛书
—— 1.4 （2）平行线的性质
书本第18-19页课内练习1，2及作业题1,2
预习1.5图形的平移