5.1 同底数幂的乘法（2）

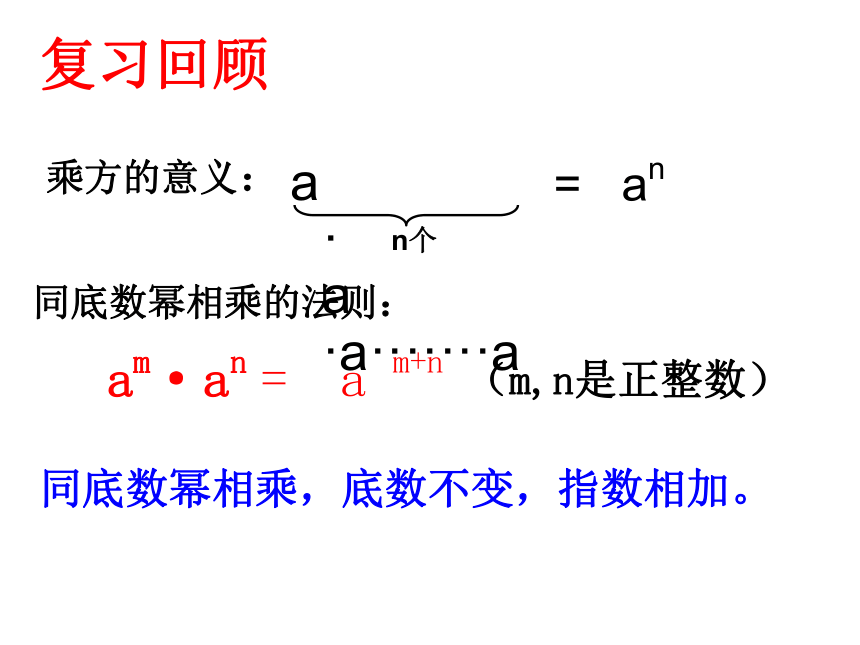
课件24张PPT。5.1 同底数幂的乘法（2）复习回顾a·a·a·······an个= an同底数幂相乘的法则：am·an = a m+n（m,n是正整数）乘方的意义：同底数幂相乘，底数不变，指数相加。练习： 如果这个正方体的棱长是 42 cm,那么它的体积是　　　cm3. 你知道 (42)3 是多少个 4 相乘吗?你知道吗？(42)3做一做合作学习：根据乘方的意义和同底数幂的乘法法则填空：计算下列各式，并说明理由
（1）（102）3 （2）（34）2
（3）（a3）5 （4）（am）n解（1）（102）3＝102×102×102（根据幂的意义）
＝102＋2＋2（根据同底幂相乘法则）
＝102×3
（2）（34）2＝34×34＝34＋4＝34×2=38
（3）（a3）5＝a3·a3·a3·a3·a3＝a3＋3＋3＋3＋3
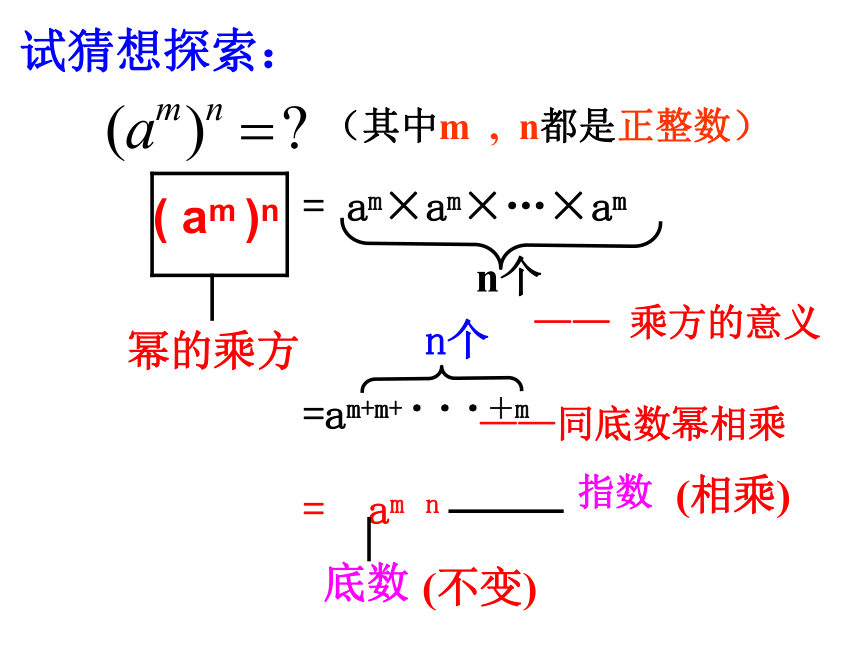
＝a3×5＝a15试一试 ( am )n= am×am×…×am=am+m+···＋mn个n个= am n底数(不变)(相乘)—— 乘方的意义——同底数幂相乘（其中m , n都是正整数）试猜想探索：幂的乘方法则：这就是说，（am）n与（an）m相等吗？为什么？请思考：解:= 10 7×3= 10212) (a4)83)(－53)34)[(－3)6]2= a 4×8= a 32= － 5 3×3=－5 9= (36)2=3 121)(107)35) － (y4)3 =－ y4×3 =－y126)[(a-b)3 ] 2=(a-b)3 ×2 =(a-b)6例1、计算：
1) (107)3 2) (a4)8
3) (－5 3)3 4) [(－3)6]2
5) －(y4)3 6) [(a-b)3]2⑴ (a2)4⑵(b3m)4⑶ (xn)m⑷ (b3)3⑸ x4·x4⑹ (x4)7
⑻ (a3)3⑽ (x6)5⑺ －(y7)2⑾ [(x+y)3]4⑼ [(－1)3]5 ⑿ [(a+1)3]n口答：抢答：⑵ (a3)6⑶ - (x5)2⑴ x4·x3⑷ [(x+y)3]4=x7=(x+y)12=a18=-x10 辨一辨：下面的计算对吗?如果不对 ,应怎样改正?
(43) 5 = 4 8
（-28）3= （-2）24
[(-3) 5 ] 3 = -315
(52 )4 ×5 = 58
（×） 415（×） 224（√） （×） 59练习：(口答)
1) (a3)4
2) a3·a4
3) ( y4)2
4) y4 · y 2
5) ( b m )2
6) b m · b 2= a7= b2m= b2+m= a12= y8= y6幂的乘方同底数幂相乘想一想：同底数幂的乘法法则与幂的乘方法则有什么相同点和不同点？幂的乘方法则：其中m , n都是正整数同底数幂的乘法法则：底数不变指数相乘指数相加其中m , n都是正整数练一练:1.填空:(用幂的形式表示结果)
(a3)4= ; a3.a4 = ;
(bm)2= ; x3+x3= ;
-(-y2)4= ; (x2n)2n= .2.计算下列各式,结果用幂的形式表示:
(73)4 (2)[(-10)3]5 (3)(a2)3.a4
(4) (b3)2+(b2)3 (5)-(-y2)5 (6)[(x+1)3]4a12a7b2m2x3-y8例2、计算：解：（1）原式=（2）原式=练一练:1、说出下面每一步计算理由,并将它们填入括号内:
(p2)3.(p5)2
=p6.p10 ( )
=p6+10 ( )
=p16幂的乘方法则同底数幂的乘法法则2、计算：
⑴ (a2)3 ⑵ a2·a3
⑶ (y5)5 ⑷ y5·y53、计算：
⑴ (x2)3· (x2)2 ⑵ (y3)4· (y4)3
⑶ －(xn)2· (x3)2m ⑷ (a2)3+a3 · a3课堂小结幂的乘方运算法则
（am）n＝amn（m，n都是正整数）
底数不变，指数相乘同底数幂相乘法则：
am·an＝am＋n（m，n都是正整数）
底数不变，指数相加拓展练习：1、若 am = 2, 则a3m =_____.
2、若 mx = 2, my = 3 ,
则 mx+y =____, m3x+2y =______.8672
⑴ 85＝2（ ）⑵ a12=(a3)( )
=(a2)( )
= a3 ·a( )注：幂运算性质均可逆向应用am·an=am+n(am) n=am n154693、填一填：4、在255，344，433，522，这四个幂的数值中，最大的一个是_______ 344 再 见 ！