5.4 乘法公式（1）

课件19张PPT。5.4 乘法公式（1）
---平方差公式 多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加.计算下列各题:
(a+2)(a-2)=________________
(3-x)(3+x)=________________
(a+b)(a-b )=________________
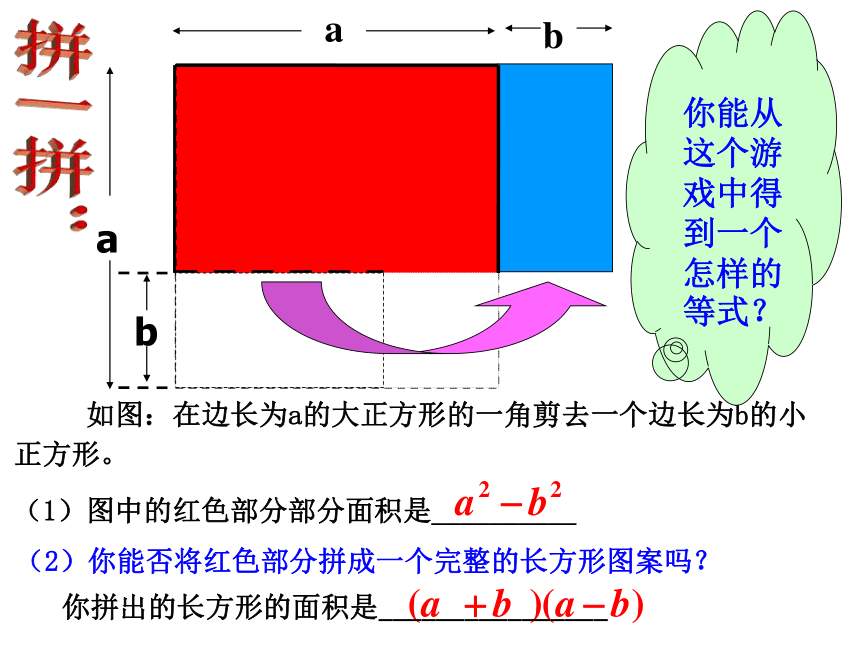
(4) (2m+n)(2m-n)=_______________ 比较等号两边的代数式,它们在系数和字母方面各有什么特点?你发现了什么规律？知识复习:(a+n)(b+m)=ab+nb+am+nm多项式与多项式相乘的法则:拼一拼： 如图：在边长为a的大正方形的一角剪去一个边长为b的小正方形。
（1）图中的红色部分部分面积是__________（2）你能否将红色部分拼成一个完整的长方形图案吗？你能从这个游戏中得到一个怎样的等式？你拼出的长方形的面积是________________(a+b)(a-b)=a2-b2即：两数和与这两数差的积，等于这两数的平方差 平方差公式 这里的字母a，b可以是数，或是单项式，甚至是更复杂的代数式下列式子中哪些可以用平方差公式运算?
⑴ (ab-8)(ab+8) ⑵⑶ (2+a)(a-2) ⑷ (3a+2b)(3a-2b)
⑸ (-4k+3)(-4k-3) ⑹ (1-x)(-x-1)
⑺ (-x-1)(x+1) ⑻ (x+3)(x-2)明察秋毫可以不可以可以可以可以可以可以不可以例1 运用平方差公式计算:
(1)(3x+5y)(3x-5y) =___2 – ___2 =____(3x)(5y)9x2-25y2 计算（口答）：
（1）（x+1)(x-1)
(2) (x+2)(x-2)
(3) (-m+n)(-m-n)
(4) (m+6)(m-6)
(5) (x+2y)(x-2y)
(6) (3x-2)(3x+2)
(7) (b+5a)(b-5a) = x2-1=(-m)2-n2=x2-(2y)2=x2-4y2=m2 - 6 2 = m2-36=(3x)2-22=9x2-4= X2 - 4= b2 - (5 a )2 =b2 - 25a 2 =m2-n2练习1：例2、用平方差公式计算:
103×97 =(100+3)(100-3)=1002-32=10000-9
=9991=(60-0.2)(60+0.2)=602-0.22
=3600-0.4
=3599.96(2)59.8×60.2运用平方差公式计算:练习2：2、5678×5680-56792=(5679-1)(5679+1)-56792=56792 -1 -56792= -1 例3、(a+b-c)(a-b-c)能用平方差公式运算吗?若能结果是哪两数的平方差?解：原式=[（a-c）+b][（a-c）-b]=（a-c）2-b2=a2-2ac+c2-b2例4、计算(1)1、利用平方差公式计算:
(2+1)(22+1)(24+1)(28+1)+1=(2-1)(2+1)(22+1)(24+1)(28+1)+1=(22-1)(22+1)(24+1)(28+1)+1=216练习3：2、(x-y)(x+y)(x2+y2)
3、已知 x2-y2=8 , x+y=-4 ，求x-y的值。4、如果A=1234567892,
B=123456788×123456790,
试比较A与B的大小.(数形结合思想和整体思想).1．通过本节课的学习活动，你们认识了什么？2．什么样的式子才能使用平方差公式？3.你会表述平方差公式的内容吗？ 会用字母写出它的表达式吗？4.还学到了哪些数学思想方法?2、如果(x+y-3)2+(x-y+5)2=0,求x2-y23、若m,n为有理数,式子
的值与n有关吗?试说明理由补充练习：1、运用平方差公式简便计算: 992 - 14、有两个正方形的周长之和为36cm，面积之差为72cm2,你能求出这两个正方形的边长吗？ 1、从前有一个狡猾的地主，他把一块长为x米的正方形的土地租给张老汉种植，有一天，他对张老汉说：“ 我把这块地的一边减少5米，另一边增加5米，继续租给你，你也没有吃亏，你看如何？” 张老汉一听觉得没有吃亏，就答应了 ，回到家中，他把这件事对邻居讲了，邻居一听，说：“张老汉你吃亏了！”，张老汉非常吃惊。同学们，你能告诉张老汉这是为什么吗？思维拓展：4×65×57×98×811×1312×122、观察并计算下列各组算式从以上的过程中你发现了什么规律？请用字母表示这一规律，你能说明它的正确性吗？=24=25=63=64=143=144思维拓展：再见