5.4 乘法公式(2)

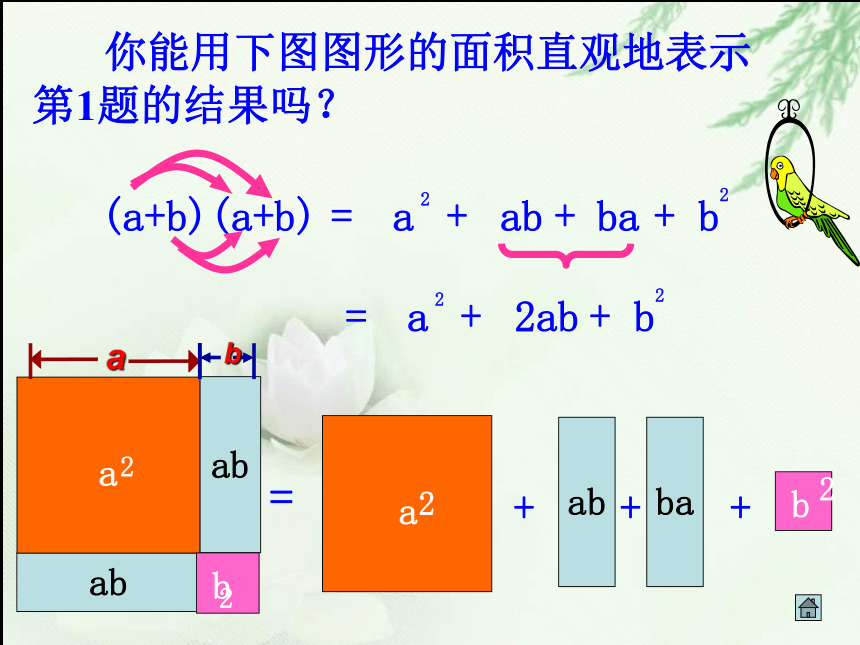
课件23张PPT。5.4乘法公式2你一定知道吧！两数和与这两数差的积
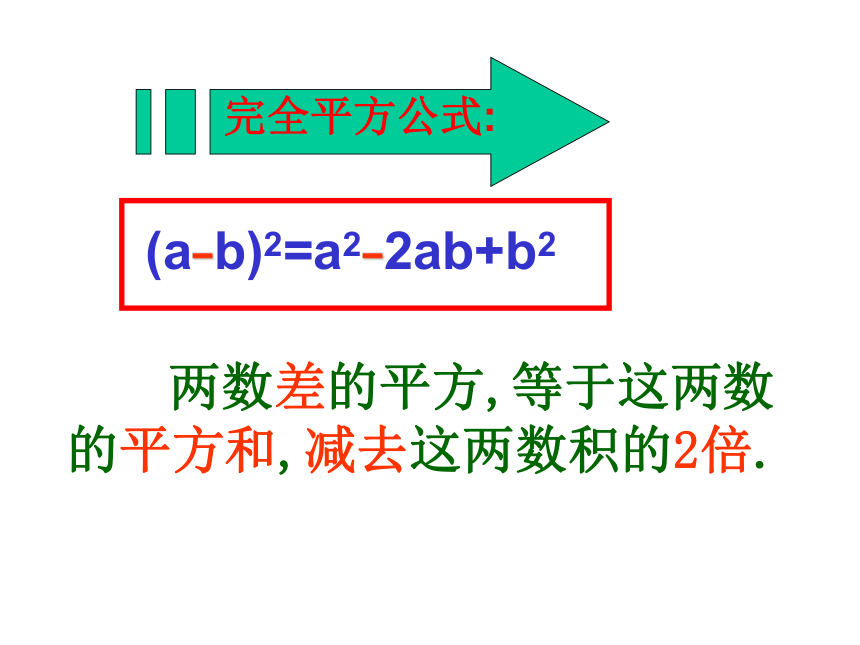
等于这两数的平方差.(a+b)(a—b)=a2—b2平方差公式试一试运用平方差公式计算:(1) (x+7)(x-7)(2) (2+a)(a-2)(3) (10s-3t)(10s+3t)(4) (-4x+y)(y+4x)(5) (-m+11)(-m-11) 运用多项式与多项式相乘的法则计算下列各式：1、(a+b)23、(2a+x)2 观察上述1、2两题的计算结果，你发现有什么规律？你能用你的发现来猜测第3题的结果吗？合 作 学 习=(a+b)(a+b)2、(2+x)2 =(2+x)(2+x)= 22+2x+2x+x2=(2a)2+2×2a?x+x2=a2+ab+ab+b2(a+b)(a+b)abba=+++=abba+++ 你能用下图图形的面积直观地表示第1题的结果吗？ 两数和的平方,等于这两数的平方和 , 加上这两数积的2倍. (a+b)2=a2+2ab+b2(2)(2a+3b)2= ( )2 + 2( )( ) + ( )2(a + 1)2=( )2+2( )( )+ ( )2aa112a2a3b3b用两数和的完全平方公式计算(填空):(a + b)2 = a2 + 2 a b + b2 你能用两数和的完全平方公式来计算(a?b)2吗?自主探索 ?=a2?2a b+b2=a2+2a (?b)+ (?b)2(a?b)2 =[a+(?b)]2 两数差的平方,等于这两数的平方和,减去这两数积的2倍. (a?b)2=a2?2ab+b2完全平方公式 平方差公式和完全平方公式也称乘法公式。( x )2 + 2 ? x ? 2y +(2y)2解：(2) (x+2y)2 = 例1 利用完全平方公式计算：
(2a－5)2 ； (2) (x+2y)2;
(3) (－2s+t)2; (4) (－3x－4y)2x2=+4xy+4y2(1)( a ? b )2 = a2 ? 2 a b + b2( 2 a ?5 )2=(2a)2?2·2a· 5+52= 4 a2_ 20a+25一分题4人小组竞赛！
二分题三分题四分题（优胜组将得到一定的加分）共5分共12分共8分共16分下列各式的计算错在哪里？应怎样改正？(1) (x+y)2 = x2 +y2(2) (a –b)2 = a2 -b2(4) (a+2b)2 = a2+2ab+2b2(3) (x– 1)2 = x2 – 2x (5) (2+x)2 = 2 + 4x+ x2请你直接应用完全平方公式计算：
1、（3+x)2 2、（y—7)2
3、（—2x—3y)2 4、（3— )2
选择适当的公式计算：（1）、（2x—1）（—1+2x）
（2）、（—2x—y）（2x—y）
（3）、 （—a+5）（—a—5）
（4）、（ab—1）（—ab+1）1、运用完全平方公式计算：992
活用公式:2、如果x2-6x+N是一个完全平方式,那么N是( )
(A)36 (B)9 (C)-36 (D)-93、用简便的方法计算:
1.232+2.46×0.77+0.772 (4)已知(a+b)2=11,ab=1,求(a-b)2的值.例2 一花农有4块正方
形茶花苗圃,边长分别
为 30.1 m , 29.5 m, 30m,
27m. 现将这4块苗圃的
边长都增加1.5m后,求各苗圃的面
积分别增加了多少m2?1、让我们一起体验收获的喜悦！
2、你认为今天的优胜组是谁? (a+b)2=a2+2ab+b2(a?b)2=a2?2ab+b2完全平方公式 两个数的和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍。首平方，尾平方，首尾两倍放中间本节课你学到了什么?注意完全平方公式和平方差公式不同： 完全平方公式的结果 是三项，即
(a ± b)2＝a2 ± 2ab + b2. 平方差公式的结果 是两项，即
(a+b)(a?b)＝a2?b2. 有时需要进行变形，使变形后的式子符合应
用完全平方公式的条件，即为“两数和(或差)
的平方”，然后应用公式计算. 在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2.作业 作业1、基础练习：见作业本
2、知识拓展：＜教与学＞。a2ababb2(a+b)2 =a?ba?bb(a?b)(a?b)2a2+2ab+b2即 (a?b)2 = a2?2ab+b2(a?b)2 = a2? ab ? b(a?b)　　　　　　试一试
　你能由两数和的完全平方公式的几何意义推想到两数差的完全平方公式的几何意义吗？例题例：利用完全平方公式计算：
(1) 0.982 (2) 10012解：(1) 原式 = （ 1 ? 0.02）2= 12 ? 2 ×1×0.02 + 0.022= 1 ? 0.04 + 0.0004= 0.9604（2）原式 = （ 1000 + 1 ）2= 10002 + 2 × 1000×1 + 12= 1000000 + 2000 + 1=1002001