5.2单项式的乘法

课件25张PPT。浙教版义务教育课程标准实验教科书5.2单项式的乘法一位旅行者用步长测量天安门广场的面积:他先从南走到北,记下所走的步数为1100步;再从东走到西,记下所走的步数为625步,然后根据自己的步长来估算广场的面积.如果该旅行者的步长用a表示,你能用含a的代数式表示广场的面积吗?假设这位旅行者的步长为0.8 ,那么广场的面积大约是多少?
计算 :-2abc3?3ab2=大胆尝试根据乘法交换律
和乘法结合律=-6a2b3c3根据同底数幂的乘法法则(-2×3)(a?a)(b?b2)?c35.2单项式的乘法各因式的系数结合成一组相同的字母结合一起一个字母法则：单项式与单项式相乘,把它们的系数、同
底数幂分别相乘，其余字母连同它的指数不变,
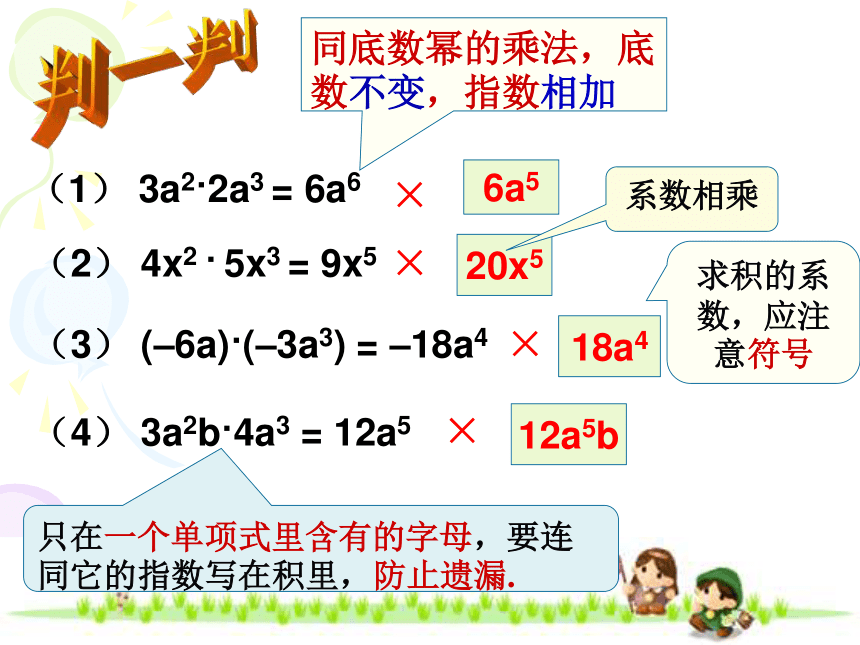
作为积的因式.大胆尝试注意事项 单项式与单项式相乘，把它们的系数、同底数幂分别相乘，其余字母连同它的指数不变,作为积的因式. (1) 3b? b2(4) (2×104)(6×103)?107(2) (－6ay3)(－a2) (3) (－3x)3?(5x2y)例1：计算例1:计算解:原式解:原式解:原式解:原式(5) －6a2b(x－y)3?2ab(x－y)2判一判 （1） 3a2?2a3 = 6a6 （2） 4x2 ? 5x3 = 9x5（3） (–6a)?(–3a3) = –18a4（4） 3a2b?4a3 = 12a5××××6a520x518a412a5b同底数幂的乘法，底数不变，指数相加求积的系数，应注意符号只在一个单项式里含有的字母，要连同它的指数写在积里，防止遗漏.
系数相乘(1) 3x ?4x=12x ( )(2) 7y2 ?8y3=56y6 ( )(3) (- 7m) (- 2m)2= - 28m3 ( )(4) (- 2a2b3)2 (- 3a3b2)=12a7b8 ( )判断下列计算是否正确,××
√×计算:(-2abc)?( ) 单项式与单项式相乘的法则: 单项式与单项式相乘,把它们的系数、同底数幂分别相乘，其余字母连同它的指数不变,作为积的因式.完成P112课内练习第3题
算一算（1） –3a?(2b)（3） (–2a)3?2ab2（2） 3x?(–5x2y)?(2xyz)ab一幅电脑画的尺寸如图:(1)请用两种不同的方式表示画面的面积.(2)这两种不同方式表示的面积应当相等,你能用运算律解释它们相等吗?(3)通过上面的讨论,你能总结出单项式与多项式相乘的运算规律吗?单项式与多项式相乘的法则: 单项式与多项式相乘,就是用单项式去乘多项式的每一项,,再把所得的积相加.a(b+c)=ab+ac例2 计算:
(1)
(2)注意: 1.注意多项式中每一项的符号; 注意单项式的符号
2. 积为一个多项式，其项数与多项式的项数相同,
不要漏乘了项。
3.积的符号的确定实质是：同号得正，异号得负例2:计算解:原式=解:原式=完成P112课内练习第3题(1) -m(a-b)=-ma-mb ( )(2) (a-3b)?(-6a)=-6a2-18ab ( )(3) (-x2y)(-9xy+1)=9x3y2+1( )(4) (2ab2-3ab)(-3ab)=-6a2b3+9a2b2 ( ) 判断下列计算是否正确,并简要说明理由.竞×××√大显身手填一填: (1) ( )?(3x2y2)=81x4y6(2) –3a2( –4ab+ )=–15a4+12a3b–3a227x2y4125a21(3) 若(my3)?(4yn)2=16y7
则m = , n = .
今天你学到了什么？感受 体会我学到了什么？1: 单项式与单项式相乘,把它们的 分
别相乘,其余 不变,作为积的因式2: 单项式与多项式相乘,就是用单项式去乘,
,再把所得的积相加系数、同底数幂字母连同它的指数多项式的每一项单项式乘以单项式单项式乘以多项式小结转化转化实数运算幂的运算转 化单项式乘以单项式单项式乘以多项式（1）已知：
则m= a= b= (2) 已知

(m是小于10的自然数)，则m= , n=___：挑战自我挑战自我已知求的值。 如图：在一个长方形的公园修建一个草坪,如阴影所示.E是AB的中点,F是BC的三等份点.已知AB=2a,BC=3b.求草坪的面积.继续尝试bann 下图是某教学楼的平面图你能用几种方法计算平面图的面积？课外作业1.作业本
2.教与学温馨提醒