第四章 二元一次方程组的复习课

课件19张PPT。二元一次方程组复习课1.下列方程中，哪些是二元一次方程？（1）2x-2y=5; (2)xy=3;
(3)x+y=0; (4)x2+x=1;
(5)3x-y=2z; (6)0.3x+0.5y=1.
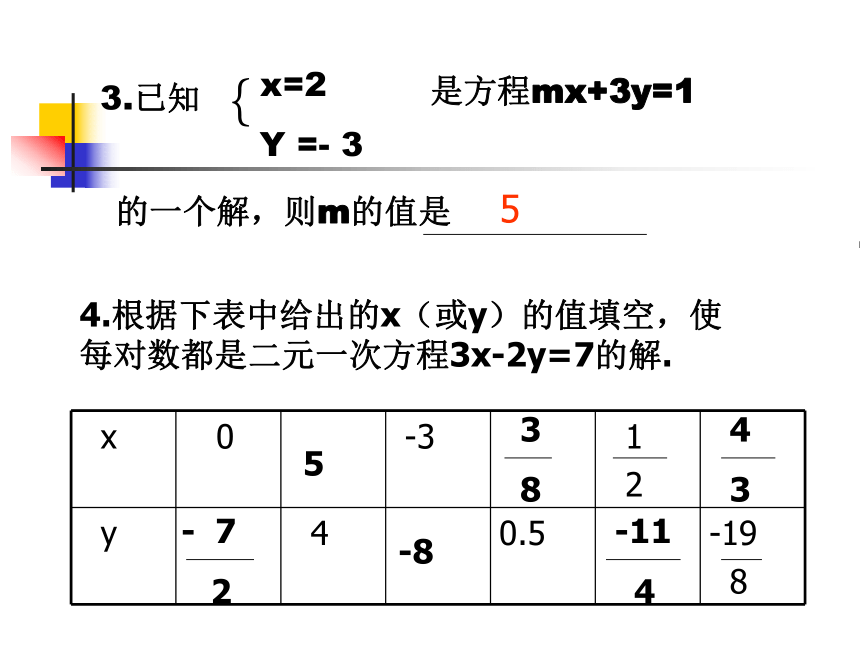
2.已知二元一次方程4x-7y=3.用关于x的代数式表示y，则y= ；用关于y的代数式表示x，则x= . x=2
Y =- 3｛3.已知 是方程mx+3y=1
的一个解，则m的值是4.根据下表中给出的x（或y）的值填空，使每对数都是二元一次方程3x-2y=7的解.5-85-11
43
84
3- 7
25、方程x+2y=7在正整数范围内的解有（ ）
A 1个 B 2个 C 3个 D 无数个C解后语：二元一次方程一般有无数个解，但它的解若受到限制往往
是有限个解。6.若x2m-1+5y3n-2m=7是二元一次方程，
则m= ，n= ， 11解后语：二元一次方程要求含有未知数项的次数都是1，同时未知数
项的系数不能为零。7、写出方程4x+y=10的自然数解　　（　　　　　）
8、请写出一个二元一次方程组，使它的解为：　 x=4 （　　　　　）
y=39.己知：


解方程组： 10.解方程组： 11.已知代数式x2+bx+c,当x=1时，它的值是2；当x=-1时，它的值是8，则b，c的值分别是（ ）
(A) b=3,c=-4. (B) b=-3,c=4.
(C) b=2,c=-5. (D) b=-2,c=5.B12.若方程组 的解也是方程3x+ky=10的解，则k的值是（ ）｛3x+5y=6
6x+15y=16B13.当a为何值时，方程组 的解x,y的值互为相反数？3x-5y=2a
2x+7y=a-18｛解：由x,y互为相反数，得x+y=0.即y=-x. ｛3x-5(-x)=2a
2x+7(-x)=a-18整理，得
代入原方程组，得3x-5(-x)=2a
2x+7(-x)=a-18｛解得 a=814.解下列方程组：｛｛｛｛（1） x=3y-2 (2) 2x=3y-1
Y=2x-y 4y=2x+1
(3) 3x-13y=-12 (4) 2x-5y+13=0
X+3y=2 9x+6y-8=0 解二元一次方程组的基本思路:二元一次方程消元转化(代入消元、加减消元)一元一次方程1. 如果一个两位数的十位数字为x，个位上的数字为y，那么这个两位数可表示为___________;如果交换个位和十位数字,得到的新两位数为________. 一个两位数的十位数字为x，个位上的数字为
y，如果在它们的中间加一个零,变成一个三位数,那么这个三位数可表示为___________.2. 两个两位数分别为x和y，如果将x放到y的左边就得到一个四位数,那么这个四位数可表示为___________;如果将x放到y的右边就得到一个新的四位数,那么这个新的四位数可表示为___________.10x+y10y+x100x+y100y+x100x+y问题二例 1 已知一个两位数，十位数字比
个位数字大3 ，将十位数字与个位
数字对调所得的新数比原数小27，
求这个两位数。若设十位数字为x，个位数字为y，则xy10x+yyx10y+x例2 两个两位数的和为 68，在较大的
两位数的右边接着写较小的两位数，得
到一个四位数；在较大的两位数的左边
接着写较小的两位数，也得到一个四位
数. 已知前一个四位数比后一个四位数
大2178, 求这两个两位数.若设较大的两位数为x，较小的两位数为y，则xy100x+yyx100y+x例3.小明骑摩托车在公路上高速行驶，12:00时看到里程碑上的数是一个两位数，它的数字之和是7；13:00时看里程碑上的两位数与12:00时看到的个位数和十位数颠倒了；14:00时看到里程碑上的数比12:00时看到的两位数中间多了个零，小明在12:00时看到里程碑上的数字是多少？解:设小明在12:00时看到的数的十位数字是x，个位的数字是y，那么答:小明在12:00时看到的数字是16.1.小明和小亮做游戏 ，小明在一个加数的
后面多写了上0，得到的和为242；小亮
在另一个加数后面多写了一个 0 ，得到
的和为341。原来的两个数分别为多少？试试看1456423061422902.根据下列数据信息，将统计表填写完整（精确到万户）
（1）2000年全国固定电话用户比移动电话用户多71.40%，
2002年全国固定电话用户比移动电话用户多3.64%；
（2）移动电话用户2002年比2000年增加了144.4%；固定电话
用户从1999年到2000年的实际增长数比从2001年到2002年的
实际增长数多206万户.849721523207673.为了有效地使用电力资源，某市电力局从元月起推出居民“峰谷”用电，若使用“峰谷”店、每天8：00　至22：00电费每千瓦时　0.56元（峰电价格），22：00至次日8：00电费为每千瓦时0.28元（谷电价格），不使用“峰谷”电的电费为每千瓦时0.53元，一个家庭使用“峰谷”电，某月电费为95.2元，经测算，比不使用“峰谷”电节约10.8元，问该家庭当月使用“峰电”和“谷电”各多少千瓦时？4.一条铁路线A，B，C三个车站的位置如图所示.已知 B，C两车站之间相距520千米.火车从B站出发，向C站方向匀速行驶，经过30分，距A站150千米；经过2时，距A站345千米.问火车从B站开出，多少时间后可到达C站？150千米520千米设火车的速度为x千米A，B两站之间的路程为y千米.345千米Y千米0.5x2x
其中理解问题指审题，搞清已知和未知，分析数量关系；
制订计划是指考虑如何根据等量关系设元，列出方程组;
执行计划是指列出方程组并求解，得到答案；
回顾反思是指回顾解题过程，检验答案的正确性以及是否符合题意。二元一次方程组解决实际问题的基本步骤：理解问题——制订计划——执行计划——回顾反思