5.1 同底数幂的乘法（3）

课件21张PPT。回顾:计算: 的底数是什么？
这是什么运算？
它表示什么？ 问题:请完成以下填空: =( ).( ).( )
=( ).( )
= =_________________
= =___________________
= 谈谈你发现的规律4×64×64×64×4×46×6×65.1 ③积的乘方
(ab)n= (ab) (ab) … (ab)
=(aa…a ) · ( bb… b )
=anbn 一般情况(ab)n (n为正整数),是否也有这种规律?请说明理由。 积的乘方,等于把积的每一个因式分别乘方,
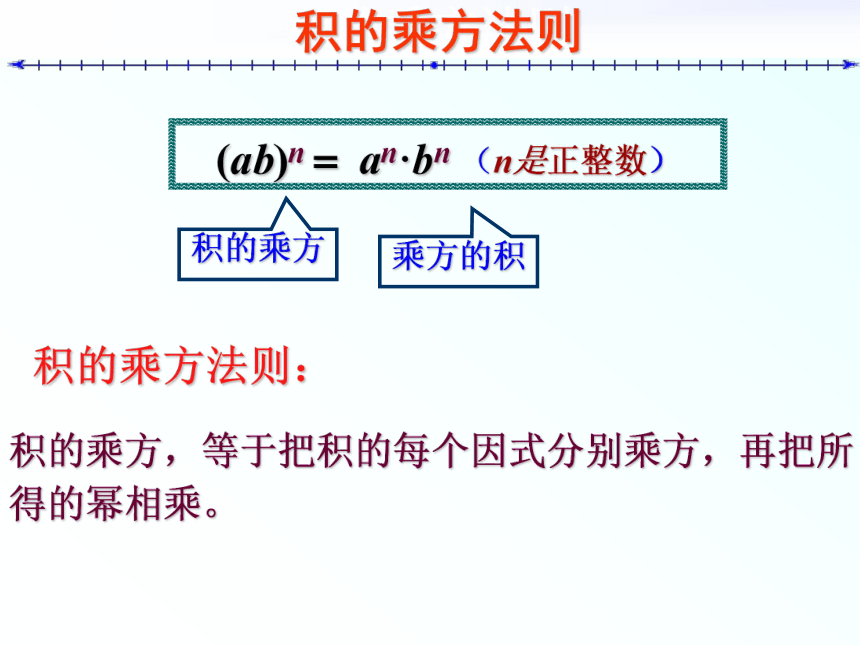
再把所得的幂相乘.积的乘方法则积的乘方，等于把积的每个因式分别乘方，再把所
得的幂相乘。 (ab)n = an·bn积的乘方乘方的积（n是正整数）积的乘方法则积的乘方法则：公 式 的 拓 展 三个或三个以上的积的乘方，是否也具有上面的性质?
怎样用公式表示?(abc)n=an·bn·cn=(ab)n·cn= an·bn·cn.例题解析例题解析 【例4】计算：
(1)(2b)5 ; (2)(3x3)6 ; (3)(-x3y2 )3 ; (4) =25b5 = 32b5 (1) (2b)5解：(2) (3x3)6 = 36 ( x3 ) 6= 36x18(3) (-x3 y2 ) 3 = -(x3 )3 ( y2 )3= - x9 y6(4) 阅读 ? 体验 ?= 729x18 注意:(1)分别乘方前,要看清各因式.
(2)因式可为数、单项式、多项式.
(3)对于底数有多个因式时此法则也适用.
如:(2a)3如:(2×3)4、[x(x+y)]5如:(abc)n=anbncn想一想:下面的计算对吗？错的请改正:××××××抢答填空:(1) (2)(3)(4) ( ) ( )( )( )做一做计算下列各式：例5.计算下列各式，结果用幂的形式表示:例题解析例题解析 【例6】木星是太阳系九大行星中最大的一颗，木星可以近似地看做球体。已知木星的半径大约是7×104 km，木星的体积大约是多少km3 ？（ p 取3.14）解： 阅读 ? 体验 ?=×(7×104)373×1012(km3)注意
运算顺序 !答：木星的体积大约是 1.44 ×1015 km3 ≈1436 ×1012
≈1.44 ×1015
能力挑战计算:(1)(4)(2)(3)随堂练习思 考：a 6y 3 ＝（ )3 81x 4y 10＝（ )2填空:(1)(2)(4)(3)( )( )( )( )学以至用例题：
你能口算2.58×48吗？结果是多少？ 2.59×48呢？由此你获得了什么启示？能力挑战 你能用简便的方法计算下列各题：（3）若am=3, an=2, 求a2m+n的值.本节课你的收获是什么？小结本节课你学到了什么?积的乘方法则的逆用：anbn＝（ab）n
（n是正整数）所学过的幂的运算性质有哪些?祝同学们 学习进步! 再 见