4.4二元一次方程组的应用(二)
图片预览




文档简介
课件16张PPT。4.4 二元一次方程组的应用(二)课前复习——
家具厂生产一种餐桌,1m3木材可做5张桌面或30条桌腿。现在有25m3木材,应怎样分配木材,才能使生产出来的桌面和桌腿恰好配套(一张桌面配4张桌腿)?共可生产多少张餐桌?解:方法一:设用xm3木材生产桌面,用ym3木材生产桌腿,根据题意得 例2:一根金属棒在0℃时的长度是q m,温度每升高1 ℃,它就伸长p m.当温度为t ℃时,金属棒的长度L可用公式L=pt+q计算.已测得当t=100 ℃时, L=2.002m;当t=500 ℃时,L=2.01m.
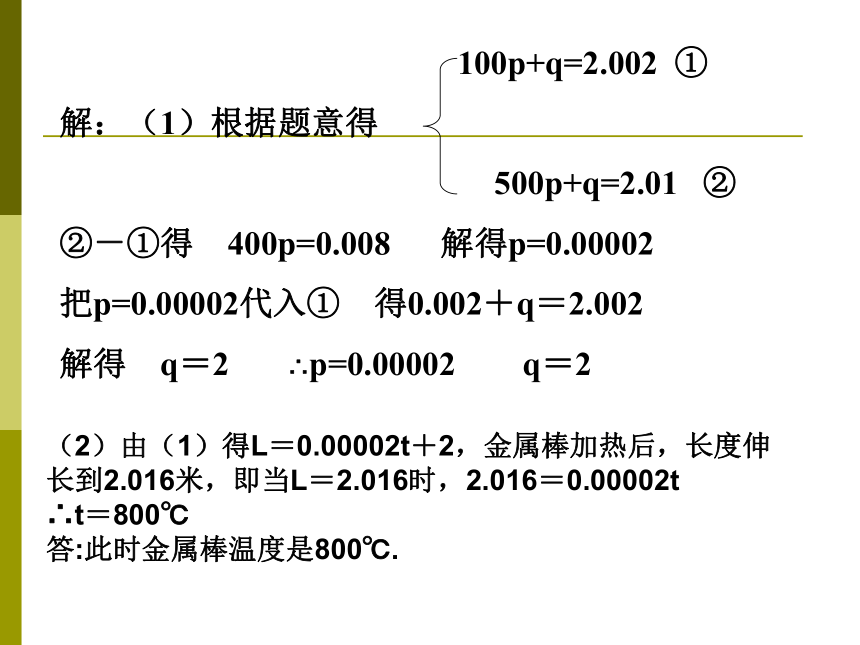
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少?(2)由(1)得L=0.00002t+2,金属棒加热后,长度伸长到2.016米,即当L=2.016时,2.016=0.00002t
∴t=800℃
答:此时金属棒温度是800℃.合作讨论讨论归纳:例2的解题步骤?
①代入(将已知的量 代入关系式)
②列(列出二元一次方程组)
③解(解这个二元一次方程组)
④回代(把求得p、q值重新回代到关系式中,使关系式只有两个相关的量,如只有L与t)
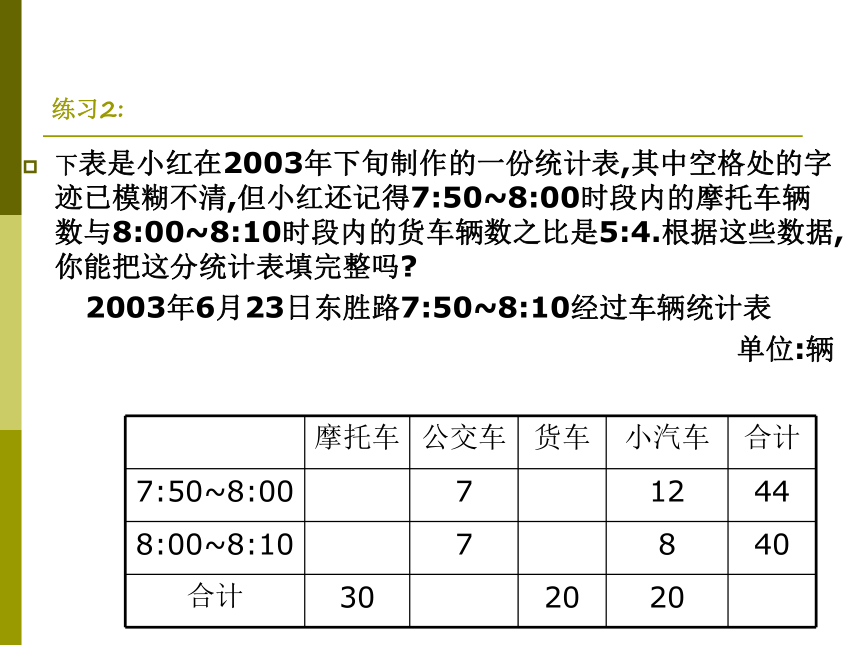
这种求字母系数的方法称为待定系数法 练习2:下表是小红在2003年下旬制作的一份统计表,其中空格处的字迹已模糊不清,但小红还记得7:50~8:00时段内的摩托车辆数与8:00~8:10时段内的货车辆数之比是5:4.根据这些数据,你能把这分统计表填完整吗?
2003年6月23日东胜路7:50~8:10经过车辆统计表
单位:辆例3:通过对一份中学生营养快餐的检测,得到以下信息:
(1)快餐总质量为300g;
(2)快餐的成分:蛋白质、碳水化合物、脂肪、矿物质;
(3)蛋白质和脂肪含量占50%;矿物质的含量是脂肪含量的2倍;蛋白质和碳水化合物含量占85%.
根据上述数据回答下面的问题:
①分别求出营养快餐中蛋白质、碳水化合物、脂肪、 矿物质的质量和所占百分比;
②根据计算结果制作扇形统计图表示营养成分的信息。
方法一:设营养快餐中蛋白质x克,碳水化合物y克,脂肪z克,矿物质t克
由题意得:
(1)设一份营养快餐中含蛋白质xg,脂肪yg,则矿物质为2yg,碳水化合物为(300×85%-x)g,由题意得
x+y=300×50%
(300×85%-x)+2y=300×50%
解得 y=15
所以x=135从而可知蛋白质的含量为135g、脂肪的含量15g、矿物质的含量30g、碳水化合物的含量120g。方法二中学生营养快餐成分统计表复习绘制扇形统计图的步骤有那些?1、计算各部分所占的百分比
2、计算各个扇形的圆心角度数
3、在圆中画出各个扇形并标上相应的项目和百分比
4、注明统计图名称 回顾反思检验所求答案是否符合题意
反思本例对我们有什么启示? 解信息量大,关系复杂的实际问题时,要仔细分析题意,找出等量关系,
利用它们的数量关系适当地设元,然后列方程组解题。谈谈你的收获1、如何求一些公式中的字母系数(待定系数法)它的一般步骤是怎样的?
2、怎样解决一些信息量大,关系比较复杂的实际问题?小明骑摩托车在公路上匀速行驶,12:00时看到里程碑上的数是一个两位数,它的数字之和是7;13:00时看里程碑上的两位数与12:00时看到的个位数和十位数颠倒了;14:00时看到里程碑上的数比12:00时看到的两位数中间多了个零,小明在12:00时看到里程碑上的数字是多少?解:设小明在12:00时看到的数的十位数字是x,个位的数字是y,那么答:小明在12:00时看到的数字是16思考:两地相距280千米,一轮船在其间航行,顺流用了14小时,逆流用了20小时,求轮船在静水中的速度和水流的速度.
家具厂生产一种餐桌,1m3木材可做5张桌面或30条桌腿。现在有25m3木材,应怎样分配木材,才能使生产出来的桌面和桌腿恰好配套(一张桌面配4张桌腿)?共可生产多少张餐桌?解:方法一:设用xm3木材生产桌面,用ym3木材生产桌腿,根据题意得 例2:一根金属棒在0℃时的长度是q m,温度每升高1 ℃,它就伸长p m.当温度为t ℃时,金属棒的长度L可用公式L=pt+q计算.已测得当t=100 ℃时, L=2.002m;当t=500 ℃时,L=2.01m.
(1)求p,q的值;
(2)若这根金属棒加热后长度伸长到2.016m,问这时金属棒的温度是多少?(2)由(1)得L=0.00002t+2,金属棒加热后,长度伸长到2.016米,即当L=2.016时,2.016=0.00002t
∴t=800℃
答:此时金属棒温度是800℃.合作讨论讨论归纳:例2的解题步骤?
①代入(将已知的量 代入关系式)
②列(列出二元一次方程组)
③解(解这个二元一次方程组)
④回代(把求得p、q值重新回代到关系式中,使关系式只有两个相关的量,如只有L与t)
这种求字母系数的方法称为待定系数法 练习2:下表是小红在2003年下旬制作的一份统计表,其中空格处的字迹已模糊不清,但小红还记得7:50~8:00时段内的摩托车辆数与8:00~8:10时段内的货车辆数之比是5:4.根据这些数据,你能把这分统计表填完整吗?
2003年6月23日东胜路7:50~8:10经过车辆统计表
单位:辆例3:通过对一份中学生营养快餐的检测,得到以下信息:
(1)快餐总质量为300g;
(2)快餐的成分:蛋白质、碳水化合物、脂肪、矿物质;
(3)蛋白质和脂肪含量占50%;矿物质的含量是脂肪含量的2倍;蛋白质和碳水化合物含量占85%.
根据上述数据回答下面的问题:
①分别求出营养快餐中蛋白质、碳水化合物、脂肪、 矿物质的质量和所占百分比;
②根据计算结果制作扇形统计图表示营养成分的信息。
方法一:设营养快餐中蛋白质x克,碳水化合物y克,脂肪z克,矿物质t克
由题意得:
(1)设一份营养快餐中含蛋白质xg,脂肪yg,则矿物质为2yg,碳水化合物为(300×85%-x)g,由题意得
x+y=300×50%
(300×85%-x)+2y=300×50%
解得 y=15
所以x=135从而可知蛋白质的含量为135g、脂肪的含量15g、矿物质的含量30g、碳水化合物的含量120g。方法二中学生营养快餐成分统计表复习绘制扇形统计图的步骤有那些?1、计算各部分所占的百分比
2、计算各个扇形的圆心角度数
3、在圆中画出各个扇形并标上相应的项目和百分比
4、注明统计图名称 回顾反思检验所求答案是否符合题意
反思本例对我们有什么启示? 解信息量大,关系复杂的实际问题时,要仔细分析题意,找出等量关系,
利用它们的数量关系适当地设元,然后列方程组解题。谈谈你的收获1、如何求一些公式中的字母系数(待定系数法)它的一般步骤是怎样的?
2、怎样解决一些信息量大,关系比较复杂的实际问题?小明骑摩托车在公路上匀速行驶,12:00时看到里程碑上的数是一个两位数,它的数字之和是7;13:00时看里程碑上的两位数与12:00时看到的个位数和十位数颠倒了;14:00时看到里程碑上的数比12:00时看到的两位数中间多了个零,小明在12:00时看到里程碑上的数字是多少?解:设小明在12:00时看到的数的十位数字是x,个位的数字是y,那么答:小明在12:00时看到的数字是16思考:两地相距280千米,一轮船在其间航行,顺流用了14小时,逆流用了20小时,求轮船在静水中的速度和水流的速度.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
