浙教版七年级数学下学期期末专项复习 专题01平行线(含解析)
文档属性
| 名称 | 浙教版七年级数学下学期期末专项复习 专题01平行线(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 430.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-10-29 12:41:16 | ||
图片预览

文档简介
专题01 平行线-七年级数学下学期期末专项复习(浙教版)
专题01 平行线
注意事项∶
1. 答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上.
2. 所有答案都必须写到答题卷上.选择题必须使用2B铅笔填涂;非选择题必须使用黑色字迹的签字笔或钢笔书写,字体要工整,笔迹要清楚.
3.本试卷分试题卷和答题卷两部分,满分100分.考试时间共90分钟.
一、单选题(共30分)
1.下列说法正确的个数有( )
①同位角相等;②过一点有且只有一条直线与已知直线垂直;③过一点有且只有一条直线与已知直线平行;④若a∥b,b∥c,则a∥c.
A.1个 B.2个 C.3个 D.4个
2.如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
A.同位角 B.内错角
C.同旁内角 D.对顶角
3.下列图形中,可以由其中一个图形通过平移得到的是( )
A. B. C. D.
4.如图,能判定EB∥AC的条件是( )
A.∠C=∠1 B.∠A=∠2
C.∠C=∠3 D.∠A=∠1
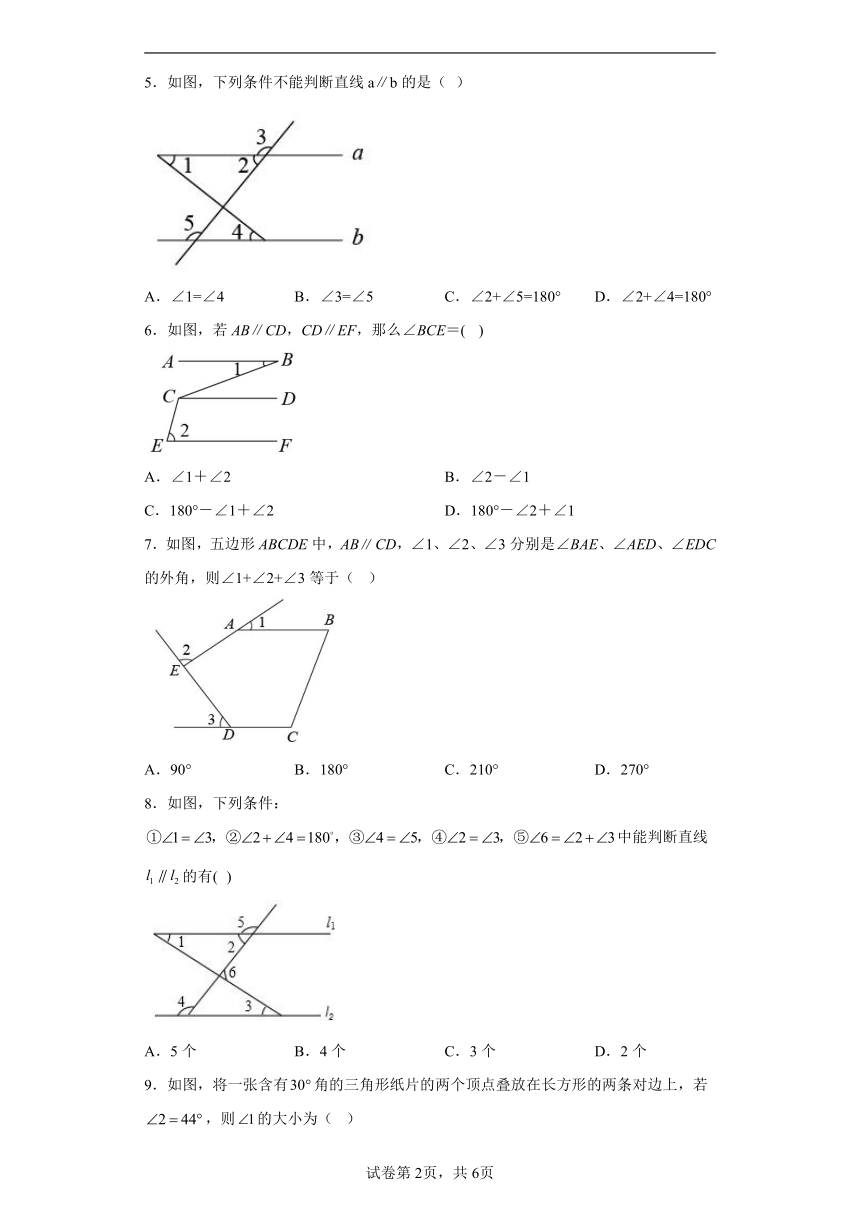
5.如图,下列条件不能判断直线a∥b的是( )
A.∠1=∠4 B.∠3=∠5 C.∠2+∠5=180° D.∠2+∠4=180°
6.如图,若AB∥CD,CD∥EF,那么∠BCE=( )
A.∠1+∠2 B.∠2-∠1
C.180°-∠1+∠2 D.180°-∠2+∠1
7.如图,五边形ABCDE中,ABCD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )
A.90° B.180° C.210° D.270°
8.如图,下列条件:中能判断直线的有( )
A.5个 B.4个 C.3个 D.2个
9.如图,将一张含有角的三角形纸片的两个顶点叠放在长方形的两条对边上,若,则的大小为( )
A. B. C. D.
10.如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.102° B.108° C.124° D.128°
二、填空题(共21分)
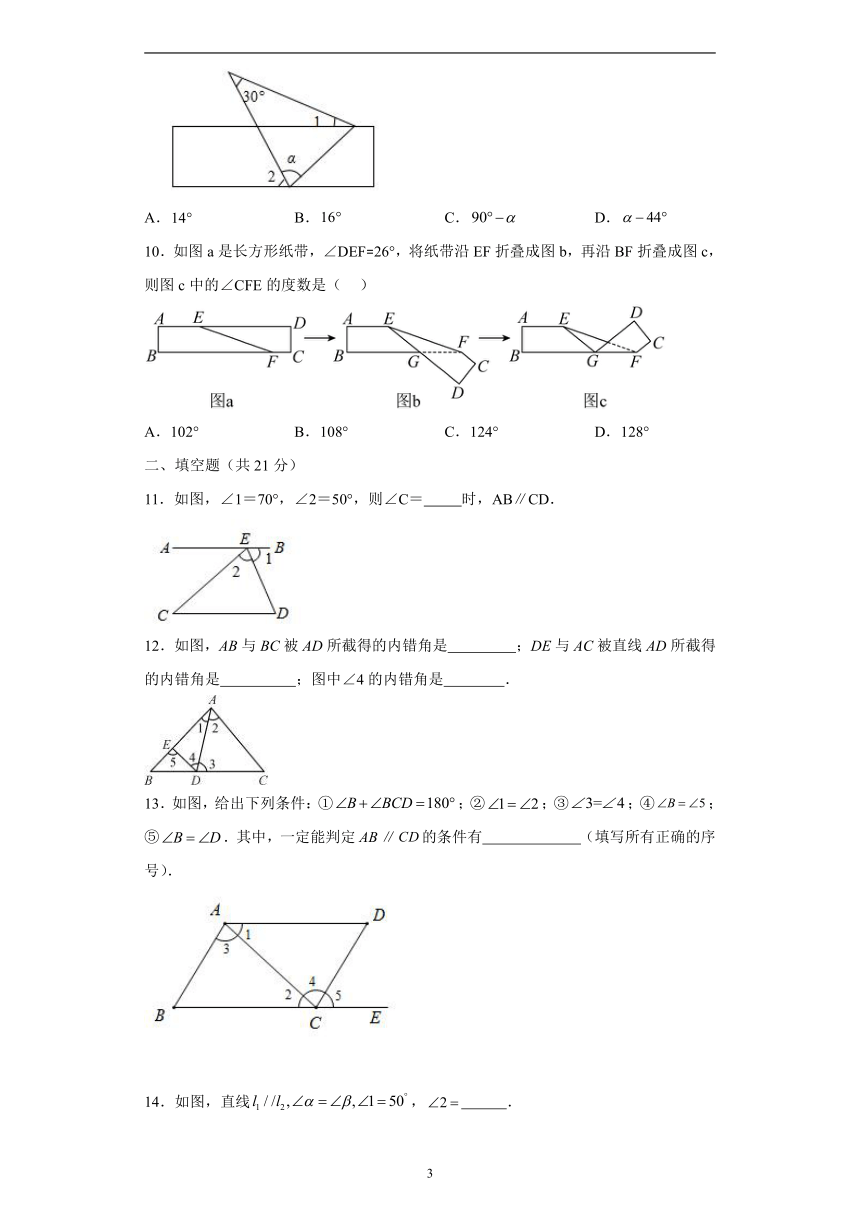
11.如图,∠1=70°,∠2=50°,则∠C= 时,AB∥CD.
12.如图,AB与BC被AD所截得的内错角是 ;DE与AC被直线AD所截得的内错角是 ;图中∠4的内错角是 .
13.如图,给出下列条件:①;②;③;④;⑤.其中,一定能判定∥的条件有 (填写所有正确的序号).
14.如图,直线, .
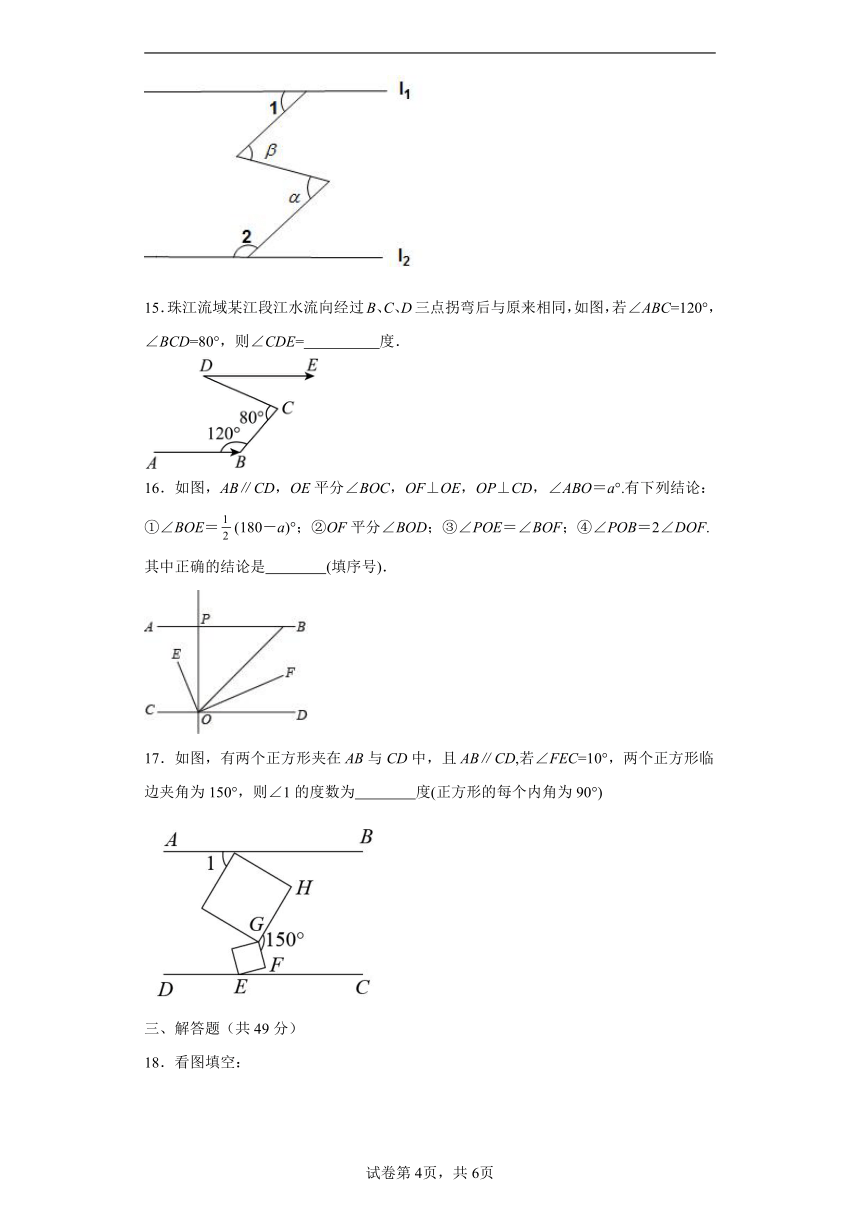
15.珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE= 度.
16.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.有下列结论:①∠BOE=(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的结论是 (填序号).
17.如图,有两个正方形夹在AB与CD中,且AB∥CD,若∠FEC=10°,两个正方形临边夹角为150°,则∠1的度数为 度(正方形的每个内角为90°)
三、解答题(共49分)
18.看图填空:
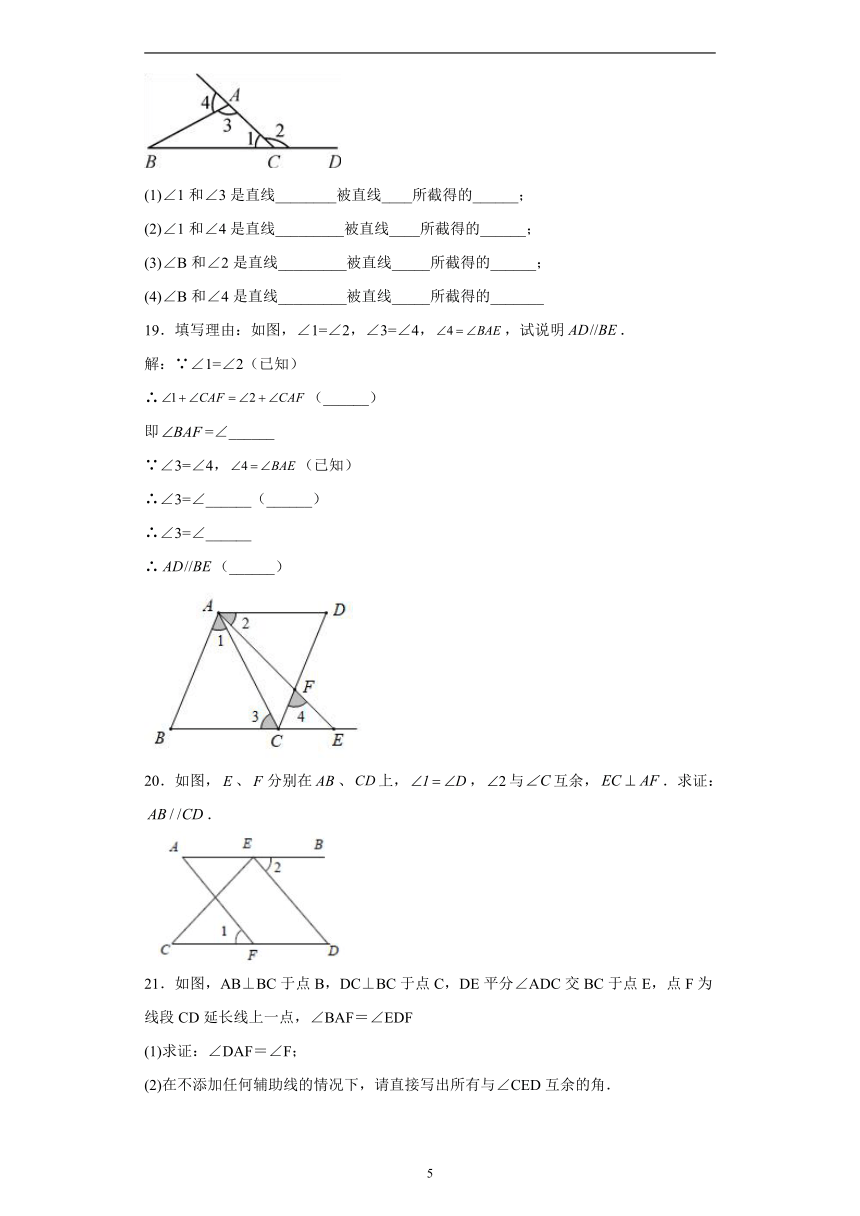
(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
19.填写理由:如图,∠1=∠2,∠3=∠4,,试说明.
解:∵∠1=∠2(已知)
∴(______)
即=∠______
∵∠3=∠4,(已知)
∴∠3=∠______(______)
∴∠3=∠______
∴(______)
20.如图,、分别在、上,,与互余,.求证:.
21.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF
(1)求证:∠DAF=∠F;
(2)在不添加任何辅助线的情况下,请直接写出所有与∠CED互余的角.
22.如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D,
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
23.一、问题情境:在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含角的直角三角尺”为主题开展数学活动.
二、操作发现:
(1)如图1,小明把三角尺的角的顶点G放在CD上,若,求的度数;
(2)如图2,小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明与之间的数量关系;
三、结论应用:
(3)如图3,小亮把三角尺的直角顶点F放在CD上,角的顶点E落在AB上.若,求的度数用含的式子表示.
参考答案:
1.A
【分析】根据平行线的性质,垂线的性质和平行公理对各个说法分析判断后即可求解.
【详解】解:①如图,直线AB、CD被直线GH所截,∠AGH与∠CHF是同位角,但它们不相等,故说法错误;
②同一平面内,过一点有且只有一条直线与已知直线垂直,说法错误;
③应为过直线外一点有且只有一条直线与已知直线平行,故说法错误;
④平行于同一直线的两条直线平行,是平行公理的推论,故说法正确.
综上所述,正确的说法是④共1个.
故选A.
【点睛】本题考查了平行线的性质,垂线的性质和平行公理,是基础知识,熟练掌握各定理或推论成立的条件是解决此题的关键.
2.B
【详解】试题分析:如图所示,∠1和∠2两个角都在两被截直线直线b和c同侧,并且在第三条直线a(截线)的两旁,故∠1和∠2是直线b、c被a所截而成的内错角.故选B.
考点:同位角、内错角、同旁内角.
3.B
【分析】根据平移的定义直接判断即可.
【详解】解:由其中一个图形平移得到整个图形的是B,
故选B.
【点睛】此题主要考查了图形的平移,把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,图形的这种移动叫做平移.注意平移是图形整体沿某一直线方向移动.
4.D
【分析】直接根据平行线的判定定理对各选项进行逐一分析即可.
【详解】解:A、∠C=∠1不能判定任何直线平行,故本选项错误;
B、∠A=∠2不能判定任何直线平行,故本选项错误;
C、∠C=∠3不能判定任何直线平行,故本选项错误;
D、∵∠A=∠1,∴EB∥AC,故本选项正确.
故选:D.
【点睛】本题考查的是平行线的判定,用到的知识点为:内错角相等,两直线平行.
5.D
【详解】A、能判断,∵∠1=∠4,∴a∥b,满足内错角相等,两直线平行,不符合题意.
B、能判断,∵∠3=∠5,∴a∥b,满足同位角相等,两直线平行,不符合题意.
C、能判断,∵∠2+∠5=180°,∴a∥b,满足同旁内角互补,两直线平行,不符合题意.
D、不能,符合题意.
故选D.
6.D
【分析】先根据AB∥CD得出∠BCD=∠1,再由CD∥EF得出∠DCE=180°-∠2,再把两式相加即可得出结论.
【详解】解:∵AB∥CD,
∴∠BCD=∠1,
∵CD∥EF,
∴∠DCE=180°-∠2,
∴∠BCE=∠BCD+∠DCE=180°-∠2+∠1.
故选D.
【点睛】本题考查的是平行线的判定,用到的知识点为:两直线平行,内错角相等,同旁内角互补.
7.B
【详解】如图,过点E作EFAB,
∵ABCD,
∴EFABCD,
∴∠1=∠4,∠3=∠5,
∴∠1+∠2+∠3=∠2+∠4+∠5=180°,
故选B.
8.B
【分析】根据平行线的判定定理对各小题进行逐一判断即可.
【详解】解:①∵∠1=∠3,∴l1∥l2,故本小题正确;
②∵∠2+∠4=180°,∴l1∥l2,故本小题正确;
③∵∠4=∠5,∴l1∥l2,故本小题正确;
④∠2=∠3不能判定l1∥l2,故本小题错误;
⑤∵∠6=∠2+∠3,∴l1∥l2,故本小题正确.
故选B.
【点睛】本题考查的是平行线的判定,熟记平行线的判定定理是解答此题的关键.
9.A
【分析】如图,根据平行线的性质可得∠2=∠3,根据三角形外角的性质即可得答案.
【详解】如图,∵长方形的对边平行,
∴∠2=∠3=44°,
∵∠3=∠1+30°,
∴∠1=44°﹣30°=14°.
故选:A.
【点睛】本题考查平行线的性质及三角形外角性质,三角形的一个外角等于与它不相邻的两个内角的和;根据平行线的性质得出∠3的度数是解题关键.
10.A
【分析】先由矩形的性质得出∠BFE=∠DEF=26°,再根据折叠的性质得出∠CFG=180°-2∠BFE,∠CFE=∠CFG-∠EFG即可.
【详解】∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFE=∠DEF=26°,
∴∠CFE=∠CFG-∠EFG=180°-2∠BFE-∠EFG=180°-3×26°=102°,
故选A.
【点睛】本题考查了翻折变换(折叠问题)、矩形的性质、平行线的性质;熟练掌握翻折变换和矩形的性质,弄清各个角之间的关系是解决问题的关键.
11.60°
【分析】利用邻补角定义,再根据∠1与∠2的度数,求出∠AEC的度数,利用内错角相等两直线平行即可得到此时∠C的度数.
【详解】解:∵∠1=70°,∠2=50°,
∴∠AEC=180°-70°-50°=60°,
当∠C=∠AEC=60°时,AB∥CD.
故答案为60°
【点睛】此题考查了平行线的判定,平行线的判定方法有:同位角相等两直线平行;内错角相等两直线平行;同旁内角互补两直线平行,熟练掌握平行线的判定是解本题的关键.
12. ∠1和∠3 ∠2和∠4 ∠5和∠2
【分析】根据内错角的概念,结合图形中各角的位置即可顺利完成填空.
【详解】结合图形可得AB与BC被AD所截得的内错角是∠1和∠3;
DE与AC被直线AD所截得的内错角是∠2和∠4;
因为∠4和∠5是直线AB和AD被直线ED所截构成的内错角,∠4和∠2是直线DE和AC被直线AD所截构成的内错角,
所以图中∠4的内错角是∠5和∠2.
故答案为:∠1和∠3;∠2和∠4;∠5和∠2
【点睛】本题考查了内错角的概念,熟练掌握两个角分别在截线的两侧,且在两条直线之间,具有这样位置关系的一对角叫做内错角是解题的关键.
13.①③④
【分析】根据平行线的判定方法对各小题判断即可解答.
【详解】① ∵,
∴∥(同旁内角互补,两直线平行),正确;
② ∵,
∴∥,错误;
③ ∵,
∴∥(内错角相等,两直线平行),正确;
④ ∵,∴∥(同位角相等,两直线平行),正确;
⑤ 不能证明∥,错误,
故答案为:①③④.
【点睛】本题考查了平行线的判定,熟练掌握平行线的判定方法是解答的关键.
14.130°
【分析】延长AE交与点B,根据平行线的性质求解即可.
【详解】解:如下图,延长AE交与点B,
∵
∴
∵
∴
∴
∴
故答案为:.
【点睛】本题考查的知识点是平行线的判定及性质,熟记判定定理以及性质内容是解此题的关键.
15.20
【分析】由已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,得AB∥DE,过点C作CF∥AB,则CF∥DE,由平行线的性质可得,∠BCF+∠ABC=180°,所以能求出∠BCF,继而求出∠DCF,又由CF∥DE,所以∠CDE=∠DCF.
【详解】解:过点C作CF∥AB,
已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,
∴AB∥DE,
∴CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为:20.
【点睛】此题考查的知识点是平行线的性质,关键是过C点先作AB的平行线,由平行线的性质求解.
16.①②③
【分析】根据垂直定义、角平分线的性质、直角三角形的性质求出∠POE、∠BOF、∠BOD、∠BOE、∠DOF等角的度数,即可对①②③④进行判断.
【详解】①∵AB∥CD,
∴∠BOD=∠ABO=a°,
∴∠COB=180°﹣a°=(180﹣a)°,
又∵OE平分∠BOC,
∴∠BOE=∠COB=(180﹣a)°.故①正确;
②∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=90°﹣(180﹣a)°=a°,
∴∠BOF=∠BOD,
∴OF平分∠BOD.所以②正确;
③∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=a°,
∴∠POE=∠BOF. 所以③正确;
∴∠POB=90°﹣a°,
而∠DOF=a°,所以④错误.
故答案为①②③.
【点睛】本题考查了平行线的性质:两直线平行,内错角相等;解答此题要注意将垂直、平行、角平分线的定义结合应用,弄清图中线段和角的关系,再进行解答.
17.70
【分析】作IF∥AB,GK∥AB,JH∥AB,由题意易得AB∥CD∥ IF∥GK∥JH,则有∠KGF=∠GFI=80°,然后可得∠JHG=∠HGK=70°,进而问题可求解.
【详解】解:作IF∥AB,GK∥AB,JH∥AB,如图所示:
因为AB∥CD,
所以,AB∥CD∥ IF∥GK∥JH,
所以,∠IFE=∠FEC=10°,
所以,∠GFI=90°-∠IFE=80°,
所以,∠KGF=∠GFI=80°,
所以,∠HGK=150°-∠KGF=70°,
所以,∠JHG=∠HGK=70°,
同理,∠2=90°-∠JHG=20°,
所以,∠1=90°-∠2=70°,
故答案为70.
【点睛】本题考查了平行线的性质,正确作出辅助线是关键,注意掌握平行线的性质:两直线平行,内错角相等.
18. AB,BC AC 同旁内角 AB,BC AC 同位角 AB,AC BC 同位角 AC,BC AB 内错角
【详解】试题解析:根据同旁内角、同位角及内错角的概念可得:
(1)∠1和∠3是直线AB、BC被直线AC所截得的同旁内角;
(2)∠1和∠4是直线AB,BC 被直线AC所截得的同位角;
(3)∠B和∠2是直线AB,AC被直线BC所截得的同位角;
(4)∠B和∠4是直线AC,BC被直线AB所截得的内错角.
19.见解析
【分析】由∠1=∠2易得=,由等量代换可得∠3=∠DAC,再根据内错角相等判定.
【详解】∵∠1=∠2(已知)
∴(等式的性质)
即=∠ DAC
∵∠3=∠4,(已知)
∴∠3=∠BAE(等量代换)
∴∠3=∠DAC
∴(内错角相等,两直线平行)
【点睛】本题考查平行线的判定,灵活运用等量代换得到内错角相等是解题的关键.
20.证明见详解.
【分析】由可得,而与互余,所以,所以
,而,所以,所以根据内错角相等两直线平行即可求解;
【详解】
与互余
【点睛】本题主要考查垂直的定义,余角以及平行线的判定,熟练掌握相关定义并准确的进行逻辑推理是求解本题的关键.
21.(1)证明见解析;(2)与∠CED互余的角有∠ADE,∠CDE,∠F,∠FAD.
【分析】(1)依据AB⊥BC于点B,DC⊥BC于点C,即可得到AB∥CF,进而得出∠BAF+∠F=180°,再根据∠BAF=∠EDF,即可得出ED∥AF,依据三角形外角性质以及角平分线的定义,即可得到∠DAF=∠F;(2)结合图形,根据余角的概念,即可得到所有与∠CED互余的角.
【详解】解:(1)∵AB⊥BC于点B,DC⊥BC于点C,
∴∠B+∠C=180°,
∴AB∥CF,
∴∠BAF+∠F=180°,
又∵∠BAF=∠EDF,
∴∠EDF+∠F=180°,
∴ED∥AF,
∴∠ADE=∠DAF,∠EDC=∠F,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DAF=∠F;
(2)∵∠C=90°,
∴∠CED+∠CDE=90°,
∴∠CED与∠CDE互余,
又∵∠ADE=∠DAF=∠EDC=∠F,
∴与∠CED互余的角有∠ADE,∠CDE,∠F,∠FAD.
【点睛】本题主要考查了平行线的判定与性质、余角的概念,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
22.(1)60°;(2)30°;(3)不变.
【分析】(1)由AM∥BN可得∠ABN=180°-∠A,再由BC、BD均为角平分线可求解;
(2)由AM∥BN可得∠ACB=∠CBN,再由∠ACB=∠ABD可得∠ABC =∠DBN;
(3)由AM∥BN可得∠APB=∠PBN,再由BD为角平分线即可解答.
【详解】解:(1)∵AM∥BN,
∴∠ABN=180°﹣∠A=120°,
又∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°,
故答案为60°.
(2)∵AM∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD﹣∠CBD=∠CBN﹣∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=∠ABN=30°,
故答案为30°.
(3)不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=∠PBN=∠APB,即∠APB:∠ADB=2:1.
【点睛】本题考查了平行线的性质.
23.(1);(2),见解析;(3)
【分析】(1)依据AB∥CD,可得∠1=∠EGD,再根据∠2=2∠1,∠FGE=60°,即可得出∠EGD(180°﹣60°)=40°,进而得到∠1=40°;
(2)根据AB∥CD,可得∠AEG+∠CGE=180°,再根据∠FEG+∠EGF=90°,即可得到∠AEF+∠GFC=90°;
(3)根据AB∥CD,可得∠AEF+∠CFE=180°,再根据∠GFE=90°,∠GEF=30°,∠AEG=α,即可得到∠GFC=180°﹣90°﹣30°﹣α=60°﹣α.
【详解】解:(1)∵AB∥CD,
∴∠1=∠EGD.
又∵∠2=2∠1,
∴∠2=2∠EGD.
又∵∠FGE=60°,
∴∠EGD(180°﹣60°)=40°,
∴∠1=40°;
(2)∵AB∥CD,
∴∠AEG+∠CGE=180°,即∠AEF+∠FEG+∠EGF+∠FGC=180°.
又∵∠FEG+∠EGF=90°,
∴;
(3)∵AB∥CD,
∴∠AEF+∠CFE=180°,即∠AEG+∠FEG+∠EFG+∠GFC=180°.
又∵∠GFE=90°,∠GEF=30°,∠AEG=α,
∴∠GFC=180°﹣90°﹣30°﹣α=60°﹣α.
【点睛】本题考查了平行线的性质的运用,解决问题的关键是掌握平行线的性质.
专题01 平行线
注意事项∶
1. 答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上.
2. 所有答案都必须写到答题卷上.选择题必须使用2B铅笔填涂;非选择题必须使用黑色字迹的签字笔或钢笔书写,字体要工整,笔迹要清楚.
3.本试卷分试题卷和答题卷两部分,满分100分.考试时间共90分钟.
一、单选题(共30分)
1.下列说法正确的个数有( )
①同位角相等;②过一点有且只有一条直线与已知直线垂直;③过一点有且只有一条直线与已知直线平行;④若a∥b,b∥c,则a∥c.
A.1个 B.2个 C.3个 D.4个
2.如图,直线a,b被直线c所截,∠1与∠2的位置关系是( )
A.同位角 B.内错角
C.同旁内角 D.对顶角
3.下列图形中,可以由其中一个图形通过平移得到的是( )
A. B. C. D.
4.如图,能判定EB∥AC的条件是( )
A.∠C=∠1 B.∠A=∠2
C.∠C=∠3 D.∠A=∠1
5.如图,下列条件不能判断直线a∥b的是( )
A.∠1=∠4 B.∠3=∠5 C.∠2+∠5=180° D.∠2+∠4=180°
6.如图,若AB∥CD,CD∥EF,那么∠BCE=( )
A.∠1+∠2 B.∠2-∠1
C.180°-∠1+∠2 D.180°-∠2+∠1
7.如图,五边形ABCDE中,ABCD,∠1、∠2、∠3分别是∠BAE、∠AED、∠EDC的外角,则∠1+∠2+∠3等于( )
A.90° B.180° C.210° D.270°
8.如图,下列条件:中能判断直线的有( )
A.5个 B.4个 C.3个 D.2个
9.如图,将一张含有角的三角形纸片的两个顶点叠放在长方形的两条对边上,若,则的大小为( )
A. B. C. D.
10.如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.102° B.108° C.124° D.128°
二、填空题(共21分)
11.如图,∠1=70°,∠2=50°,则∠C= 时,AB∥CD.
12.如图,AB与BC被AD所截得的内错角是 ;DE与AC被直线AD所截得的内错角是 ;图中∠4的内错角是 .
13.如图,给出下列条件:①;②;③;④;⑤.其中,一定能判定∥的条件有 (填写所有正确的序号).
14.如图,直线, .
15.珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,如图,若∠ABC=120°,∠BCD=80°,则∠CDE= 度.
16.如图,AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.有下列结论:①∠BOE=(180-a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确的结论是 (填序号).
17.如图,有两个正方形夹在AB与CD中,且AB∥CD,若∠FEC=10°,两个正方形临边夹角为150°,则∠1的度数为 度(正方形的每个内角为90°)
三、解答题(共49分)
18.看图填空:
(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
19.填写理由:如图,∠1=∠2,∠3=∠4,,试说明.
解:∵∠1=∠2(已知)
∴(______)
即=∠______
∵∠3=∠4,(已知)
∴∠3=∠______(______)
∴∠3=∠______
∴(______)
20.如图,、分别在、上,,与互余,.求证:.
21.如图,AB⊥BC于点B,DC⊥BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF
(1)求证:∠DAF=∠F;
(2)在不添加任何辅助线的情况下,请直接写出所有与∠CED互余的角.
22.如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D,
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.
23.一、问题情境:在综合与实践课上,老师让同学们以“两条平行线AB,CD和一块含角的直角三角尺”为主题开展数学活动.
二、操作发现:
(1)如图1,小明把三角尺的角的顶点G放在CD上,若,求的度数;
(2)如图2,小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上,请你探索并说明与之间的数量关系;
三、结论应用:
(3)如图3,小亮把三角尺的直角顶点F放在CD上,角的顶点E落在AB上.若,求的度数用含的式子表示.
参考答案:
1.A
【分析】根据平行线的性质,垂线的性质和平行公理对各个说法分析判断后即可求解.
【详解】解:①如图,直线AB、CD被直线GH所截,∠AGH与∠CHF是同位角,但它们不相等,故说法错误;
②同一平面内,过一点有且只有一条直线与已知直线垂直,说法错误;
③应为过直线外一点有且只有一条直线与已知直线平行,故说法错误;
④平行于同一直线的两条直线平行,是平行公理的推论,故说法正确.
综上所述,正确的说法是④共1个.
故选A.
【点睛】本题考查了平行线的性质,垂线的性质和平行公理,是基础知识,熟练掌握各定理或推论成立的条件是解决此题的关键.
2.B
【详解】试题分析:如图所示,∠1和∠2两个角都在两被截直线直线b和c同侧,并且在第三条直线a(截线)的两旁,故∠1和∠2是直线b、c被a所截而成的内错角.故选B.
考点:同位角、内错角、同旁内角.
3.B
【分析】根据平移的定义直接判断即可.
【详解】解:由其中一个图形平移得到整个图形的是B,
故选B.
【点睛】此题主要考查了图形的平移,把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同,图形的这种移动叫做平移.注意平移是图形整体沿某一直线方向移动.
4.D
【分析】直接根据平行线的判定定理对各选项进行逐一分析即可.
【详解】解:A、∠C=∠1不能判定任何直线平行,故本选项错误;
B、∠A=∠2不能判定任何直线平行,故本选项错误;
C、∠C=∠3不能判定任何直线平行,故本选项错误;
D、∵∠A=∠1,∴EB∥AC,故本选项正确.
故选:D.
【点睛】本题考查的是平行线的判定,用到的知识点为:内错角相等,两直线平行.
5.D
【详解】A、能判断,∵∠1=∠4,∴a∥b,满足内错角相等,两直线平行,不符合题意.
B、能判断,∵∠3=∠5,∴a∥b,满足同位角相等,两直线平行,不符合题意.
C、能判断,∵∠2+∠5=180°,∴a∥b,满足同旁内角互补,两直线平行,不符合题意.
D、不能,符合题意.
故选D.
6.D
【分析】先根据AB∥CD得出∠BCD=∠1,再由CD∥EF得出∠DCE=180°-∠2,再把两式相加即可得出结论.
【详解】解:∵AB∥CD,
∴∠BCD=∠1,
∵CD∥EF,
∴∠DCE=180°-∠2,
∴∠BCE=∠BCD+∠DCE=180°-∠2+∠1.
故选D.
【点睛】本题考查的是平行线的判定,用到的知识点为:两直线平行,内错角相等,同旁内角互补.
7.B
【详解】如图,过点E作EFAB,
∵ABCD,
∴EFABCD,
∴∠1=∠4,∠3=∠5,
∴∠1+∠2+∠3=∠2+∠4+∠5=180°,
故选B.
8.B
【分析】根据平行线的判定定理对各小题进行逐一判断即可.
【详解】解:①∵∠1=∠3,∴l1∥l2,故本小题正确;
②∵∠2+∠4=180°,∴l1∥l2,故本小题正确;
③∵∠4=∠5,∴l1∥l2,故本小题正确;
④∠2=∠3不能判定l1∥l2,故本小题错误;
⑤∵∠6=∠2+∠3,∴l1∥l2,故本小题正确.
故选B.
【点睛】本题考查的是平行线的判定,熟记平行线的判定定理是解答此题的关键.
9.A
【分析】如图,根据平行线的性质可得∠2=∠3,根据三角形外角的性质即可得答案.
【详解】如图,∵长方形的对边平行,
∴∠2=∠3=44°,
∵∠3=∠1+30°,
∴∠1=44°﹣30°=14°.
故选:A.
【点睛】本题考查平行线的性质及三角形外角性质,三角形的一个外角等于与它不相邻的两个内角的和;根据平行线的性质得出∠3的度数是解题关键.
10.A
【分析】先由矩形的性质得出∠BFE=∠DEF=26°,再根据折叠的性质得出∠CFG=180°-2∠BFE,∠CFE=∠CFG-∠EFG即可.
【详解】∵四边形ABCD是矩形,
∴AD∥BC,
∴∠BFE=∠DEF=26°,
∴∠CFE=∠CFG-∠EFG=180°-2∠BFE-∠EFG=180°-3×26°=102°,
故选A.
【点睛】本题考查了翻折变换(折叠问题)、矩形的性质、平行线的性质;熟练掌握翻折变换和矩形的性质,弄清各个角之间的关系是解决问题的关键.
11.60°
【分析】利用邻补角定义,再根据∠1与∠2的度数,求出∠AEC的度数,利用内错角相等两直线平行即可得到此时∠C的度数.
【详解】解:∵∠1=70°,∠2=50°,
∴∠AEC=180°-70°-50°=60°,
当∠C=∠AEC=60°时,AB∥CD.
故答案为60°
【点睛】此题考查了平行线的判定,平行线的判定方法有:同位角相等两直线平行;内错角相等两直线平行;同旁内角互补两直线平行,熟练掌握平行线的判定是解本题的关键.
12. ∠1和∠3 ∠2和∠4 ∠5和∠2
【分析】根据内错角的概念,结合图形中各角的位置即可顺利完成填空.
【详解】结合图形可得AB与BC被AD所截得的内错角是∠1和∠3;
DE与AC被直线AD所截得的内错角是∠2和∠4;
因为∠4和∠5是直线AB和AD被直线ED所截构成的内错角,∠4和∠2是直线DE和AC被直线AD所截构成的内错角,
所以图中∠4的内错角是∠5和∠2.
故答案为:∠1和∠3;∠2和∠4;∠5和∠2
【点睛】本题考查了内错角的概念,熟练掌握两个角分别在截线的两侧,且在两条直线之间,具有这样位置关系的一对角叫做内错角是解题的关键.
13.①③④
【分析】根据平行线的判定方法对各小题判断即可解答.
【详解】① ∵,
∴∥(同旁内角互补,两直线平行),正确;
② ∵,
∴∥,错误;
③ ∵,
∴∥(内错角相等,两直线平行),正确;
④ ∵,∴∥(同位角相等,两直线平行),正确;
⑤ 不能证明∥,错误,
故答案为:①③④.
【点睛】本题考查了平行线的判定,熟练掌握平行线的判定方法是解答的关键.
14.130°
【分析】延长AE交与点B,根据平行线的性质求解即可.
【详解】解:如下图,延长AE交与点B,
∵
∴
∵
∴
∴
∴
故答案为:.
【点睛】本题考查的知识点是平行线的判定及性质,熟记判定定理以及性质内容是解此题的关键.
15.20
【分析】由已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,得AB∥DE,过点C作CF∥AB,则CF∥DE,由平行线的性质可得,∠BCF+∠ABC=180°,所以能求出∠BCF,继而求出∠DCF,又由CF∥DE,所以∠CDE=∠DCF.
【详解】解:过点C作CF∥AB,
已知珠江流域某江段江水流向经过B、C、D三点拐弯后与原来相同,
∴AB∥DE,
∴CF∥DE,
∴∠BCF+∠ABC=180°,
∴∠BCF=60°,
∴∠DCF=20°,
∴∠CDE=∠DCF=20°.
故答案为:20.
【点睛】此题考查的知识点是平行线的性质,关键是过C点先作AB的平行线,由平行线的性质求解.
16.①②③
【分析】根据垂直定义、角平分线的性质、直角三角形的性质求出∠POE、∠BOF、∠BOD、∠BOE、∠DOF等角的度数,即可对①②③④进行判断.
【详解】①∵AB∥CD,
∴∠BOD=∠ABO=a°,
∴∠COB=180°﹣a°=(180﹣a)°,
又∵OE平分∠BOC,
∴∠BOE=∠COB=(180﹣a)°.故①正确;
②∵OF⊥OE,
∴∠EOF=90°,
∴∠BOF=90°﹣(180﹣a)°=a°,
∴∠BOF=∠BOD,
∴OF平分∠BOD.所以②正确;
③∵OP⊥CD,
∴∠COP=90°,
∴∠POE=90°﹣∠EOC=a°,
∴∠POE=∠BOF. 所以③正确;
∴∠POB=90°﹣a°,
而∠DOF=a°,所以④错误.
故答案为①②③.
【点睛】本题考查了平行线的性质:两直线平行,内错角相等;解答此题要注意将垂直、平行、角平分线的定义结合应用,弄清图中线段和角的关系,再进行解答.
17.70
【分析】作IF∥AB,GK∥AB,JH∥AB,由题意易得AB∥CD∥ IF∥GK∥JH,则有∠KGF=∠GFI=80°,然后可得∠JHG=∠HGK=70°,进而问题可求解.
【详解】解:作IF∥AB,GK∥AB,JH∥AB,如图所示:
因为AB∥CD,
所以,AB∥CD∥ IF∥GK∥JH,
所以,∠IFE=∠FEC=10°,
所以,∠GFI=90°-∠IFE=80°,
所以,∠KGF=∠GFI=80°,
所以,∠HGK=150°-∠KGF=70°,
所以,∠JHG=∠HGK=70°,
同理,∠2=90°-∠JHG=20°,
所以,∠1=90°-∠2=70°,
故答案为70.
【点睛】本题考查了平行线的性质,正确作出辅助线是关键,注意掌握平行线的性质:两直线平行,内错角相等.
18. AB,BC AC 同旁内角 AB,BC AC 同位角 AB,AC BC 同位角 AC,BC AB 内错角
【详解】试题解析:根据同旁内角、同位角及内错角的概念可得:
(1)∠1和∠3是直线AB、BC被直线AC所截得的同旁内角;
(2)∠1和∠4是直线AB,BC 被直线AC所截得的同位角;
(3)∠B和∠2是直线AB,AC被直线BC所截得的同位角;
(4)∠B和∠4是直线AC,BC被直线AB所截得的内错角.
19.见解析
【分析】由∠1=∠2易得=,由等量代换可得∠3=∠DAC,再根据内错角相等判定.
【详解】∵∠1=∠2(已知)
∴(等式的性质)
即=∠ DAC
∵∠3=∠4,(已知)
∴∠3=∠BAE(等量代换)
∴∠3=∠DAC
∴(内错角相等,两直线平行)
【点睛】本题考查平行线的判定,灵活运用等量代换得到内错角相等是解题的关键.
20.证明见详解.
【分析】由可得,而与互余,所以,所以
,而,所以,所以根据内错角相等两直线平行即可求解;
【详解】
与互余
【点睛】本题主要考查垂直的定义,余角以及平行线的判定,熟练掌握相关定义并准确的进行逻辑推理是求解本题的关键.
21.(1)证明见解析;(2)与∠CED互余的角有∠ADE,∠CDE,∠F,∠FAD.
【分析】(1)依据AB⊥BC于点B,DC⊥BC于点C,即可得到AB∥CF,进而得出∠BAF+∠F=180°,再根据∠BAF=∠EDF,即可得出ED∥AF,依据三角形外角性质以及角平分线的定义,即可得到∠DAF=∠F;(2)结合图形,根据余角的概念,即可得到所有与∠CED互余的角.
【详解】解:(1)∵AB⊥BC于点B,DC⊥BC于点C,
∴∠B+∠C=180°,
∴AB∥CF,
∴∠BAF+∠F=180°,
又∵∠BAF=∠EDF,
∴∠EDF+∠F=180°,
∴ED∥AF,
∴∠ADE=∠DAF,∠EDC=∠F,
∵DE平分∠ADC,
∴∠ADE=∠CDE,
∴∠DAF=∠F;
(2)∵∠C=90°,
∴∠CED+∠CDE=90°,
∴∠CED与∠CDE互余,
又∵∠ADE=∠DAF=∠EDC=∠F,
∴与∠CED互余的角有∠ADE,∠CDE,∠F,∠FAD.
【点睛】本题主要考查了平行线的判定与性质、余角的概念,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系.
22.(1)60°;(2)30°;(3)不变.
【分析】(1)由AM∥BN可得∠ABN=180°-∠A,再由BC、BD均为角平分线可求解;
(2)由AM∥BN可得∠ACB=∠CBN,再由∠ACB=∠ABD可得∠ABC =∠DBN;
(3)由AM∥BN可得∠APB=∠PBN,再由BD为角平分线即可解答.
【详解】解:(1)∵AM∥BN,
∴∠ABN=180°﹣∠A=120°,
又∵BC,BD分别平分∠ABP和∠PBN,
∴∠CBD=∠CBP+∠DBP=(∠ABP+∠PBN)=∠ABN=60°,
故答案为60°.
(2)∵AM∥BN,
∴∠ACB=∠CBN,
又∵∠ACB=∠ABD,
∴∠CBN=∠ABD,
∴∠ABC=∠ABD﹣∠CBD=∠CBN﹣∠CBD=∠DBN,
∴∠ABC=∠CBP=∠DBP=∠DBN,
∴∠ABC=∠ABN=30°,
故答案为30°.
(3)不变.理由如下:
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN,
又∵BD平分∠PBN,
∴∠ADB=∠DBN=∠PBN=∠APB,即∠APB:∠ADB=2:1.
【点睛】本题考查了平行线的性质.
23.(1);(2),见解析;(3)
【分析】(1)依据AB∥CD,可得∠1=∠EGD,再根据∠2=2∠1,∠FGE=60°,即可得出∠EGD(180°﹣60°)=40°,进而得到∠1=40°;
(2)根据AB∥CD,可得∠AEG+∠CGE=180°,再根据∠FEG+∠EGF=90°,即可得到∠AEF+∠GFC=90°;
(3)根据AB∥CD,可得∠AEF+∠CFE=180°,再根据∠GFE=90°,∠GEF=30°,∠AEG=α,即可得到∠GFC=180°﹣90°﹣30°﹣α=60°﹣α.
【详解】解:(1)∵AB∥CD,
∴∠1=∠EGD.
又∵∠2=2∠1,
∴∠2=2∠EGD.
又∵∠FGE=60°,
∴∠EGD(180°﹣60°)=40°,
∴∠1=40°;
(2)∵AB∥CD,
∴∠AEG+∠CGE=180°,即∠AEF+∠FEG+∠EGF+∠FGC=180°.
又∵∠FEG+∠EGF=90°,
∴;
(3)∵AB∥CD,
∴∠AEF+∠CFE=180°,即∠AEG+∠FEG+∠EFG+∠GFC=180°.
又∵∠GFE=90°,∠GEF=30°,∠AEG=α,
∴∠GFC=180°﹣90°﹣30°﹣α=60°﹣α.
【点睛】本题考查了平行线的性质的运用,解决问题的关键是掌握平行线的性质.
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
