乘法公式(2)

课件18张PPT。标题 乘法公式(2) 完全平方公式标题a2 ? b2平方差公式 (a+b)(a?b)=练习：
( x + 2y )( x – 2y) = ______
(mn – 3)(mn +3)= ______
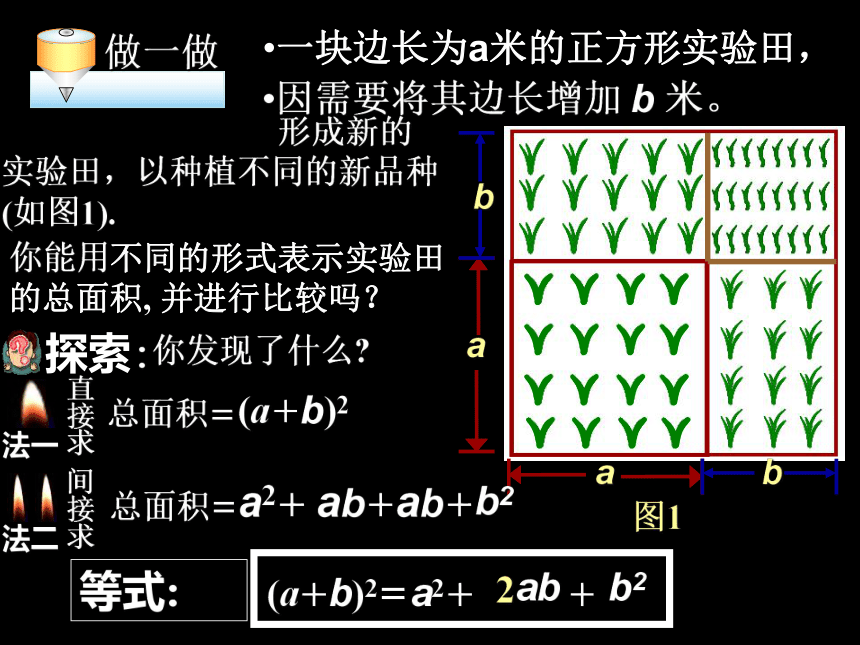
(– 2x+y)(2x+y)= ______x2 –4y2m2n2 –9y2 –4x2多项式的乘法 (a+b)(c+d)acadbcbd=+++图1一块边长为a米的正方形实验田，
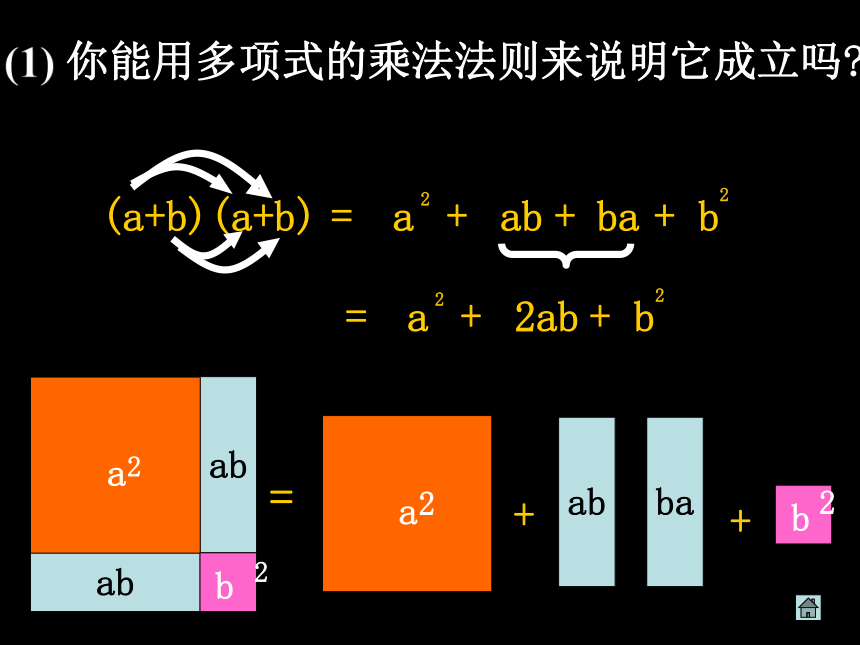
因需要将其边长增加 b 米。 形成新的实验田，以种植不同的新品种(如图1).你能用不同的形式表示实验田的总面积, 并进行比较吗？(a+b)2 a2+ab+ab+b2(a+b)2=a2+ab+b22等式:(a+b)(a+b)abba=+++=abba++(1) 你能用多项式的乘法法则来说明它成立吗?他们是怎么想的?想法对吗？你会如何解决这个问题？利用两数和的
平方
推证= + +＿＿ a22a(?b)(?b)2=a22ab?b2.+(2)有两位同学对两数差的平方有不同的看法:乙:(a?b)2(a+b)2=a2+2ab+b2 ;a2 ?2ab+b2.?= a 2 + 2a(?b) + (?b) 2甲:(a?b)2= a 2?b 2初 识 完全平方公式(a+b)2 = a2+2ab+b2 .
(a?b)2 = a2?2ab+b2 .结构特征:左边是的平方;右边是两数和 (差)两数的平方和加上(减去)这两数乘积的两倍.用自己的语言叙述上面的公式语言表述:两数和 的平方 等于这两数的平方和 加上 这两数乘积的两倍.(差)(减去)注意：
1.完全平方公式和平方差公式的区别！2. (a + b )2≠a2 + b2
(a – b )2 ≠a2 – b2
(a + b ) (a – b ) ﹦ a2 – b222a+ba?ba2 +b2a2 +b2+?2ab2ab( 2x )2 ? 2 ? 2x ? 3 +32
解：(1) (2x?3)2 = 例1 利用完全平方公式计算：
(1) (2x?3)2 ； (2) (4x+5y)2 ; (3) (m n?a)2 先明确用哪个完全平方公式再把计算的式子与完全平方公式对照, 明确哪个是 a , 哪个是 b.4x2=?12x+9 ;（2） （4x + 5y )2= (4x)2 + 2 · 4x · 5y + (5y)2=16 x2 + 40 x y +25y2(3) ( m n ? a )2= ( m n )2 ? 2 · m n · a + a2= m2 n2 ? 2 m n a + a2( a ? b )2= a2 ? 2 a b + b2( 2 x ?3 )2=(2x)2?2·2x· 3+32随堂练习（一） 说出下列各式中的错误，并加以改正：
(1) (2a?1)2＝2a2?2a+1;
(2) (2a+1)2＝4a2 +1；
(3) (?a?1)2＝?a2?2a?1.解: (1)(2a ?1)2＝ (2a)2 ? 2?2a?1 +1=4a2 ?4a +1(2)(2a+1)2＝ (2a)2+2?2a?1 +1=4a2 + 4a +1
(3)(?a?1)2＝(?a)2?2? ( ?a) ?1 + 1=a2 + 2a + 1 (二) (1) ( x + 2y)2 ； (2) ( n – 3m)2 ; (3) (2xy – Z)2 ;2、计算：1. 填空:(1) ( 2x + y)2 = 4x2 + ( ____________ ) + y2
(2) (x ? ______)2 = x2 – (_________) + 25y2
(3) (_____ ? b )2 = 9 a2 ?(__________) + (____)2
(4) x 2 + x +(_______) = ( x +_____)24 x y5 y10 x y3 ab6 a b0.50.25例题例2：利用完全平方公式计算：
(1) 0.982 (2) 10012解：(1) 原式 = （ 1 ? 0.02）2= 12 ? 2 ×1×0.02 + 0.022= 1 ? 0.04 + 0.0004= 0.9604（2）原式 = （ 1000 + 1 ）2= 10002 + 2 × 1000×1 + 12= 1000000 + 2000 + 1=1002001
类似地,当a=30,a=27时, 3a+2.25的值分别为92.25,83.25.所以4块花苗圃 的面积分别增加了92.55m2,90.75m2,92.25m2,83.25m2.例3 一花农有4块正方形花苗圃,边长分别为30.1m ,29.5m,30m,27m.现将这4块苗圃的边长都增加1.5m后,求各苗圃的面积分别增加了多少m2?设原正方形苗圃的边长为a m,边长增加
(a+1.5) m则: (a+1.5)2-a2=a2+3a+2.25-a2=3a+2.25当a=30.1时,3a+2.25=3×30.1+2.25=92.55当a=29.5时,3a+2.25=3×29.5+2.25=90.751.5 m后,新正方形的边长为本节课你学到了什么?注意完全平方公式和平方差公式不同： 完全平方公式的结果 是三项，即
(a ± b)2＝a2 ± 2ab + b2. 平方差公式的结果 是两项，即
(a+b)(a?b)＝a2?b2. 有时需要进行变形，使变形后的式子符合应
用完全平方公式的条件，即为“两数和(或差)
的平方”，然后应用公式计算. 在解题过程中要准确确定a和b、对照公式原形的两边, 做到不丢项、不弄错符号、2ab时不少乘2.知识小园地利用杨辉三角对完全平方公式进行推广（a+b)0=1(a+b)1=a+b(a+b)2=a2+2ab+b2(a+b)3=a3+3a2b+3ab2+b3(a+b)4=a4+4a3b+6a2b2+4ab3+b4? 贾宪最著名的数学成就，是他创制了一幅数字图式，即“开方作法本源图”。这幅图现见于杨辉的书中，但杨辉在引用了这幅图后特意说明：“贾宪用此术”。所以过去我国数学界把这幅图称为“杨辉三角”，实际上是不妥当的，应该称为“贾宪三角”才最为恰当。
?? 由于史书没有贾宪的传记，所以我们今天对这位数学家的生平事迹已经无法搞清楚了。只知道他曾经当过宋代”左班殿直”的小官，是当时天文数学家楚衍的学生，还写过两部数学著作，可惜这两部著作现在都失传了。幸亏南宋数学家杨辉在他的书中引述了贾宪的许多数学思想资料，才使我们今天得以了解贾宪在数学上的重大贡献。 知识小园地（贾宪三角）小组抢答 1. 下列等式是否成立? 说明理由．
(1) (?4a+1)2=(1?4a)2；
(2) (?4a?1)2=(4a+1)2；
(3) (4a?1)(1?4a)＝(4a?1)(4a?1)＝(4a?1)2；
(4) (4a?1)(?1?4a)＝(4a?1)(4a+1).(1) 由加法交换律 ?4a+l＝l?4a。成立理由:(2) ∵ ?4a?1＝?(4a+1)，成立∴(?4a?1)2＝[?(4a+1)]2＝(4a+1)2.(3) ∵ (1?4a)＝?(?1+4a)不成立．即 (1?4a)＝?(4a?1)＝?(4a?1)，∴ (4a?1)(1?4a)＝(4a?1)·[?(4a?1)]＝?(4a?1)(4a?1)＝?(4a?1)2。 不成立．(4) 右边应改为: ?(4a?1)(4a+1)。a2ababb2(a+b)2 =a?ba?bb(a?b)(a?b)2a2+2ab+b2即 (a?b)2 = a2?2ab+b2(a?b)2 = a2? ab ? b(a?b)　　　　　　试一试
　你能由两数和的完全平方公式的几何意义推想到两数差的完全平方公式的几何意义吗？拓 展 练 习1.思考：试一试：计算 ( m ?2n + 3 )2 2.完全平方公式的变形应用：(1) 已知：x +y =3 ; x y =2 求 x2+y2 ； (x ?y)2 的值(2)已知：a ?b =1 ； a2 +b2 =25 求 ab 的值(3)已知：(x +y )2 =9 ; ( x ? y)2= 5 求 xy ; x2+y2 的值作业 作业1、基础练习：见作业本
2、知识拓展：课本p130第2 、 4 、5 题。