提取公因式法

课件18张PPT。6.2 提取公因式法你能把12、15因数分解吗？12=2 × 2×3；
15= 3 × 512、15这两数有公因数吗？多项式中ma+mb有公共的因式吗？如果有，请你指出来！联想和类比一下！? a c+ b c
?3 x2 +x
?30 m b2 + 5n b
?3x+6
? a2 b – 2a b2 + ab
? 7 ( a– 3 ) – b ( a– 3)
下列各多项式中的各项有没有共同的因式？c x5b3ab
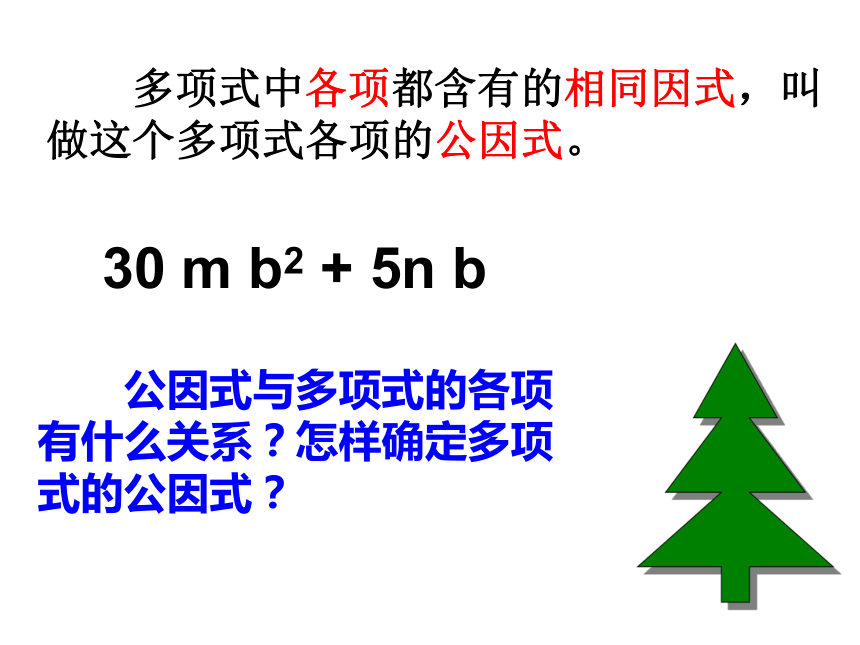
a-3试一试你的眼光！ 多项式中各项都含有的相同因式，叫做这个多项式各项的公因式。 公因式与多项式的各项有什么关系？怎样确定多项式的公因式？30 m b2 + 5n b 正确找出多项式各项公因式的关键是什么？系数：1、公因式的系数是多项式各项系数 的最大公约数。 字母： 2、字母取多项式各项中都含有的相同的字母。
指数： 3、相同字母的指数取各项中最小的一个，即字母最低次幂.
4、多项式中的公因式可以是单项式，
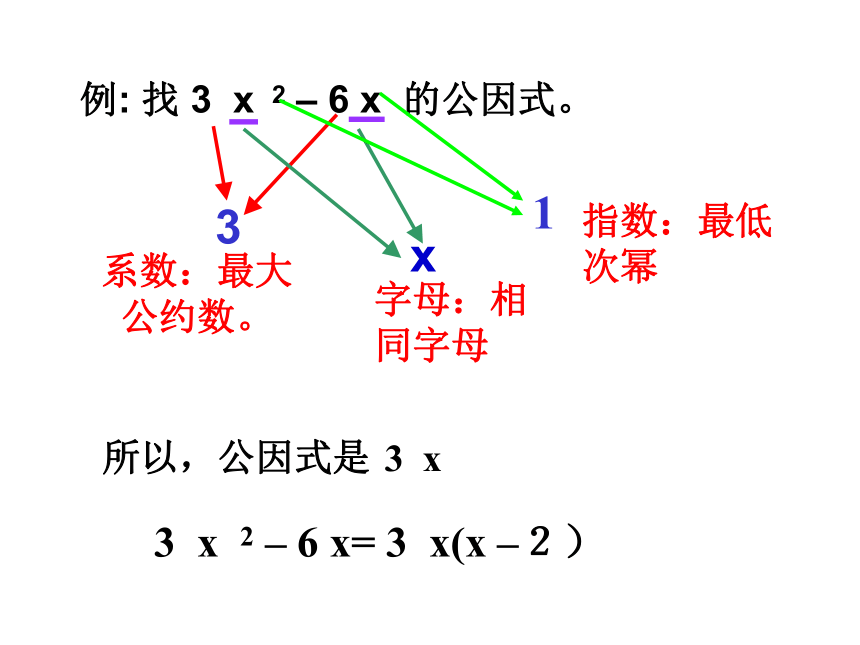
也可以是多项式。例: 找 3 x 2 – 6 x 的公因式。系数：最大
公约数。3字母：相同字母
x 所以，公因式是指数：最低次幂13 x3 x 2 – 6 x= 3 x(x –２）提取公因式法分解因式
如果一个多项式的各项含有公因式，那么就可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提取公
因式法。指出下列多项式中各项的公因式：（1） （2） （3） （4）? 7x2 – 21x ?8 a 3 b2 –12ab 3 + ab
? m b2 + n b ?7x 3y2 –42x2y 3
? a2 b – 2a b2 + abc
? 7 ( x – 3 ) – x ( 3 – x )
⑦—4x2+8ax+2x
⑧—3ab+6abx—9abx 把下列各式分解因式。
当首项的系数为负时,通常应提取负因数,此时剩下的各项都改变符号.（1）2x2 + 3x3 + x = x(2x +3x2)（2）3a2c - 6a3c = 3a2(c - 2ac)（3）-2s3 + 4s2 - 6s = - s(2s2 + 4s - 6)（4）-4a2b + 6ab2 - 8a = -2ab(2a-3b) - 8a下列的分解因式对吗？如不对，请指出原因:应为: 原式=x(2x +3x2+1)应为: 原式=-2s(s2-2s+3)应为: 原式= -2a (2ab-3b2+4)应为: 原式=3a2c(1 -2a)①提取不尽③疏忽变号④只提取部分公因式,整个式子未成乘积形式。(3).提取公因式的一般步骤:①确定应提取的公因式:②用公因式去除这个多项式,把所得的商作为另一个因式:③把多项式写成这两个因式的积的形式。【反思】(2).提取公因式要彻底;注意易犯的错误:②漏项(1).当首项系数为负时,通常应提取负因数,在提取“－”号时,余下的各项都变号。下面的解法对吗？
把 8 a 3 b2 –12ab 3 c + ab分解因式.解：8 a 3 b2 –12ab 3 c + ab
=ab(8a2 b- 12 b2 c)当多项式的某一项和公因式相同时，提取公因式后剩余的项是1。=ab?8a2 b-ab ? 12 b2 c+ab ? 1解：问：（a-b)2 - (b-a)3能因式分解吗？原式=2(a-b)2-(a-b)=(a-b)〔 2(a-b)-1 〕=(a-b)(2a-2b-1)原式=(a-b)2+(a-b)3=(a-b)2(a-b+1)或者原式=(b-a)2-(b-a)3=(b-a)2〔1-(b-a)〕=(b-a)2(1-b+a)把2(a—b)2—a+b 分解因式.做一做:在下列各式等号右边填入“+”或“-”号,使等式成立:————+ + 归纳 括号前面是“+”号,括到括号里的各项都不变号;括号前面是“—”号,括到括号里的各项都变号.? 25x-5
? 3 x3 -3x2 –9x
? 8a 2c+ 2b c
? -4a 3b3 +6 a2 b-2ab
? a(x-y)+by-bx 把下列各式分解因式：
=5(5x-1)=3x(x2-x-3)=2c(4a2+b)=-2ab(2a2b2-3a+1)= (x-y)(a-b) 练一练 =a(x-y)+b(y-x)=a(x-y)-b(x-y)综合练习：1、分解因式计算（-2）101+（-2）100
2、利用简便方法计算：
4.3x199.8+0.76x1998-1.9x199.8
3、已知a+b=3,ab=2,求代数式
a2 b + 2 a2 b2 +a b2的值.
4、把 9am+1 –21 am+7a m-1分解因式.1、确定公因式的方法：
(1)公因式的系数是多项式各项系数的最大公约数。
(2)字母取多项式各项中都含有的相同的字母。
(3)相同字母的指数取各项中最小的一个，即最
低次幂
小结2、提公因式法分解因式：
两步：第一步，找出公因式；第二步，提公因式 ，即用多 项式除以公因式.