1.4平行线的性质(1)课件

(共20张PPT)
1.4平行线的性质(1)
1、判断两直线平行的方法有哪几种？
同位角相等，两直线平行。
内错角相等，两直线平行。
同旁内角互补，两直线平行。
这些判定方法的条件是什么，结果是什么？
角
线
b
1
2
3
4
5
6
7
8
a
c
条件 结论
∠1=∠5 ∠2=∠6
∠3=∠7 ∠4=∠8
∠3=∠6 ∠4=∠5
∠4+∠6=180°
∠3+∠5=180°
a∥b
内错角相等
同旁内角互补
同位角相等
知识回顾
如图：怎样判断直线a∥b
两直线平行，
阅读课本14—15页的内容，完成下列问题。
任意画两条互相平行的直线,再任意画一条直线与这两条平行线相交.测量同位角的度数,你发现了什么 与其他同学的发现相同吗
平行线的性质:_______________________________________
　　　　　　
　几何语言：　_______________　　________________　
实 验
（1）已知a//b，任意画一条直线c与平行线a、b相交。
（2）任选一对同位角，用适当
的 方法实验，看看这一对同位角有什么关系
65°
65°
c
a
b
1
5
2
3
4
6
7
8
∠1=∠5
a∥b
方法一：度量法
1
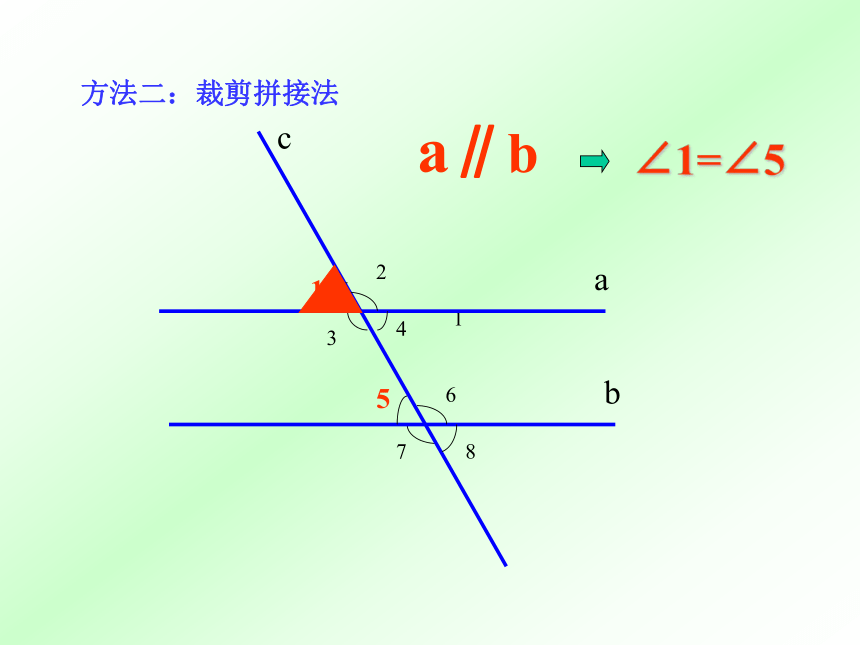
方法二：裁剪拼接法
b
5
6
8
a
c
2
3
4
7
1
∠1=∠5
a∥b
c
a
b
1
5
2
3
4
6
7
8
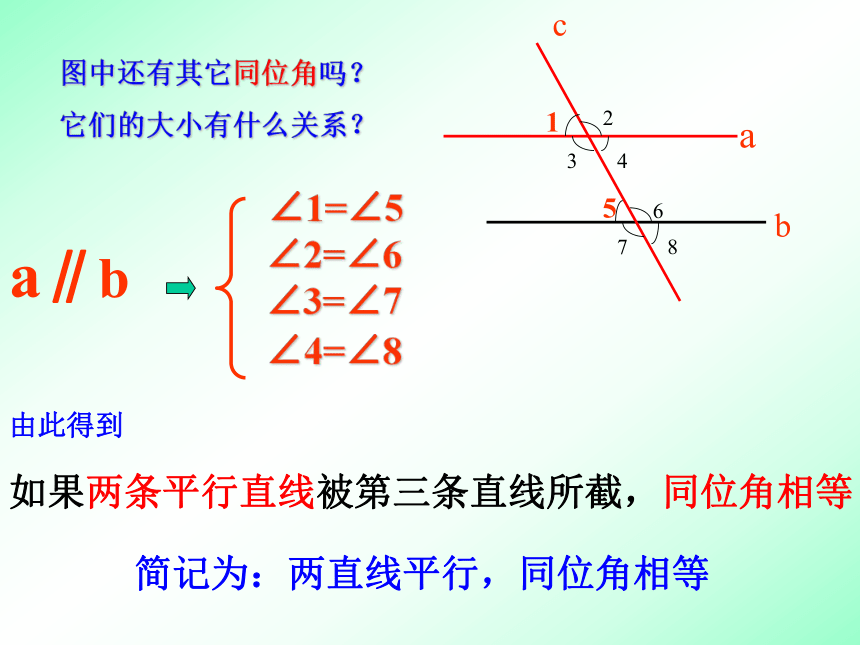
图中还有其它同位角吗？
它们的大小有什么关系？
简记为：两直线平行，同位角相等
∠1=∠5
∠2=∠6
∠3=∠7
∠4=∠8
a∥b
如果两条平行直线被第三条直线所截，同位角相等
由此得到
c
a
b
1
2
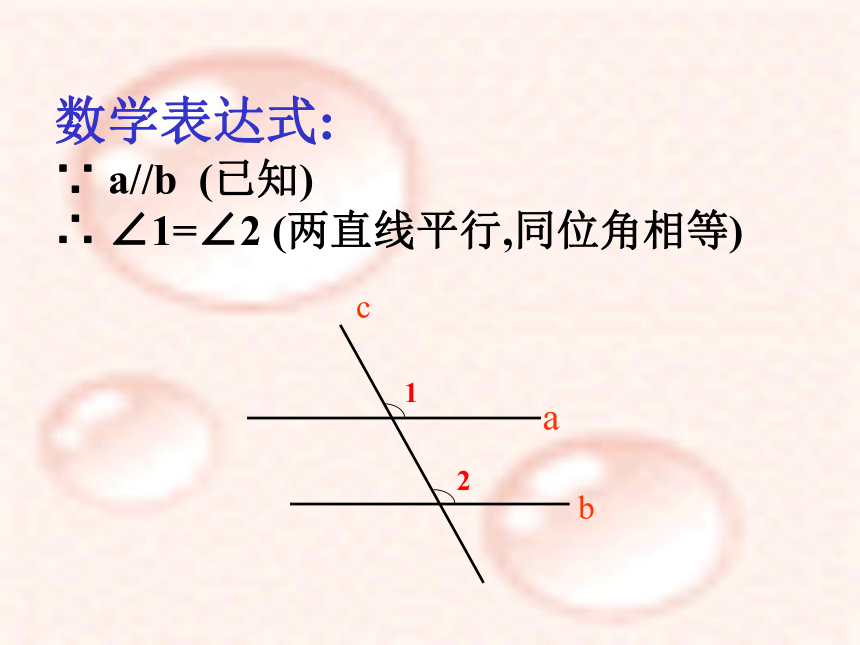
数学表达式:
∵ a//b (已知)
∴ ∠1=∠2 (两直线平行,同位角相等)
b
a
1
c
问题: (1) 凡是同位角相等这句话对吗
(2) 两直线被第三条直线所截,同位角相等吗
(3) 两条直线在什么情况下, 同位角会相等呢
2
b
1
2
3
4
5
6
7
8
a
c
性质和判定的比较
两条直线被第三条直线直线所截
同位角相等，
两直线平行，
判定
性质
条件 结论
条件 结论
思考:
1、判定与性质的条件与结论有什么关系？
互换
2、使用判定时是
已知 说明 ；
角的相等
两直线平行
使用性质时是
已知_____________说明___________。
两直线平行
角的相等
两直线平行。
同位角相等。
三、随堂练习
如图所示，a∥b,c∥d。
找出与∠1相等的角。
如图，与∠1相等的角有：
∠3， ∠5， ∠7， ∠9，∠11， ∠13， ∠15；
解：
1
14
16
13
15
3
2
4
5
6
7
8
9
10
12
11
找一找!
a
b
c
d
例1、如图，梯子的各条横档互相平行，∠1=1050，求∠2的度数。
A
B
C
D
1
2
3
1、如图：已知直线l3∥l2 ，
∠1＝40o，求∠2的度数。
1
2
课内练习1：
40°
2、课文P16作业题T1.
例2、如图，已知∠1=∠2，若直线a⊥m，则直线b⊥m，请说明理由.
1
2
3
4
n
m
a
b
3、已知a，b，c，d四条直线如图。
（1）图中哪些直线互相平行 哪些直线相交
（2）说出∠α的度数。
a
b
c
d
76o
77o
76o
α
a//b
77°
课内练习2：
4、课文P16作业题T2，T4
小 结
判 定
性 质
由“线”定“角”
由“线”的位置关系（平行），定“角”的数量关系（相等）
由“角”定“线”
由“角”的数量关系（相等），定“线”的位置关系（平行）
拓展提高
1、如图，若AB∥CD，且∠1 =∠2，，试判断AM与CN的位置关系，并说明理由。
2、课文P16 T5
布置作业
1、作业本（1）
2、预习课文P7——18