运用乘法公式分解因式2(浙江省杭州市西湖区)
文档属性
| 名称 | 运用乘法公式分解因式2(浙江省杭州市西湖区) |

|
|
| 格式 | rar | ||
| 文件大小 | 558.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-06-11 10:40:00 | ||
图片预览








文档简介
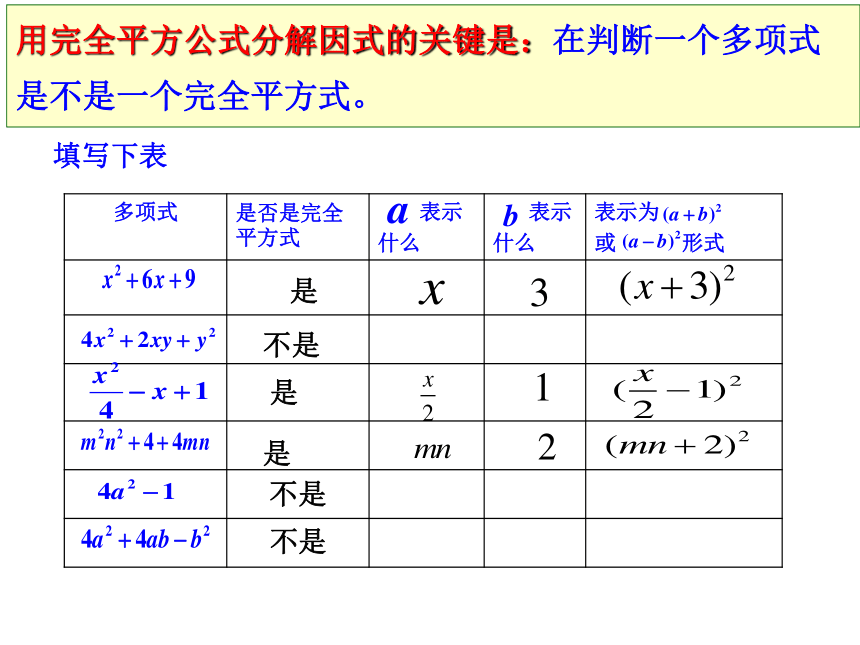
课件21张PPT。试一试你知道这四个图形的面积和是多少吗?你能把这四个图形拼成一个大正方形吗?如果能,那么正方形的边长是多少?面积是多少?你能用等式来表示这一变化吗?=完全平方公式公式逆用:很显然,我们可以运用以上这个公式来分解因式了,我们把它称为“完全平方公式”用完全平方公式分解因式我们把以上两个式子叫做完全平方式判别下列各式是不是完全平方式是是是是完全平方式的特点:1、必须是三项式2、有“a” 、“b”的平方 3、有 “a” 、“b”的2倍或-2倍A2±2×A×B+B2请补上一项,使下列多项式成为完全平方式(±2xy)(±4xy)(±ab)(±12ab)用完全平方公式分解因式的关键是什么?用完全平方公式分解因式的关键是:在判断一个多项式是不是一个完全平方式。填写下表是不是是是不是不是例题:把下列式子分解因式4x2+12xy+9y2A2±2×A×B+B2=(A±B)2例1:把下列各式分解因式把下列各式分解因式:考考你看谁算的最快:例2:因式分解整体思想换元思想 学以致用
多项式:
(x+y)2-2(x2-y2)+(x-y)2
能用完全平方公式分解吗?已知 a、b、c为三角形的三边,试判断
a2 -2ab+b2-c2大于零?小于零?等于零?解: a2 -2ab+b2-c2
=(a-b)2 -c2 因此 a2 -2ab+b2-c2小于零。即:(a-b+c)(a-b-c) ﹤0∴ a-b+c﹥0 a-b-c ﹤0∴ a+c ﹥b a﹤b+c∵ a、b、c为三角形的三边 =(a-b+c)(a-b-c)挑战自我
1、将 再加上一项,使它成为完全平方式,你有几种方法?
2、在括号内补上一项,使多项式成为完全平方式:X4+4x2+( )
练习题:1、下列各式中,能用完全平方公式分解的是( )
A、a2+b2+ab B、a2+2ab-b2
C、a2-ab+2b2 D、-2ab+a2+b2
2、下列各式中,不能用完全平方公式分解的是( )
A、x2+y2-2xy B、x2+4xy+4y2
C、a2-ab+b2 D、-2ab+a2+b2
DC5、把 分解因式得
( )
A、 B、
6、把 分解因式得
( )
A、 B、BA7、如果100x2+kxy+y2可以分解为(10x-y)2,那么k的值是( )
A、20 B、-20
C、10 D、-10
8、如果x2+mxy+9y2是一个完全平方式,那么m的值为( )
A、6 B、±6
C、3 D、±3 BB9、把 分解因式得( )
A、 B、
C、 D、
10、计算 的结果是( )
A、 1 B、-1
C、 2 D、-2CA小结:1、是一个二次三项式2、有 “a” 、“b”的平方,而且有“a” 、“b” 的积的两倍或负两倍3、我们可以利用完全平方公式来进行因式分解完全平方式具有:
多项式:
(x+y)2-2(x2-y2)+(x-y)2
能用完全平方公式分解吗?已知 a、b、c为三角形的三边,试判断
a2 -2ab+b2-c2大于零?小于零?等于零?解: a2 -2ab+b2-c2
=(a-b)2 -c2 因此 a2 -2ab+b2-c2小于零。即:(a-b+c)(a-b-c) ﹤0∴ a-b+c﹥0 a-b-c ﹤0∴ a+c ﹥b a﹤b+c∵ a、b、c为三角形的三边 =(a-b+c)(a-b-c)挑战自我
1、将 再加上一项,使它成为完全平方式,你有几种方法?
2、在括号内补上一项,使多项式成为完全平方式:X4+4x2+( )
练习题:1、下列各式中,能用完全平方公式分解的是( )
A、a2+b2+ab B、a2+2ab-b2
C、a2-ab+2b2 D、-2ab+a2+b2
2、下列各式中,不能用完全平方公式分解的是( )
A、x2+y2-2xy B、x2+4xy+4y2
C、a2-ab+b2 D、-2ab+a2+b2
DC5、把 分解因式得
( )
A、 B、
6、把 分解因式得
( )
A、 B、BA7、如果100x2+kxy+y2可以分解为(10x-y)2,那么k的值是( )
A、20 B、-20
C、10 D、-10
8、如果x2+mxy+9y2是一个完全平方式,那么m的值为( )
A、6 B、±6
C、3 D、±3 BB9、把 分解因式得( )
A、 B、
C、 D、
10、计算 的结果是( )
A、 1 B、-1
C、 2 D、-2CA小结:1、是一个二次三项式2、有 “a” 、“b”的平方,而且有“a” 、“b” 的积的两倍或负两倍3、我们可以利用完全平方公式来进行因式分解完全平方式具有:
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
