分式复习课(浙江省温州市苍南县)

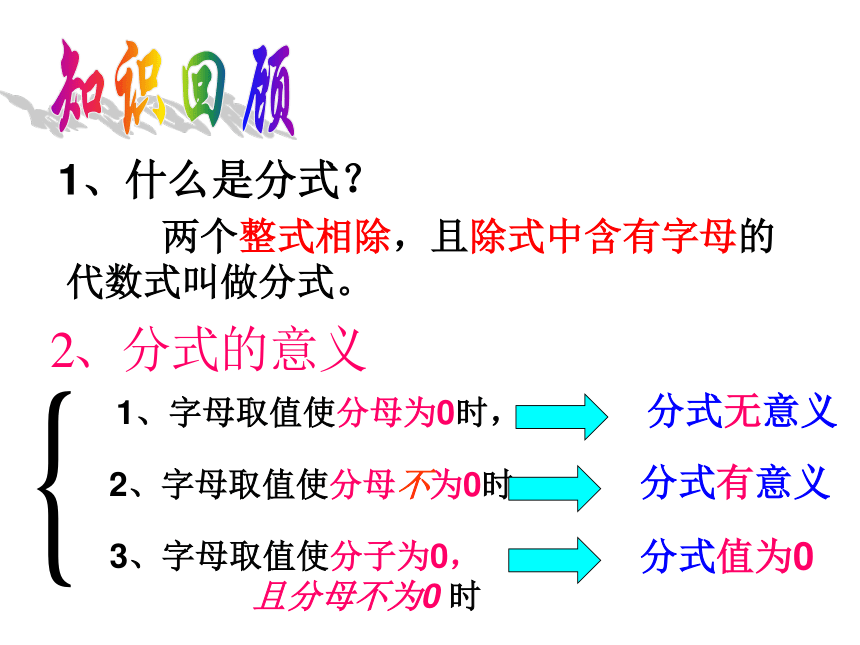
课件19张PPT。第七章 分式复习分式的概念、性质分式方程及其应用分式的乘除、加减 两个整式相除，且除式中含有字母的代数式叫做分式。知识回顾1、什么是分式？1、字母取值使分母为0时，分式无意义2、字母取值使分母不为0时，分式有意义3、字母取值使分子为0，
且分母不为0 时分式值为0辨一辨下列代数式中，哪些是整式？哪些是分式？整式有:分式有:练一练x≠3X=3-4填空:
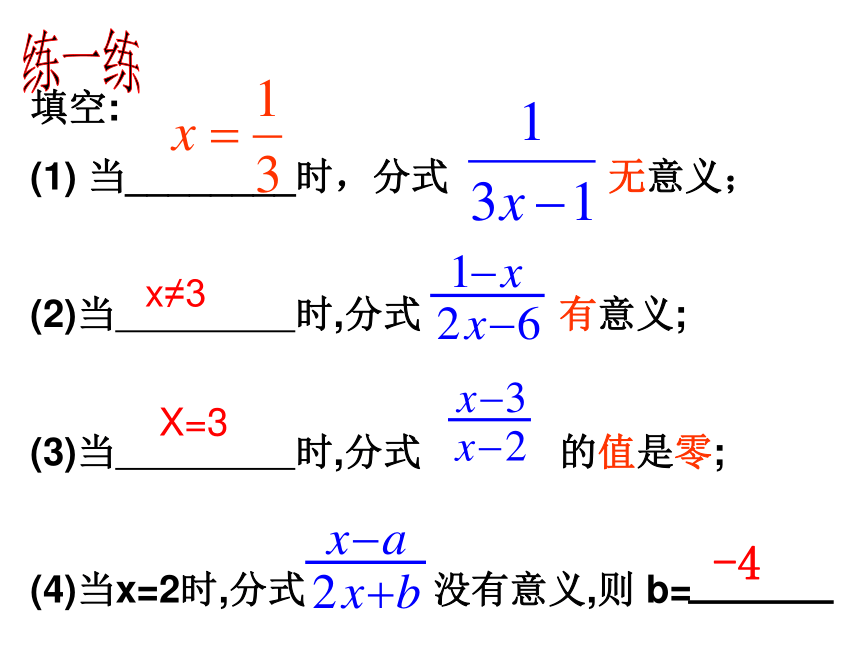
(1) 当________时，分式 无意义；
(2)当 时,分式 有意义;
(3)当 时,分式 的值是零;
(4)当x=2时,分式 没有意义,则 b= (5) 已知分式当 时,分式有意义;
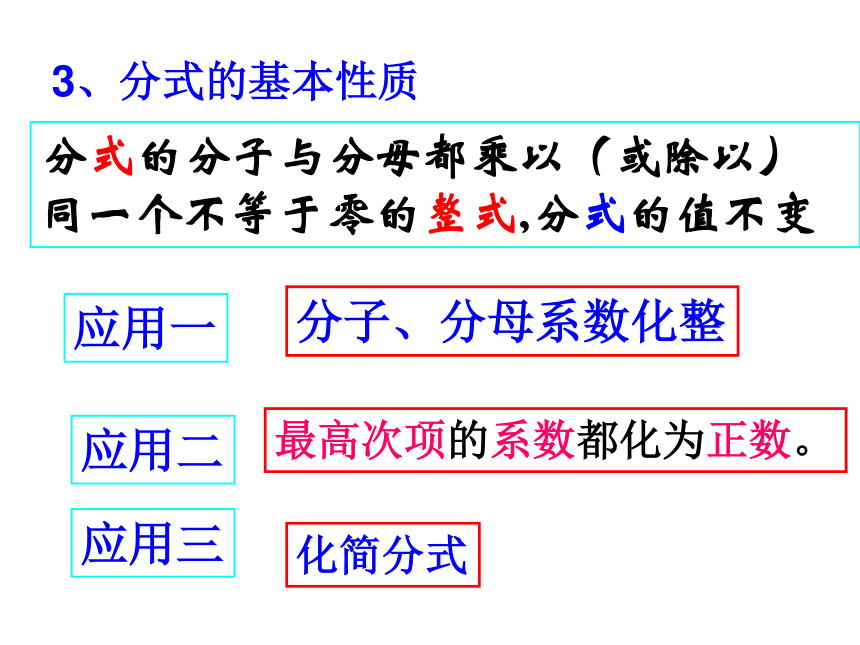
当 时,分式的值是零;练一练D3、分式的基本性质分式的分子与分母都乘以（或除以） 同一个不等于零的整式,分式的值不变应用一分子、分母系数化整应用二最高次项的系数都化为正数。应用三化简分式分式性质应用１：不改变分式的值，把下列各式的分子与分母中各项的系数都化为整数：不改变分式的值，把下列分式的分子
与分母的最高次项的系数都化为正数。分式性质应用2：化简下列分式：分式性质应用3：4、分式乘除法的法则计
算5、（1）同分母分式的加减法法则：计
算:5、（2）异分母分式的加减法法则：步骤：1、找公分母；2、通分；
3、转化为同分母加减的法则计算并化简计算先化简，再求值：6、分式方程：方程中只含分式,或分式和整式,且分母含有未知数的方程.1、下列方程中，是分式方程（ ）C验 根关键：找公分母注意：不要漏乘某人骑自行车比步行每小时多走8千米， 如果他步行12千米所用时间与骑车行36千米所用的时间相等，求他步行的速度是多少千米/小时？
解:设他步行的速度是x千米/小时，根据题意列方程一、列分式方程解决实际问题公式的变形
2、下列分式是最简分式的是 ( )
(A) (B) (C) (D)
CC１.下列变形正确的是 ( )
A B

C D3、如果把分式 中的 和 都扩大5倍，
那么这个分式的值 （ ）
A.扩大为原来的5倍 B. 不变
C.缩小到原来的 D.扩大到原来的25倍 xy选一选BA作业：作业纸第七章复习题