分式期末复习

课件29张PPT。分式期末复习基础回顾：(1)根据规律可知第5个数应是 ,(2)可知第n个数应是 (n为正整数)分式的特征:①表示两个整式相除，
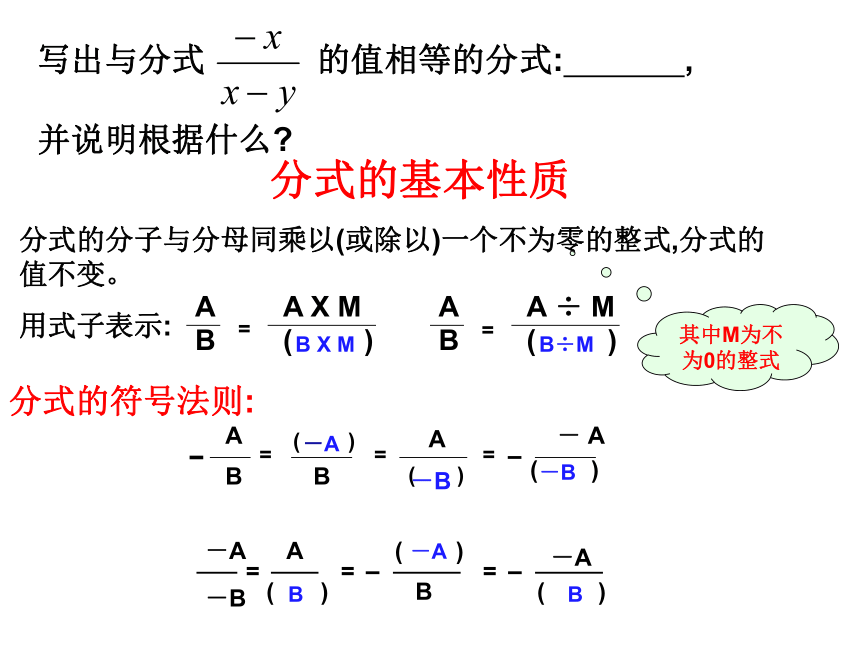
　　　 　　②除式中要含有字母．1.分式的定义:2.分式有意义的条件:B≠0分式无意义的条件:B = 03.分式值为 0 的条件:A=0且 B ≠0分式的概念基础回顾：①③④⑤⑥⑧ 分式的基本性质
分式的分子与分母同乘以(或除以)一个不为零的整式,分式的值不变。
用式子表示: B X MB÷M－A－B－BB－AB其中M为不为0的整式0,2,-2,-4分式的乘除法法则分式的加减32x=2 x≠3且x ≠-3填一填a2+ab1CCxyBA选一选 4、要使分式 有意义，则x的取值范围是

A、 B、
C、 且 D、 或
5、下列等式成立的是 （ ）
A. B.

C. D.
6、下列各分式中，与 分式的值相等的是（ ）
A. B. C. D.
CDCCC练一练77解:∴ A+1=0, ∴ A=－1212311做一做解（1）原式=（2）原式算一算综合与拓展经检验：分式方程必须检验,若有增根,要舍去找出公分母例2、丽园”开发公司生产的960件新产品，需要精加工后，才能投放市场。现有甲、乙两个工厂都想加工这批产品，已知甲工厂单独加工完这批产品比乙工厂单独加工完这批产品多用20天，而乙工厂每天比甲工厂多加工8件产品，公司需付甲工厂加工费用每天80元，乙工厂加工费用每天120元。
（1）求甲、乙两个工厂每天各能加工多少件新产品。 请你帮助公司选择一种既省时又省钱的加工方案，并说明理由。 （2）公司制定产品加工方案如下：可以由每个厂家单独完成；也可以由两个厂家同时合作完成。在加工过程中，公司需派一名工程师每天到厂进行技术指导，并负担每天5元的误餐补助费。解：（1）设甲工厂每天能加工x件产品，则乙工厂每天能加工(x+8)件产品。根据题意，得： 整理得:x2+8x-384=0, x1=16,x2=-24.
经检验:x1=16,x2=-24都是原方程的根。但是每天能加工的产品数不能为负数，
∴x=-24舍去，只取x=16.当x=16时，x+8=24. 答：甲、乙两个工厂每天各能加工16件和24件新产品。（2）甲工厂单独加工完这批新产品所需的时间为：
　　　　　　960÷16=60（天）
所需要费用为：80×60＋5×60＝5100（元）
　　乙工厂单独加工完这批新产品所需的时间为：
　　　　　960÷24＝40（天）
　 所需要费用为： 120×40＋5×40＝5000（元） 　　设他们合作完成这批新产品所用的时间为y天，于是因为甲乙两家工厂合作所用时间和钱数都最少，所以 选择甲乙两家工厂合作加工完这批新残品比较合适。 解得：y=24（天）所需费用为：(80+120) ×24 +5 × 24=4920（元） 1、某校组织学生360名师生去参观某公园，如果租用甲种客车客车刚好坐满；如果租用乙种客车可少用一
辆，且余40个空座位.
(1)已知甲种客车比乙种客车少20个座位,求甲、乙两种客车各有多少个座位。
（2）已知甲种客车的租金每辆400元，乙种客车的租金每辆480元。这次参观同时租用这两种客车，其中甲种客车比乙种客车少祖一辆，所用租金比单独租用任何一种客车要节省， 按这种方案需用租金多少元？练一练解：设甲种每辆客车有 x个座位，则乙种客车每辆有(x+20)个座位，根据题意，可列方程：解得:x1=60,x2=-120.经检验：x1=60,x2=-120都是原方程的根.
但x2=-120不合题意舍去,只取x=60,这时x+20=80.答:甲乙两种客车的作为分别有个个座位。 2、通常购买同一品种的西瓜时,西瓜的质量越大,花费的钱越多. 因此人们希望西瓜瓤占整个西瓜的比例越大越好. 假如我们把西瓜都看成球形,并把西瓜瓤的密度看成是均匀的, 西瓜的皮厚都是d .(1) 西瓜瓤与西瓜的体积各是多少?(1) 西瓜瓤与西瓜的体积各是多少?
(2) 西瓜瓤与西瓜的体积的比是多少?
(3) 买大西瓜合算还是买小西瓜合算?西瓜的皮厚都是d .解：设西瓜的半径为R , 小大大再见