2024浙教版数学七年级下册--第1章《平行线》素养综合检测卷(含解析)
文档属性
| 名称 | 2024浙教版数学七年级下册--第1章《平行线》素养综合检测卷(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 508.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 08:49:51 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024浙教版数学七年级下册
第1章·素养综合检测卷
(考查范围:平行线 时间:60分钟 满分:100分)
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题3分,共24分)
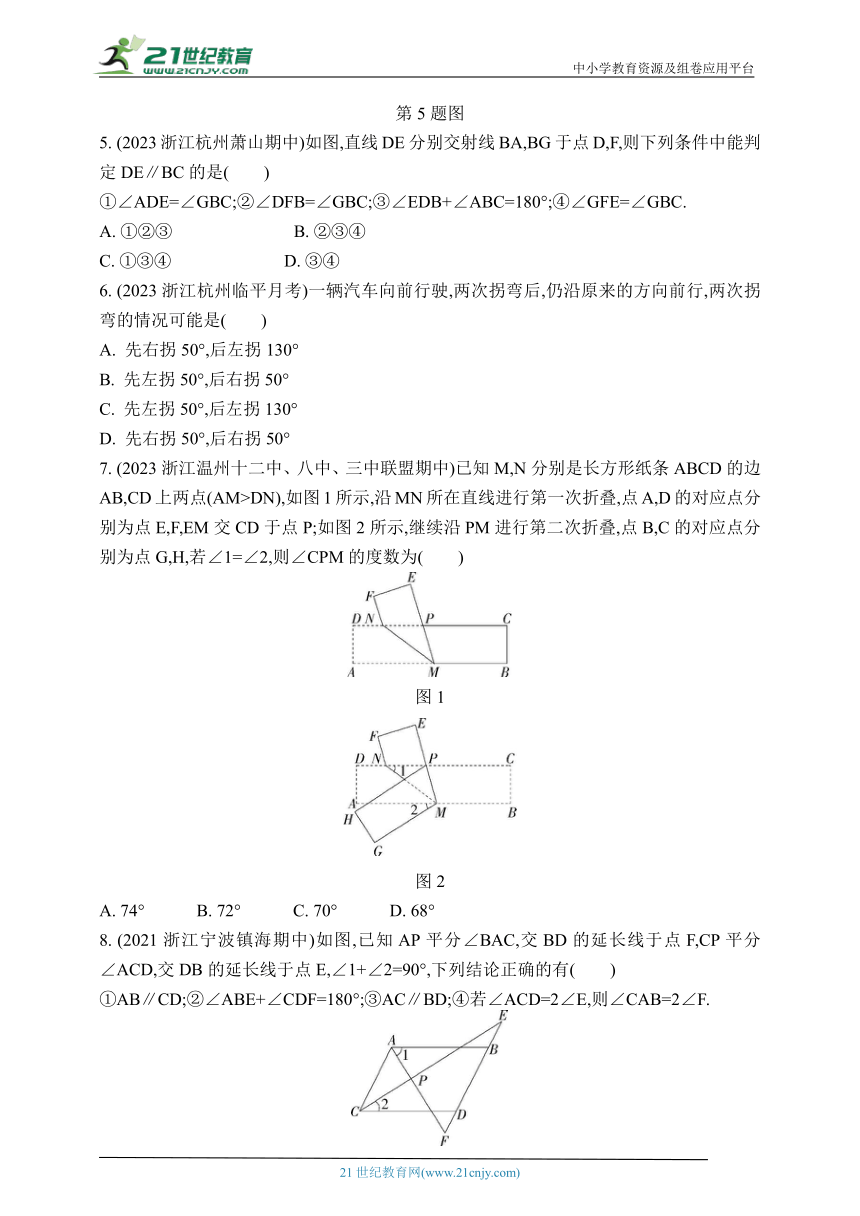
1. 【新考法】据说中国最早的风筝是由古代哲学家墨翟制作的.如图,风筝的骨架构成了多种位置关系的角.下列角中与∠1是同位角的是( )
A. ∠2 B. ∠3 C. ∠4 D. ∠5
2. (2023浙江金华义乌期中)如图,下列四个图形中,能由原图经过平移得到的图形是( )
A B C D
3. 若P,Q是直线AB外互不重合的两点,则下列说法不正确的是( )
A. 直线PQ可能与直线AB垂直
B. 直线PQ可能与直线AB平行
C. 过点P的直线一定能与直线AB相交
D. 过点Q只能画出一条直线与直线AB平行
4. (2023浙江温州期中)如图,△ABC以每秒2 cm的速度沿着射线BC向右平移,平移2秒后得到△DEF,如果AD=2CE,那么BC的长是( )
A. 4 cm B. 6 cm
C. 8 cm D. 9 cm
第4题图
第5题图
5. (2023浙江杭州萧山期中)如图,直线DE分别交射线BA,BG于点D,F,则下列条件中能判定DE∥BC的是( )
①∠ADE=∠GBC;②∠DFB=∠GBC;③∠EDB+∠ABC=180°;④∠GFE=∠GBC.
A. ①②③ B. ②③④
C. ①③④ D. ③④
6. (2023浙江杭州临平月考)一辆汽车向前行驶,两次拐弯后,仍沿原来的方向前行,两次拐弯的情况可能是( )
A. 先右拐50°,后左拐130°
B. 先左拐50°,后右拐50°
C. 先左拐50°,后左拐130°
D. 先右拐50°,后右拐50°
7. (2023浙江温州十二中、八中、三中联盟期中)已知M,N分别是长方形纸条ABCD的边AB,CD上两点(AM>DN),如图1所示,沿MN所在直线进行第一次折叠,点A,D的对应点分别为点E,F,EM交CD于点P;如图2所示,继续沿PM进行第二次折叠,点B,C的对应点分别为点G,H,若∠1=∠2,则∠CPM的度数为( )
图1
图2
A. 74° B. 72° C. 70° D. 68°
8. (2021浙江宁波镇海期中)如图,已知AP平分∠BAC,交BD的延长线于点F,CP平分∠ACD,交DB的延长线于点E,∠1+∠2=90°,下列结论正确的有( )
①AB∥CD;②∠ABE+∠CDF=180°;③AC∥BD;④若∠ACD=2∠E,则∠CAB=2∠F.
A. 1个 B. 2个
C. 3个 D. 4个
二、填空题(每小题4分,共24分)
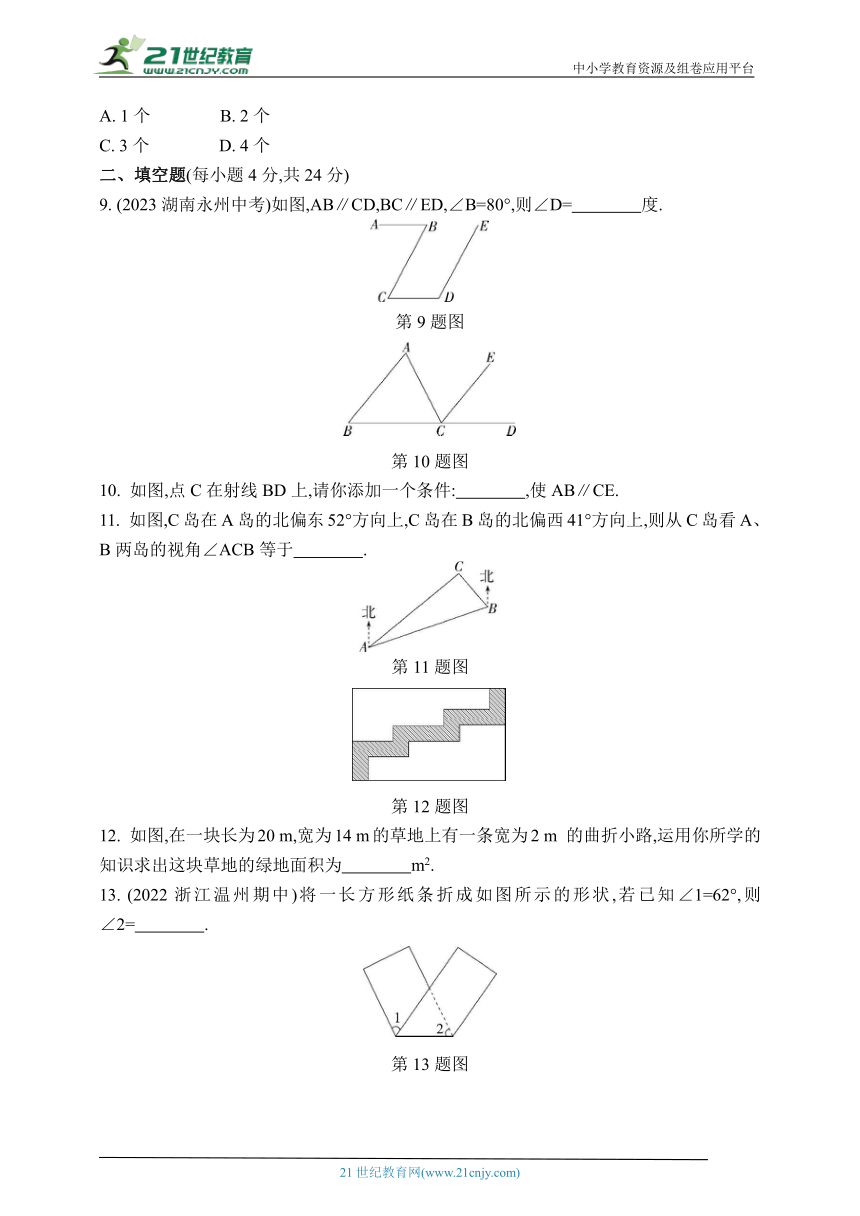
9. (2023湖南永州中考)如图,AB∥CD,BC∥ED,∠B=80°,则∠D= 度.
第9题图
第10题图
10. 如图,点C在射线BD上,请你添加一个条件: ,使AB∥CE.
11. 如图,C岛在A岛的北偏东52°方向上,C岛在B岛的北偏西41°方向上,则从C岛看A、B两岛的视角∠ACB等于 .
第11题图
第12题图
12. 如图,在一块长为20 m,宽为14 m的草地上有一条宽为2 m 的曲折小路,运用你所学的知识求出这块草地的绿地面积为 m2.
13. (2022浙江温州期中)将一长方形纸条折成如图所示的形状,若已知∠1=62°,则∠2= .
第13题图
第14题图
14. (2023浙江杭州拱墅期中)如图,已知AB∥CD∥EF,则∠1,∠2,∠3之间的数量关系是 .
三、解答题(共52分)
15. (2023浙江宁波期末)(6分)如图,AD⊥BE,BC⊥BE,∠A=∠C,点C,D,E在同一条直线上.
(1)请说明AB与CD平行;
(2)若∠ABC=110°,求∠E的度数.
16. (2023浙江宁波镇海期末)(8分)如图,已知∠1=∠C,EF⊥BC,∠2+∠3=180°.
(1)求证:∠2=∠4;
(2)试求出∠ADC的度数.
17. (2023浙江杭州期中改编)(8分)如图,AB∥CD,连结AC、BC、BD,且BD⊥BC.
(1)若∠ABC=40°,求∠BDC的度数;
(2)若∠A=2∠BDC,求证:∠ABC=∠ACB;
(3)若∠BDC与∠A互补,直接写出∠ABC与∠ACB的数量关系.
18. 【项目式学习试题】(2023浙江宁波余姚期中)(8分)【感知】已知:如图①,点E在AB上,且CE平分∠ACD,∠1=∠2.求证:AB∥CD.
将下列证明过程补充完整:
证明:∵CE平分∠ACD(已知),
∴∠2=∠ (角平分线的定义),
∵∠1=∠2(已知),
∴∠1=∠ (等量代换),
∴AB∥CD( ).
【探究】已知:如图②,点E在AB上,且CE平分∠ACD,AB∥CD.求证:∠1=∠2.
【应用】如图③,BE平分∠DBC,点A是BD上一点,过点A作AE∥BC交BE于点E,∠ABC∶∠BAE=4∶5,求∠E的度数.
图①
图②
图③
19. (10分)如图所示的是北斗七星的示意图,将北斗七星分别标为A,B,G,C,D,E,F,将A,B,G,C,D,E,F顺次连结,连结AF,已知AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=∠E=105°.
(1)求∠F的度数.
(2)∠B-∠CGF= 度.(直接写出结果)
(3)连结AD,当∠ADE与∠CGF满足怎样的数量关系时,BC∥AD 请说明理由.
20. (2023浙江湖州吴兴期中)(12分)已知:AB∥CD,E、G是AB上的点,F、H是CD上的点,∠1=∠2.
(1)如图1,求证:EF∥GH;
(2)如图2,过F点作FM⊥GH的交GH的延长线于点M,作∠BEF、∠DFM的平分线交于点N,EN交GH于点P,求证:∠N=45°;
(3)如图3,在(2)的条件下,作∠AGH的平分线交CD于点Q,若3∠FEN=4∠HFM,直接写出的值.
图1 图2 图3
答案全解全析
第1章·素养综合检测卷
答案 速查 1 2 3 4 5 6 7 8
A A C B B B B C
1. A 本题把风筝的骨架抽象成了几何图形.由题图可得,∠1与∠2构成“F”形,是同位角.故选A.
2. A 由平移的性质知,能由原图经过平移得到的图形是选项A中的图形,故选A.
3. C 直线PQ与直线AB可能平行,也可能垂直,过直线外一点有且只有一条直线与已知直线平行,故A、B、D中说法均正确,过点P的直线不一定能与直线AB相交,故C中说法错误,故选C.
4. B ∵△ABC以每秒2 cm的速度沿着射线BC向右平移,∴AD=BE=2×2=4(cm),∵AD=2CE,∴CE=2 cm,∴BC=BE+CE=4+2=6(cm),故选B.
5. B ①当∠ADE=∠GBC时,不能判定DE∥BC;②当∠DFB=∠GBC时,由内错角相等,两直线平行得DE∥BC;③当∠EDB+∠ABC=180°时,由同旁内角互补,两直线平行得DE∥BC;④当∠GFE=∠GBC时,由同位角相等,两直线平行得DE∥BC.综上,能判定DE∥BC的有②③④.故选B.
B 如图所示,∵两次拐弯后,仍沿原来的方向前行,∴AB∥DF,∴两次拐弯的情况可能是先左拐50°,后右拐50°.故选B.
7. B 由折叠的性质得,∠AMN=∠NMP,∠CPM=∠HPM,
∵AB∥CD,∴∠AMN=∠1,∴∠AMP=2∠1,
∵∠1=∠2,∴∠GMP=3∠1,
∵HP∥GM,∴∠HPM+∠GMP=180°,
即∠HPM+3∠1=180°,
∵CP∥BM,∴∠CPM=∠AMP=2∠1,
∴∠HPM=∠CPM=2∠1,∴2∠1+3∠1=180°,
∴∠1=36°,∴∠CPM=2∠1=72°.故选B.
8. C ∵AP平分∠BAC,CP平分∠ACD,
∴∠BAC=2∠1,∠ACD=2∠2,
∵∠1+∠2=90°,
∴∠BAC+∠ACD=2(∠1+∠2)=2×90°=180°,
∴AB∥CD,故①正确;
∵AB∥CD,∴∠CDF=∠ABD,
∵∠ABD+∠ABE=180°,
∴∠ABE+∠CDF=180°,故②正确;
∵∠ACD=2∠ACE,∠ACD=2∠E,
∴∠ACE=∠E,∴AC∥EF,∴∠CAF=∠F,
∵∠CAB=2∠CAF,∴∠CAB=2∠F,故④正确;
根据已知条件不能得出AC∥BD,故③错误.
故正确的结论有①②④,共3个,故选C.
9. 答案 100
解析 ∵AB∥CD,∠B=80°,∴∠BCD=∠B=80°,
∵BC∥ED,∴∠D+∠BCD=180°,∴∠D=100°.
10. 答案 ∠B=∠ECD(或∠B+∠BCE=180°或∠A=∠ACE)
解析 当∠B=∠ECD时,AB∥CE;
当∠B+∠BCE=180°时,AB∥CE;
当∠A=∠ACE时,AB∥CE.
故答案为∠B=∠ECD或∠B+∠BCE=180°或∠A=∠ACE.
11. 答案 93°
解析 如图,过点C作CE∥AF,∵AF∥BD,∴CE∥AF∥BD,∴∠1=∠CAF=52°,∠2=∠DBC=41°,
∴∠ACB=∠1+∠2=52°+41°=93°.
12. 答案 216
解析 将小路平移可得,绿地面积与长为20-2=18 m,宽为14-2=12 m的长方形的面积相等,
故绿地面积为18×12=216(m2).
13. 答案 59°
解析 如图,延长AB至点G,
由题易知,AB∥CD,
∴∠1+∠FBC+∠2=180°,∠2=∠CBG,
由翻折可知,∠CBG=∠CBF,∴2∠2+∠1=180°,
∵∠1=62°,∴∠2=×(180°-62°)=59°.
14. 答案 ∠1+∠2-∠3=180°
解析 ∵CD∥EF,∴∠2+∠CEF=180°,
∵AB∥EF,∴∠1=∠3+∠CEF,
∴∠CEF=∠1-∠3,∴∠2+∠1-∠3=180°,
即∠1+∠2-∠3=180°.
15. 解析 (1)证明:∵AD⊥BE,BC⊥BE,
∴AD∥BC,∴∠ADE=∠C.
∵∠A=∠C,∴∠ADE=∠A,
∴AB∥CD.
(2)∵∠ABC=110°,∠EBC=90°,
∴∠ABE=∠ABC-∠EBC=110°-90°=20°,
由(1)知AB∥CD,∴∠E=∠ABE=20°.
16. 解析 (1)证明:∵∠1=∠C,∴DP∥AC,
∴∠2=∠4.
(2)∵EF⊥BC,∴∠EFC=90°,
∵∠2=∠4,∠2+∠3=180°,∴∠3+∠4=180°,
∴AD∥EF,∴∠ADC=∠EFC=90°.
17. 解析 (1)∵BD⊥BC,∴∠CBD=90°,
∵∠ABC=40°,∴∠ABD=∠CBD+∠ABC=90°+40°=130°,∵AB∥CD,∴∠ABD+∠BDC=180°,
∴∠BDC=180°-∠ABD=180°-130°=50°.
(2)证明:∵AB∥CD,∴∠ABD+∠BDC=180°,∠A+∠ACD=180°,
∵∠CBD=90°,∴∠BDC=90°-∠ABC,
∵∠A=2∠BDC,
∴180°-∠BCD-∠ACB=2×(90°-∠ABC),
∵AB∥CD,∴∠ABC=∠BCD,
∴180°-∠ABC-∠ACB=180°-2∠ABC,
∴∠ABC=∠ACB.
(3)2∠ABC+∠ACB=90°.
提示:∵∠BDC与∠A互补,∴∠BDC+∠A=180°,∵∠BDC=90°-∠ABC,∠A=180°-∠ABC-∠ACB,∴90°-∠ABC+∠180°-∠ABC-∠ACB=180°,
∴2∠ABC+∠ACB=90°.
18. 解析 【感知】DCE;DCE;内错角相等,两直线平行.
【探究】证明:∵CE平分∠ACD,∴∠2=∠DCE,
∵AB∥CD,∴∠1=∠DCE,∴∠1=∠2.
【应用】∵AE∥BC,
∴∠ABC+∠BAE=180°,∠E=∠CBE,
∵∠ABC∶∠BAE=4∶5,∴∠ABC=80°,
∵BE平分∠DBC,∴∠ABE=∠CBE,
∴∠CBE=40°,∴∠E=∠CBE=40°.
19. 解析 (1)∵AF∥DE,∴∠F+∠E=180°,
∵∠E=105°,∴∠F=180°-105°=75°.
(2)115.
提示:过点C作CH∥DE,∵AF∥DE,∴CH∥AF.
∵CH∥DE,∠D=105°,∴∠DCH=∠D=105°,
∵CH∥AF,∴∠HCG=∠CGF,
∵∠B=∠GCD+10°,∴∠B=∠HCG+∠DCH+10°=∠CGF+105°+10°=∠CGF+115°,
∴∠B-∠CGF=115°.
(3)当∠ADE+∠CGF=180°时,BC∥AD.
理由:如图,∵AF∥DE,∴∠GAD+∠ADE=180°,
∵∠ADE+∠CGF=180°,∴∠GAD=∠CGF,
∴BC∥AD.
20. 解析 (1)证明:∵AB∥CD,∴∠2=∠AEF,
∵∠1=∠2,∴∠1=∠AEF,∴EF∥GH.
(2)证明:如图,过点N作NK∥CD,
∴KN∥CD∥AB,
∴∠KNE=∠BEN,
∠FNK=∠DFN,
设∠BEN=x,∠DFN=y,
∵EN、FN分别平分∠BEF、∠DFM,
∴∠ENK=∠FEN=∠BEN=x,∠FNK=∠MFN=∠DFN=y,∵AB∥CD,∴∠EFD=180°-2x,
∵FM⊥GH,∴∠FMG=90°,
∵EF∥GH,∴∠EFM=90°,
∴180°-2x+2y=90°,∴x-y=45°,
∴∠ENF=∠ENK-∠FNK=x-y=45°.
(3)=.
提示:∵3∠FEN=4∠HFM,即3x=4×2y,
∴x=y,∴x-y=y-y=45°,∴y=27°,x=72°,
∵EF∥GH,
∴∠FEG+∠EGH=180°,∠MPN=∠FEN=x=72°,
∵EN、GQ分别是∠FEG、∠EGH的平分线,
∴∠NEG+∠EGQ=90°,∴GQ⊥EN,
∵AB∥CD,∴∠GQH=∠EGQ=180°-90°-72°=18°,
∴==.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024浙教版数学七年级下册
第1章·素养综合检测卷
(考查范围:平行线 时间:60分钟 满分:100分)
题序 一 二 三 评卷人 总分
得分
一、选择题(每小题3分,共24分)
1. 【新考法】据说中国最早的风筝是由古代哲学家墨翟制作的.如图,风筝的骨架构成了多种位置关系的角.下列角中与∠1是同位角的是( )
A. ∠2 B. ∠3 C. ∠4 D. ∠5
2. (2023浙江金华义乌期中)如图,下列四个图形中,能由原图经过平移得到的图形是( )
A B C D
3. 若P,Q是直线AB外互不重合的两点,则下列说法不正确的是( )
A. 直线PQ可能与直线AB垂直
B. 直线PQ可能与直线AB平行
C. 过点P的直线一定能与直线AB相交
D. 过点Q只能画出一条直线与直线AB平行
4. (2023浙江温州期中)如图,△ABC以每秒2 cm的速度沿着射线BC向右平移,平移2秒后得到△DEF,如果AD=2CE,那么BC的长是( )
A. 4 cm B. 6 cm
C. 8 cm D. 9 cm
第4题图
第5题图
5. (2023浙江杭州萧山期中)如图,直线DE分别交射线BA,BG于点D,F,则下列条件中能判定DE∥BC的是( )
①∠ADE=∠GBC;②∠DFB=∠GBC;③∠EDB+∠ABC=180°;④∠GFE=∠GBC.
A. ①②③ B. ②③④
C. ①③④ D. ③④
6. (2023浙江杭州临平月考)一辆汽车向前行驶,两次拐弯后,仍沿原来的方向前行,两次拐弯的情况可能是( )
A. 先右拐50°,后左拐130°
B. 先左拐50°,后右拐50°
C. 先左拐50°,后左拐130°
D. 先右拐50°,后右拐50°
7. (2023浙江温州十二中、八中、三中联盟期中)已知M,N分别是长方形纸条ABCD的边AB,CD上两点(AM>DN),如图1所示,沿MN所在直线进行第一次折叠,点A,D的对应点分别为点E,F,EM交CD于点P;如图2所示,继续沿PM进行第二次折叠,点B,C的对应点分别为点G,H,若∠1=∠2,则∠CPM的度数为( )
图1
图2
A. 74° B. 72° C. 70° D. 68°
8. (2021浙江宁波镇海期中)如图,已知AP平分∠BAC,交BD的延长线于点F,CP平分∠ACD,交DB的延长线于点E,∠1+∠2=90°,下列结论正确的有( )
①AB∥CD;②∠ABE+∠CDF=180°;③AC∥BD;④若∠ACD=2∠E,则∠CAB=2∠F.
A. 1个 B. 2个
C. 3个 D. 4个
二、填空题(每小题4分,共24分)
9. (2023湖南永州中考)如图,AB∥CD,BC∥ED,∠B=80°,则∠D= 度.
第9题图
第10题图
10. 如图,点C在射线BD上,请你添加一个条件: ,使AB∥CE.
11. 如图,C岛在A岛的北偏东52°方向上,C岛在B岛的北偏西41°方向上,则从C岛看A、B两岛的视角∠ACB等于 .
第11题图
第12题图
12. 如图,在一块长为20 m,宽为14 m的草地上有一条宽为2 m 的曲折小路,运用你所学的知识求出这块草地的绿地面积为 m2.
13. (2022浙江温州期中)将一长方形纸条折成如图所示的形状,若已知∠1=62°,则∠2= .
第13题图
第14题图
14. (2023浙江杭州拱墅期中)如图,已知AB∥CD∥EF,则∠1,∠2,∠3之间的数量关系是 .
三、解答题(共52分)
15. (2023浙江宁波期末)(6分)如图,AD⊥BE,BC⊥BE,∠A=∠C,点C,D,E在同一条直线上.
(1)请说明AB与CD平行;
(2)若∠ABC=110°,求∠E的度数.
16. (2023浙江宁波镇海期末)(8分)如图,已知∠1=∠C,EF⊥BC,∠2+∠3=180°.
(1)求证:∠2=∠4;
(2)试求出∠ADC的度数.
17. (2023浙江杭州期中改编)(8分)如图,AB∥CD,连结AC、BC、BD,且BD⊥BC.
(1)若∠ABC=40°,求∠BDC的度数;
(2)若∠A=2∠BDC,求证:∠ABC=∠ACB;
(3)若∠BDC与∠A互补,直接写出∠ABC与∠ACB的数量关系.
18. 【项目式学习试题】(2023浙江宁波余姚期中)(8分)【感知】已知:如图①,点E在AB上,且CE平分∠ACD,∠1=∠2.求证:AB∥CD.
将下列证明过程补充完整:
证明:∵CE平分∠ACD(已知),
∴∠2=∠ (角平分线的定义),
∵∠1=∠2(已知),
∴∠1=∠ (等量代换),
∴AB∥CD( ).
【探究】已知:如图②,点E在AB上,且CE平分∠ACD,AB∥CD.求证:∠1=∠2.
【应用】如图③,BE平分∠DBC,点A是BD上一点,过点A作AE∥BC交BE于点E,∠ABC∶∠BAE=4∶5,求∠E的度数.
图①
图②
图③
19. (10分)如图所示的是北斗七星的示意图,将北斗七星分别标为A,B,G,C,D,E,F,将A,B,G,C,D,E,F顺次连结,连结AF,已知AF恰好经过点G,且AF∥DE,∠B=∠C+10°,∠D=∠E=105°.
(1)求∠F的度数.
(2)∠B-∠CGF= 度.(直接写出结果)
(3)连结AD,当∠ADE与∠CGF满足怎样的数量关系时,BC∥AD 请说明理由.
20. (2023浙江湖州吴兴期中)(12分)已知:AB∥CD,E、G是AB上的点,F、H是CD上的点,∠1=∠2.
(1)如图1,求证:EF∥GH;
(2)如图2,过F点作FM⊥GH的交GH的延长线于点M,作∠BEF、∠DFM的平分线交于点N,EN交GH于点P,求证:∠N=45°;
(3)如图3,在(2)的条件下,作∠AGH的平分线交CD于点Q,若3∠FEN=4∠HFM,直接写出的值.
图1 图2 图3
答案全解全析
第1章·素养综合检测卷
答案 速查 1 2 3 4 5 6 7 8
A A C B B B B C
1. A 本题把风筝的骨架抽象成了几何图形.由题图可得,∠1与∠2构成“F”形,是同位角.故选A.
2. A 由平移的性质知,能由原图经过平移得到的图形是选项A中的图形,故选A.
3. C 直线PQ与直线AB可能平行,也可能垂直,过直线外一点有且只有一条直线与已知直线平行,故A、B、D中说法均正确,过点P的直线不一定能与直线AB相交,故C中说法错误,故选C.
4. B ∵△ABC以每秒2 cm的速度沿着射线BC向右平移,∴AD=BE=2×2=4(cm),∵AD=2CE,∴CE=2 cm,∴BC=BE+CE=4+2=6(cm),故选B.
5. B ①当∠ADE=∠GBC时,不能判定DE∥BC;②当∠DFB=∠GBC时,由内错角相等,两直线平行得DE∥BC;③当∠EDB+∠ABC=180°时,由同旁内角互补,两直线平行得DE∥BC;④当∠GFE=∠GBC时,由同位角相等,两直线平行得DE∥BC.综上,能判定DE∥BC的有②③④.故选B.
B 如图所示,∵两次拐弯后,仍沿原来的方向前行,∴AB∥DF,∴两次拐弯的情况可能是先左拐50°,后右拐50°.故选B.
7. B 由折叠的性质得,∠AMN=∠NMP,∠CPM=∠HPM,
∵AB∥CD,∴∠AMN=∠1,∴∠AMP=2∠1,
∵∠1=∠2,∴∠GMP=3∠1,
∵HP∥GM,∴∠HPM+∠GMP=180°,
即∠HPM+3∠1=180°,
∵CP∥BM,∴∠CPM=∠AMP=2∠1,
∴∠HPM=∠CPM=2∠1,∴2∠1+3∠1=180°,
∴∠1=36°,∴∠CPM=2∠1=72°.故选B.
8. C ∵AP平分∠BAC,CP平分∠ACD,
∴∠BAC=2∠1,∠ACD=2∠2,
∵∠1+∠2=90°,
∴∠BAC+∠ACD=2(∠1+∠2)=2×90°=180°,
∴AB∥CD,故①正确;
∵AB∥CD,∴∠CDF=∠ABD,
∵∠ABD+∠ABE=180°,
∴∠ABE+∠CDF=180°,故②正确;
∵∠ACD=2∠ACE,∠ACD=2∠E,
∴∠ACE=∠E,∴AC∥EF,∴∠CAF=∠F,
∵∠CAB=2∠CAF,∴∠CAB=2∠F,故④正确;
根据已知条件不能得出AC∥BD,故③错误.
故正确的结论有①②④,共3个,故选C.
9. 答案 100
解析 ∵AB∥CD,∠B=80°,∴∠BCD=∠B=80°,
∵BC∥ED,∴∠D+∠BCD=180°,∴∠D=100°.
10. 答案 ∠B=∠ECD(或∠B+∠BCE=180°或∠A=∠ACE)
解析 当∠B=∠ECD时,AB∥CE;
当∠B+∠BCE=180°时,AB∥CE;
当∠A=∠ACE时,AB∥CE.
故答案为∠B=∠ECD或∠B+∠BCE=180°或∠A=∠ACE.
11. 答案 93°
解析 如图,过点C作CE∥AF,∵AF∥BD,∴CE∥AF∥BD,∴∠1=∠CAF=52°,∠2=∠DBC=41°,
∴∠ACB=∠1+∠2=52°+41°=93°.
12. 答案 216
解析 将小路平移可得,绿地面积与长为20-2=18 m,宽为14-2=12 m的长方形的面积相等,
故绿地面积为18×12=216(m2).
13. 答案 59°
解析 如图,延长AB至点G,
由题易知,AB∥CD,
∴∠1+∠FBC+∠2=180°,∠2=∠CBG,
由翻折可知,∠CBG=∠CBF,∴2∠2+∠1=180°,
∵∠1=62°,∴∠2=×(180°-62°)=59°.
14. 答案 ∠1+∠2-∠3=180°
解析 ∵CD∥EF,∴∠2+∠CEF=180°,
∵AB∥EF,∴∠1=∠3+∠CEF,
∴∠CEF=∠1-∠3,∴∠2+∠1-∠3=180°,
即∠1+∠2-∠3=180°.
15. 解析 (1)证明:∵AD⊥BE,BC⊥BE,
∴AD∥BC,∴∠ADE=∠C.
∵∠A=∠C,∴∠ADE=∠A,
∴AB∥CD.
(2)∵∠ABC=110°,∠EBC=90°,
∴∠ABE=∠ABC-∠EBC=110°-90°=20°,
由(1)知AB∥CD,∴∠E=∠ABE=20°.
16. 解析 (1)证明:∵∠1=∠C,∴DP∥AC,
∴∠2=∠4.
(2)∵EF⊥BC,∴∠EFC=90°,
∵∠2=∠4,∠2+∠3=180°,∴∠3+∠4=180°,
∴AD∥EF,∴∠ADC=∠EFC=90°.
17. 解析 (1)∵BD⊥BC,∴∠CBD=90°,
∵∠ABC=40°,∴∠ABD=∠CBD+∠ABC=90°+40°=130°,∵AB∥CD,∴∠ABD+∠BDC=180°,
∴∠BDC=180°-∠ABD=180°-130°=50°.
(2)证明:∵AB∥CD,∴∠ABD+∠BDC=180°,∠A+∠ACD=180°,
∵∠CBD=90°,∴∠BDC=90°-∠ABC,
∵∠A=2∠BDC,
∴180°-∠BCD-∠ACB=2×(90°-∠ABC),
∵AB∥CD,∴∠ABC=∠BCD,
∴180°-∠ABC-∠ACB=180°-2∠ABC,
∴∠ABC=∠ACB.
(3)2∠ABC+∠ACB=90°.
提示:∵∠BDC与∠A互补,∴∠BDC+∠A=180°,∵∠BDC=90°-∠ABC,∠A=180°-∠ABC-∠ACB,∴90°-∠ABC+∠180°-∠ABC-∠ACB=180°,
∴2∠ABC+∠ACB=90°.
18. 解析 【感知】DCE;DCE;内错角相等,两直线平行.
【探究】证明:∵CE平分∠ACD,∴∠2=∠DCE,
∵AB∥CD,∴∠1=∠DCE,∴∠1=∠2.
【应用】∵AE∥BC,
∴∠ABC+∠BAE=180°,∠E=∠CBE,
∵∠ABC∶∠BAE=4∶5,∴∠ABC=80°,
∵BE平分∠DBC,∴∠ABE=∠CBE,
∴∠CBE=40°,∴∠E=∠CBE=40°.
19. 解析 (1)∵AF∥DE,∴∠F+∠E=180°,
∵∠E=105°,∴∠F=180°-105°=75°.
(2)115.
提示:过点C作CH∥DE,∵AF∥DE,∴CH∥AF.
∵CH∥DE,∠D=105°,∴∠DCH=∠D=105°,
∵CH∥AF,∴∠HCG=∠CGF,
∵∠B=∠GCD+10°,∴∠B=∠HCG+∠DCH+10°=∠CGF+105°+10°=∠CGF+115°,
∴∠B-∠CGF=115°.
(3)当∠ADE+∠CGF=180°时,BC∥AD.
理由:如图,∵AF∥DE,∴∠GAD+∠ADE=180°,
∵∠ADE+∠CGF=180°,∴∠GAD=∠CGF,
∴BC∥AD.
20. 解析 (1)证明:∵AB∥CD,∴∠2=∠AEF,
∵∠1=∠2,∴∠1=∠AEF,∴EF∥GH.
(2)证明:如图,过点N作NK∥CD,
∴KN∥CD∥AB,
∴∠KNE=∠BEN,
∠FNK=∠DFN,
设∠BEN=x,∠DFN=y,
∵EN、FN分别平分∠BEF、∠DFM,
∴∠ENK=∠FEN=∠BEN=x,∠FNK=∠MFN=∠DFN=y,∵AB∥CD,∴∠EFD=180°-2x,
∵FM⊥GH,∴∠FMG=90°,
∵EF∥GH,∴∠EFM=90°,
∴180°-2x+2y=90°,∴x-y=45°,
∴∠ENF=∠ENK-∠FNK=x-y=45°.
(3)=.
提示:∵3∠FEN=4∠HFM,即3x=4×2y,
∴x=y,∴x-y=y-y=45°,∴y=27°,x=72°,
∵EF∥GH,
∴∠FEG+∠EGH=180°,∠MPN=∠FEN=x=72°,
∵EN、GQ分别是∠FEG、∠EGH的平分线,
∴∠NEG+∠EGQ=90°,∴GQ⊥EN,
∵AB∥CD,∴∠GQH=∠EGQ=180°-90°-72°=18°,
∴==.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 平行线
- 1.1平行线
- 1.2同位角、内错角、同旁内角
- 1.3平行线的判定
- 1.4平行线的性质
- 1.5图形的平移
- 第二章 二元一次方程组
- 2.1 二元一次方程
- 2.2 二元一次方程组
- 2.3 解二元一次方程组
- 2.4 二元一次方程组的应用
- 2.5 三元一次方程组及其解法(选学)
- 第三章 整式的乘除
- 3.1 同底数幂的乘法
- 3.2 单项式的乘法
- 3.3 多项式的乘法
- 3.4 乘法公式
- 3.5 整式的化简
- 3.6 同底数幂的除法
- 3.7 整式的除法
- 第四章 因式分解
- 4.1 因式分解
- 4.2 提取公因式
- 4.3 用乘法公式分解因式
- 第五章 分式
- 5.1 分式
- 5.2分式的基本性质
- 5.3 分式的乘除
- 5.4 分式的加减
- 5.5 分式方程
- 第六章 数据与统计图表
- 6.1数据的收集与整理
- 6.2条形统计图和折线统计图
- 6.3扇形统计图
- 6.4频数与频率
- 6.5频数直方图
