二元一次方程的应用

课件15张PPT。二元一次方程的应用巩固练习课1.有甲、乙两个粮食仓库储存一批粮食。若从甲仓库运出10吨粮食，则甲仓库比乙仓库多存粮食10吨；若从甲仓库运20吨粮食到乙仓库，则乙仓库存粮是甲仓库的1.25倍。求甲、乙两个仓库原来存粮各多少吨？
解：设甲仓库原来存粮x吨，乙仓库存粮y吨。
等量关系：
甲’ = 乙 + 10
乙’’ = 甲’’×1.25
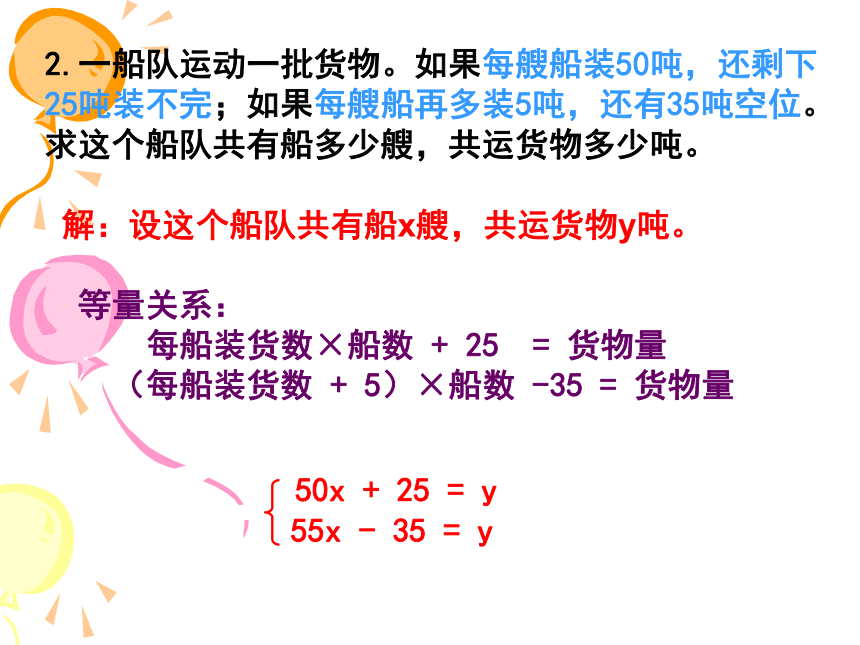
2.一船队运动一批货物。如果每艘船装50吨，还剩下25吨装不完；如果每艘船再多装5吨，还有35吨空位。求这个船队共有船多少艘，共运货物多少吨。
解：设这个船队共有船x艘，共运货物y吨。
等量关系：
每船装货数×船数 + 25 = 货物量
（每船装货数 + 5）×船数 -35 = 货物量
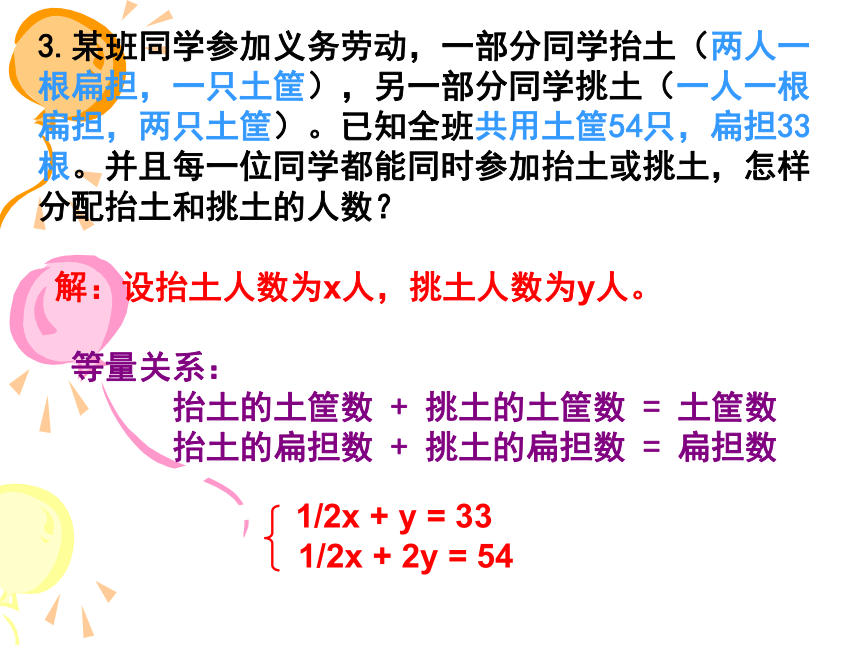
3.某班同学参加义务劳动，一部分同学抬土（两人一根扁担，一只土筐），另一部分同学挑土（一人一根扁担，两只土筐）。已知全班共用土筐54只，扁担33根。并且每一位同学都能同时参加抬土或挑土，怎样分配抬土和挑土的人数？
解：设抬土人数为x人，挑土人数为y人。
等量关系：
抬土的土筐数 + 挑土的土筐数 = 土筐数
抬土的扁担数 + 挑土的扁担数 = 扁担数
4.甲、乙两人从相距36千米的两地同时出发，相向而行，经过3小时相遇。若甲先出发2时，然后乙再出发，这样经过1时50分两人相遇。求甲、乙两人的速度。
解：设甲速为x km/h，乙速为y km/h。
等量关系：（画线段图）
甲行3小时的路程 + 乙行3小时的路程 = 36千米
甲先行2时的路程 + 甲行1时50分的路程
+ 乙行1时50分的路程 = 36千米
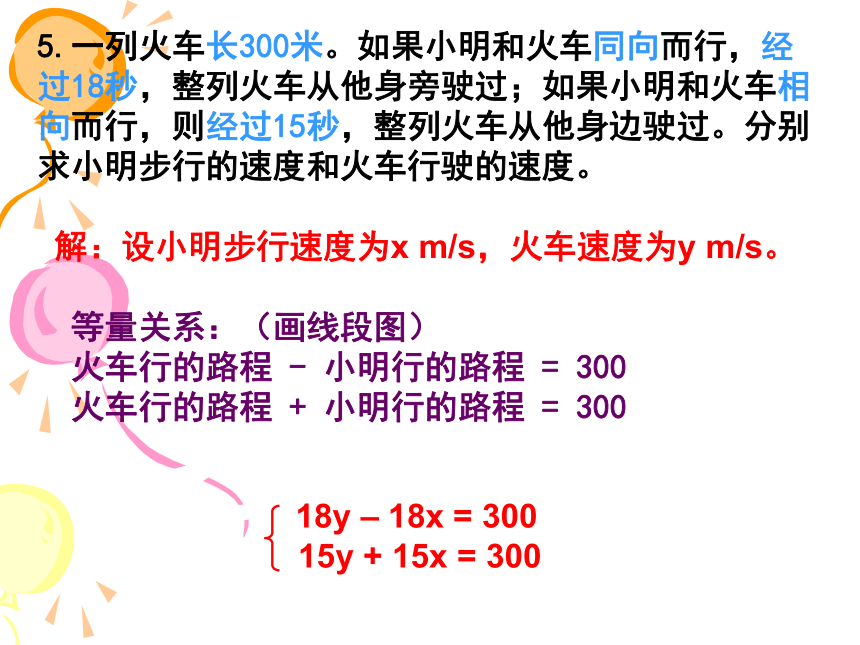
5.一列火车长300米。如果小明和火车同向而行，经过18秒，整列火车从他身旁驶过；如果小明和火车相向而行，则经过15秒，整列火车从他身边驶过。分别求小明步行的速度和火车行驶的速度。
解：设小明步行速度为x m/s，火车速度为y m/s。
等量关系：（画线段图）
火车行的路程 - 小明行的路程 = 300
火车行的路程 + 小明行的路程 = 300
6.A,B两地相距200千米，一轮船在甲、乙两地往返航行。顺流时，船航行需8时；逆流时，船航行需13时20分。求轮船在静水中航行的平均速度和水流的平均速度。
解：设轮船在静水中航行的平均速度为x km/h和水流速度为y km/h 。
等量关系：
8时×顺水速度 = 200
13时20分×逆水速度 = 200
7. 甲、乙两人同时从点A出发，沿长方形ABCD的操场四周，朝着两个不同的方向跑步（如图），经25秒，他们在CD边上的点E处相遇。已知乙的速度是甲速度的3/4，求甲、乙两人的速度和长方形操场的周长。
解：设甲速为x m/s，乙速为3/4x m/s，长方形操场周长为y m。
等量关系： （结合图形）
25秒×甲速 + 25秒×乙速 = 长方形周长
25秒×甲速 - 25秒×乙速 = 15×2
1. 小红买了单价为0.4元和0.8元的笔记本共30本，花了16元。问每种笔记本各买了多少本？
解：设单价为0.4元的笔记本买了x本，单价为0.8元的笔记本买了y本。
等量关系：
0.4元笔记本数 + 0.8元笔记本数 = 总本数30本
0.4元笔记本的价格 + 0.8元笔记本的价格 = 总价
2.设拖拉机耕地时，每时的耗油量为定值k。已知开始耕地时，油箱内有油Qo千克，则耕地t时后油箱内剩余油Q(千克）满足Q = Qo – kt。已知拖拉机耕地2时后，油箱内剩余油28千克；耕地3时后，油箱内剩余油22千克。
(1)求QO,k的值。
(2)耕地6时后，油箱内剩余油多少千克？ 解 (1) 把代入Q = Qo – kt中，得：解得(2)由(1) 得：Q = 40 - 6t
当t = 6时， Q = 40 -36 = 4
答：耕地6时后，油箱内剩余油4千克.3. 某车间有28名工人，生产一种螺栓和螺帽。已知平均每人每时能生产螺栓12个或螺帽18个，应分配多少人生产螺栓，多少人生产螺帽，才能使生产出的螺栓和螺帽刚好配套（每个螺栓配两个螺帽）？
解：设有x人生产螺栓，y人生产螺帽。
等量关系：
生产螺栓人数 + 生产螺帽人数 = 28名工人
螺栓数 ：螺帽数 = 1 ：2 4.一批机器零件共350个，甲先做2天，乙加入合作，又经过2天完成任务；如果乙先做2天，甲加入合作，需要再经过3天，完成任务，问甲乙两人每天各做多少个零件？等量关系：
甲先做的零件数 + 甲乙合作的零件数 = 350
乙先做的零件数 + 甲乙合作的零件数 = 350解：设甲每天做x个，乙做y个。5. 有两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斣，1个大桶加上5个小桶可以盛酒2斣。则1个大桶、1个小桶分别可以盛酒多少斣（斣是中国古代一种容量单位）？
解：设1个大桶可以盛酒x斣，1个小桶可以盛酒y斣。
6. 甲种矿石含铁54%，乙种矿石含铁36%，取两种矿石若干吨，混合后得到含铁48%的矿石。如果混合时，甲种矿石比原来少取12吨，乙种矿石比原来多取10吨，那么混合后的矿石含铁45%。问原来混合时，各种矿石各取多少吨？
解：设原来混合时，甲取x吨，乙取y吨。
等量关系：根据含铁量一定。 7. 某中学新建了一栋4层的教学大楼，每层楼有8间教室，进出这栋大楼共有4道门，其中两道正门大小相同。两道侧门大小也相同。安全检查时，对4道门进行了测试，发现：当同时开启一道正门和两道侧门时，2分内可以通过560名学生；当同时开启一道正门和一道侧门时，4分内可以通过800名学生。
(1)求平均每分一道正门和一道侧门各可通过多少学生；
(2)检查中发现，紧急情况时，因学生拥挤，出门的效率将降低20%。安全规定，在紧急情况下全大楼的学生应在5分内通过着4道门安全撤离。假设这栋教学大楼每间教室最多有45名学生，问这4道门是否符合安全规定？请说明理由。